7.2. Modélisation des vibrations d'une cloche : calcul des modes propres et réponse à un choc
7.2.1. Descriptif
Une cloche est étudiée à l'aide d'éléments massif quadratique.
Extrait du script Cast3M : Données, maillage et modélisation
1************************************************************************
2* REPONSE VIBRATOIRE D'UNE CLOCHE
3*
4* Calcul modal et integration temporelle suite a un choc
5* Modele 3D, elements massifs
6* Vue de la generatrice
7*
8* Z ^
9* | blocage
10* | |
11* | V
12* | +---___
13* | \
14* | |
15* | |
16* | |
17* | |
18* | |
19* | |
20* | |
21* | choc-->\
22* | \
23* +================+------> X
24* p1
25*
26* Auteur : Benoit Prabel, 2017-11-15 pour sujet de Master 2 UPMC
27* remis en forme le 2021-09-13
28* Geometrie de cloche fournie par Jose Antunes et al.
29*
30************************************************************************
31
32
33************************************************************************
34* OPTIONS
35************************************************************************
36
37* VIBR : nombre de mode et ordre de grandeur des 1eres frequences
38 Nmode = 30; Fgoal = 1000.;
39
40* DYNAMIC : SUR BASE MODALE OU ELEMENTS FINIS ?
41 ifPJBA1 = FAUX;
42* ifPJBA1 = VRAI;
43
44* TRAC et DESS : OPTIONS
45 OPTI 'TRAC' 'PSC' 'EPTR' 5 'POTR' 'HELVETICA_16' ;
46
47
48************************************************************************
49* MODELISATION
50************************************************************************
51
52* RECUPERATION DU MAILLAGE
53 OPTI REST 'mesh_bell.xdr';
54 REST ;
55* TRACE DU MAILLAGE
56 MESS '>>> Le maillage comporte ' (NBEL Vbell) ' elements quadratiques';
57* TRAC Vbell 'FACE';
58
59* DONNEES MATERIAU
60* Ey1 : module d'Young
61* nu1 : coefficient de poisson
62* ro1 : densite
63* al1 : coefficient de dilatation thermique (inutile ici)
64 Ey1 = 100.E9;
65 nu1 = 0.34;
66 ro1 = 8910.;
67 al1 = 15.E-6;
68
69* MODELE et MATERIAU
70 modbell = MODE Vbell 'MECANIQUE' 'ELASTIQUE' 'ISOTROPE';
71 matbell = MATE modbell 'YOUN' Ey1 'NU' nu1 'RHO' ro1 'ALPH' al1;
72
73* MATRICES
74 K1 = RIGI modbell matbell;
75 M1 = MASS modbell matbell;
76
77* CONDITIONS AUX LIMITES
78 CL1 = BLOQ Senca 'DEPL';
79 Ktot1 = K1 et CL1;
7.2.2. Calcul des modes réels
On calcule les 30 premiers modes propres réels de la structure, ce qui permet de couvrir la plage 0 - 4000 Hz.
Extrait du script Cast3M : Calcul des modes réels
81************************************************************************
82* ANALYSE MODALE
83************************************************************************
84
85* CALCUL DES MODES
86* Tmode = VIBR 'IRAM' Fgoal Nmode Ktot1 M1 ;
87 Tmode = VIBR 'SIMUL' Fgoal Nmode Ktot1 M1 ;
88
89* POST TRAITEMENT : preparation
90* trace de face et de dessus
91 eye_y = 0. -1.2E6 0. ;
92 eye_z = 0. 0. 1.2E6;
93* petit travail car on veut tracer seulement qq aretes visibles
94 are_bell = ARET Vbell;
95 env_Sbell = CONT Sbell;
96 env_trac = c_bas ET env_Sbell;
97 prTOUR = PROG 90. 180. 270.;
98 REPE BTOUR (DIME prTOUR);
99 angTOUR = EXTR prTOUR &BTOUR;
100 env_trac = env_trac ET (TOUR env_Sbell angTOUR PR1 PR2);
101 FIN BTOUR;
102 ELIM env_trac Vbell 1.E-8;
103 env_trac = env_trac et are_bell;
104 env_trac = env_trac COUL 'BRON';
105
106* POST TRAITEMENT : appel a POSTVIBR
107* table d'options de POSTVIBR
108 ToptPost = TABL;
109 ToptPost . 'MAILLAGE_2' = env_trac ;
110* en vue de face
111 OPTI 'OEIL' eye_y;
112 POSTVIBR Tmode ToptPost (MOTS 'TABL' 'DEFO' 'MAIL' 'LIST');
113* idem en vue de dessus
114 OPTI 'OEIL' eye_z;
115 POSTVIBR Tmode ToptPost (MOTS 'TABL' 'DEFO');

Quelques exemple de déformées modales \(\varphi\) en vue de face et de dessus
7.2.3. Calcul de la réponse à un choc par intégration temporelle
On simule un choc par une force de courte durée (0.1 ms). Deux intégrations temporelles sont menées avec le même pas de temps (\(\Delta t = 10\) µs) et comparées :
avec la procédure DYNAMIC, en utilisant le schéma de l'accélération moyenne et sur base éléments finis.
avec l'opérateur DYNE, en utilisant le schéma des différences centrées et sur base modale.
On observe des résultats très proches, mais une bien meilleur efficacité en utilisant DYNE, due à l'utilisation de la base réduite (diminution du nombre de ddl) et au travail en lagage compilé (fortran pour un opérateur) plutôt qu'interprété (gibiane pour une procédure).
Extrait du script Cast3M : Calcul de la réponse au balourd
119************************************************************************
120* CHARGEMENT
121************************************************************************
122
123* description spatiale
124 Pchoc1 = c_i POINT PROCH (p86);
125 Fchoc1 = FORC 'FX' 1. Pchoc1;
126
127* description temporelle
128 Tchoc = 1.E-4;
129 evolF = EVOL MANU 't' (prog 0. Tchoc (2*Tchoc) 1.)
130 '|F|'(prog 0. 1. 0. 0.);
131
132* objet chargement F(x,t) sur base physique et modale
133 CHA1 = CHAR 'MECA' Fchoc1 evolF;
134 CHA1P = PJBA CHA1 Tmode;
135
136
137************************************************************************
138* ANALYSE PAR INTEGRATION TEMPORELLE : PREPARATION
139************************************************************************
140
141* MATRICE D'AMORTISSEMENT
142
143* Si on souhaite definir directement un amortissement modal (en %) -----
144* c1pp = PROG 20. 20. (Nmode - 2)*1.;
145* C1P = AMOR Tmode c1pp ;
146
147* Si on prend un amortissement de Rayleigh tel que C = a M + b K -----
148* On se donne les contraintes :
149* |a/2w + bw/2 = 0.20 pour w=2*pi*87
150* |a/2w + bw/2 = 0.02 pour w=2*pi*1000
151 w1 = 2. * pi * (Tmode . 'MODES' . 1 . 'FREQUENCE');
152 w2 = 2. * pi * 2000.;
153 prMatrix = PROG (0.5/w1) (0.5*w1) (0.5/w2) (0.5*w2);
154 Matrix = MANU 'RIGI' PR1 (MOTS 'A' 'B') 'DUAL' (MOTS 'FA' 'FB') 'QUEL' prMatrix;
155 FAB = MANU 'CHPO' PR1 2 'FA' 0.20 'FB' 0.01;
156 UAB = RESO Matrix FAB;
157 coef_a = EXTR UAB 'A' PR1;
158 coef_b = EXTR UAB 'B' PR1;
159 prfreq = PROG 1. PAS 1. 100. PAS 10. 1000. PAS 100. 3000.;
160 prw = 2. * pi * prfreq;
161 prxi = 0.5 * ((coef_a * (prw**-1)) + (coef_b * prw));
162 evxi = EVOL 'BOUT' 'MANU' 'f (Hz)' prfreq '\x (%)' (100.*prxi);
163 dess evxi 'YBOR' 0. 20. 'YGRA' 1. 'GRIL' 'POIN' 'GRIS';
164* C = a M + b K
165 C1 = (coef_a * M1) ET (coef_b * K1);
166 C1P = PJBA C1 Tmode;
167* on peut extraire les amortissements modaux
168 prci = EXTR (EXTR C1P 'DIAG') 'VALE';
169 prwi = 2.*pi * (Tmode . 'LISTE_FREQUENCES');
170 prmi = Tmode . 'LISTE_MASSES';
171 prxi = prci / (2.*prwi * prmi);
172 list prxi;
173
174* MATRICES masse et raideur sur base modale
175 K1P = PJBA K1 Tmode;
176 M1P = PJBA M1 Tmode;
177
178* DISCRETISATION TEMPORELLE
179 tfin = 50.E-3;
180* pour l'implicite (DYNAMIC)
181 dt = 0.01E-3; nsort = 1;
182 tprog = prog 0. 'PAS' dt tfin;
183 nt = dime tprog;
184 MESS nt ' pas de temps avec dt=' dt;
185* pour DYNE, on peut se permettre un pas de temps + fin
186* xdt = 4;
187 xdt = 1;
188 dtDYNE = dt / xdt;
189 ntDYNE = (nt - 1) * xdt + 1;
190 nsortDYNE = nsort * xdt;
191* nsortDYNE = 2;
192
193* CONDITIONS INITIALES
194 U0 = CHPO 'UNIFORME' 0. M1;
195 U0_P = MANU 'CHPO' (Tmode . 'MAILLAGE_REPERE') 'ALFA' 0.;
196
197
198************************************************************************
199* ANALYSE PAR INTEGRATION TEMPORELLE 1 : via DYNE
200************************************************************************
201
202* MISE EN DONNEES POUR DYNE
203 Tamor = TABL 'AMORTISSEMENT'; Tamor . 'AMORTISSEMENT' = C1P ;
204 Tchar = TABL 'CHARGEMENT' ; Tchar . 'BASE_A' = CHA1P;
205 Tini = TABL 'INITIAL' ; Tini . 'DEPLACEMENT' = U0_P;
206 Tini . 'VITESSE' = U0_P;
207 Tsort = TABL 'SORTIE' ; Tsort . 'TYPE_SORTIE' = MOT 'LISTREEL';
208
209* INTEGRATION TEMPORELLE
210 TDYNE = DYNE 'DIFFERENCES_CENTREES' Tmode Tamor Tchar Tini Tsort
211 ntDYNE dtDYNE nsortDYNE;
212
213* POST TRAITEMENT DES RESULTATS
214* evolutions
215 ux1ev = EVOL 'BLEU' RECO 'LEGE' 'DYNE' TDYNE Tmode 'DEPL' p1 'UX';
216 vx1ev = EVOL 'BLEU' RECO 'LEGE' 'DYNE' TDYNE Tmode 'VITE' p1 'UX';
217
218* spectre de la vitesse
219 p = ENTI ( (log ntDYNE) / (log 2.) );
220 Dv1 = DSPR p vx1ev 'FMIN' 10. 'FMAX' 5000. 'BLEU';
221
222* traces
223 DESS ux1ev 'LEGE' 'NE' XBOR 0. tfin;
224 DESS vx1ev 'LEGE' 'NE' XBOR 0. tfin;
225 DESS Dv1;
226
227
228************************************************************************
229* ANALYSE PAR INTEGRATION TEMPORELLE 2 : via DYNAMIC
230************************************************************************
231* on fait la meme analyse et on verifie juste que le resultat est le meme
232
233* MISE EN DONNEES POUR DYNAMIC
234 TAB1in = TABL;
235SI ifPJBA1;
236 TAB1in . 'DEPL' = U0_P ;
237 TAB1in . 'VITE' = U0_P ;
238 TAB1in . 'CHAR' = CHA1P;
239 TAB1in . 'RIGI' = K1P ;
240 TAB1in . 'MASS' = M1P ;
241 TAB1in . 'AMOR' = C1P ;
242SINON;
243 TAB1in . 'DEPL' = U0 ;
244 TAB1in . 'VITE' = U0 ;
245 TAB1in . 'CHAR' = CHA1 ;
246 TAB1in . 'RIGI' = Ktot1;
247 TAB1in . 'MASS' = M1 ;
248 TAB1in . 'AMOR' = C1 ;
249FINSI;
250 TAB1in . 'TEMPS_CALCULES' = tprog;
251 TAB1in . 'PAS_SAUVES' = nsort;
252
253* INTEGRATION TEMPORELLE
254 TAB1 = DYNAMIC TAB1in ;
255
256* POST TRAITEMENT DES RESULTATS
257* on prepare les EVOLUTIONS TEMPORELLES :
258* temps sauves
259 tp = prog ;
260* deplacements et vitesse au point p1 selon UX pour le choc 1
261 ux2p = prog;
262 vx2p = prog;
263*------------------------ boucle sur les pas de temps
264 npas = dime TAB1;
265 ipas = 0;
266 REPE BPAS npas; ipas = ipas + 1;
267 mess 'ipas = ' ipas ;
268 SI (NON (EXIS TAB1 ipas)); ITER BPAS ; FINSI;
269* recup de la solution au pas ipas et temps t
270 t = TAB1 . ipas . 'TEMP';
271* grandeurs souhaitees
272 SI ifPJBA1;
273 u = RECO (TAB1 . ipas . 'DEPL') Tmode;
274 v = RECO (TAB1 . ipas . 'VITE') Tmode;
275* TAB1 . ipas . 'DEPL_RECO' = u;
276* TAB1 . ipas . 'VITE_RECO' = v;
277 SINON;
278 u = TAB1 . ipas . 'DEPL';
279 v = TAB1 . ipas . 'VITE';
280 FINSI;
281* stockage des grandeurs souhaitees
282 tp = tp et t;
283 ux2p = ux2p et (extr u p1 'UX');
284 vx2p = vx2p et (extr v p1 'UX');
285 FIN BPAS;
286*------------------------ fin de boucle sur les pas de temps
287
288* evolutions
289 ux2ev = EVOL 'ROSE' MANU 'LEGE' 'DYNAMIC' 't' tp 'u_{x}(p1)' ux2p;
290 vx2ev = EVOL 'ROSE' MANU 'LEGE' 'DYNAMIC' 't' tp 'v_{x}(p1)' vx2p;
291
292* spectre de la vitesse
293 p = ENTI ( (log nt) / (log 2.) );
294 Dv2 = DSPR p vx2ev 'FMIN' 10. 'FMAX' 5000. 'ROSE';
295
296* traces
297 DESS ux2ev 'LEGE' 'NE' XBOR 0. tfin;
298 DESS vx2ev 'LEGE' 'NE' XBOR 0. tfin;
299 DESS Dv2;
300
301
302************************************************************************
303* TRACES COMPARATIFS
304************************************************************************
305
306 DESS (ux2ev ET ux1ev) 'LEGE' 'NE' XBOR 0. tfin;
307 DESS (vx2ev ET vx1ev) 'LEGE' 'NE' XBOR 0. tfin;
308 dess (Dv2 ET Dv1 ) 'LEGE' 'NE' TITX 'f (Hz)' TITY 'S_{vv}';
309
310
311************************************************************************
312* SAUVEGARDE ET FIN NORMALE
313************************************************************************
314
315OPTI SAUV 'vibrations_cloche.xdr';
316SAUV;
317
318
319TEMP IMPR MAXI CPU;
320FIN ;
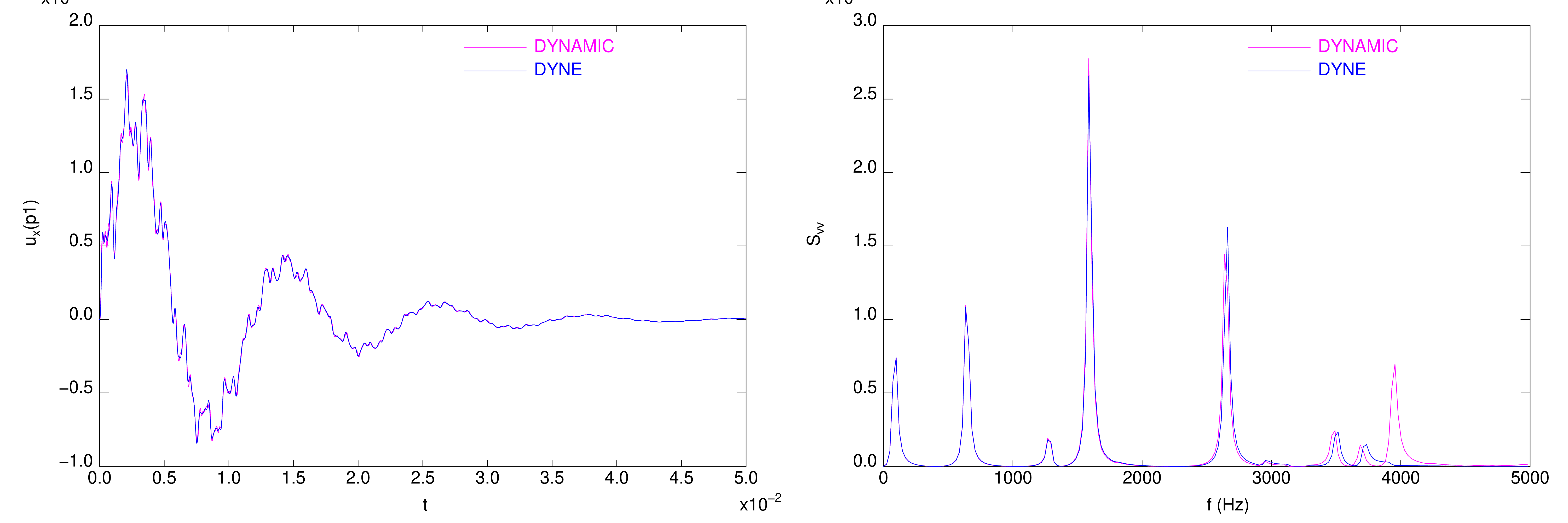
Evolution temporelle (à gauche) et densité spectrale de puissance (à droite) du déplacement en un point en bas de la cloche pour les intégrations temporelles par DYNAMIC et DYNE.