7.1. Modélisation d'un rotor de Laval : calcul des modes propres réels et complexes, réponse au balourd
7.1.1. Descriptif
Un rotor dit de Laval est étudié à l'aide d'éléments poutre de Timoshenko dans le repère fixe.
Extrait du script Cast3M : Données, maillage et modélisation
1*******************************************************************************
2* *
3* Rotor de Laval *
4* Etude dans le repere inertiel (ou fixe) avec elements poutre de TIMO *
5* *
6* p2 kpal *
7* z=L +--/\/\/\--| *
8* | *
9* | *
10* | *
11* p1a| *
12* =======+======= Mdisc, Ixyz *
13* p1b| *
14* | *
15* | *
16* | *
17* z=0 +--/\/\/\--| *
18* p0 *
19* *
20* *
21* Réf : *
22* [1] Vollan, Arne, and Louis Komzsik. "Computational techniques of rotor *
23* dynamics with the finite element method". CRC Press, 2012.] *
24* *
25* Mots-clés : Vibrations, calcul modal, machines tournantes, *
26* poutre, modes complexes, reponse frequentielle *
27* *
28* Auteur: Benoit Prabel, Mars 2020 *
29* *
30*******************************************************************************
31
32*******************************************************************************
33* OPTIONS
34*******************************************************************************
35
36* PARAMETRES : on souhaite NbModR modes
37 NbModR = 5;
38
39* dimension, type d'elements geometriques, ...
40 OPTI 'DIME' 3 'ELEM' 'SEG2';
41
42* visualisation (sortie postscript)
43 GRAPH = VRAI;
44 OPTI 'TRAC' PSC 'EPTR' 12 'POTR' 'HELVETICA_16'
45 'FTRA' (CHAI 'rotor_laval_poutre-' NbModR '.ps');
46
47
48*******************************************************************************
49* DONNEES
50*******************************************************************************
51
52* arbre (shaft)
53 L = 1.0 ;
54 Dshaft = 64.E-3;
55* Disque (disc)
56 zdisc = 0.5*L;
57 Mdisc = 40.;
58 Izdisc = 5. ;
59* Materiau
60 E1 = 2.1E11 ;
61 nu1 = 0.3 ;
62 rho1 = 7800. ;
63 Visc1= 0.00001*E1;
64* Palier
65 kpal_x = 3.9E6;
66 kpal_y = kpal_x;
67 cpal_x = 1000.;
68 cpal_y = cpal_x;
69
70* Calculs preliminaires pour completer les donnees
71
72* formule des caracteristiques des poutres a section circulaire creuse :
73* Section = pi * ((Rext**2) - (Rint**2));
74* Itorsion = pi * ((Rext**4) - (Rint**4)) / 2.;
75* Iflexion = pi * ((Rext**4) - (Rint**4)) / 4.;
76* on a un disque plein ==> Rint = 0
77* on a les donnees (Mdisc et Idisc) integrees sur h et multipliee par rho1 :
78* rho1 * h * pi * (R**2) = Mdisc
79* rho1 * h * pi/2. * (R**4) = Izdisc
80* (2)/(1) ==> 0.5*(R**2) = Izdisc/Mdisc ==> Rdisc = (2*Izdisc/Mdisc)**0.5
81 Rdisc = (2*Izdisc/Mdisc)**0.5;
82 hdisc = Mdisc / (rho1 * pi * (Rdisc**2));
83 MESS 'Rdisc=' Rdisc ' hdisc=' hdisc;
84
85* ==> caracteristiques geometriques de la poutre definissant le disque :
86 Sdisc = pi * (Rdisc**2);
87 Iz = pi/2. * (Rdisc**4);
88 Ix = pi/4. * (Rdisc**4);
89
90* caracteristique de l'arbre
91 Rshaft = Dshaft /2.;
92 Sshaft = pi * (Rshaft**2);
93 Izshaft = pi/2. * (Rshaft**4);
94 Ixshaft = pi/4. * (Rshaft**4);
95
96
97*******************************************************************************
98* MAILLAGE
99*******************************************************************************
100
101* PARAMETRES
102 OPTI 'ELEM' SEG2;
103 nL = 80;
104 nVect = nL/16;
105
106* POINTS
107 p0 = 0. 0. 0.;
108 p1a = 0. 0. (zdisc - hdisc);
109 p1b = 0. 0. (zdisc + hdisc);
110 p2 = 0. 0. L;
111* points du palier
112 ppal = p0 et p2;
113
114* DROITES
115 d1a = DROI (nL/2) p0 p1a;
116 d2 = (DROI 1 p1a p1b) COUL 'BLEU';
117 d1b = DROI (nL/2) p1b p2 ;
118 d1 = d1a et d1b;
119 dtot= d1 et d2;
120
121* TRACE
122* si GRAPH;
123* TRAC dtot 'TITRE' 'maillage';
124* finsi;
125
126* ON VEUT QUELQUES POINTS POUR LE TRACE DE VECTEUR DANS POSTVIBR
127 dVect = (DROI nVect p0 p1a) ET d2 ET (DROI nVect p1b p2);
128 pVect = CHAN dVect 'POI1';
129 ELIM dtot pVect (1.E-8*L);
130
131
132*******************************************************************************
133* MODELE, MATERIAU, MATRICES
134*******************************************************************************
135*
136* 1 : arbre
137 mod1 = MODE d1 'MECANIQUE' TIMO;
138 mat1 = MATE mod1 'YOUNG' E1 'NU' Nu1 'RHO' Rho1
139 'SECT' Sshaft 'INRY' Ixshaft 'INRZ' Ixshaft 'TORS' Izshaft
140 'OMEG' 1. 'VISQ' Visc1;
141*
142* 2 : disque
143 mod2 = MODE d2 'MECANIQUE' TIMO;
144 mat2 = MATE mod2 'YOUNG' E1 'NU' Nu1 'RHO' Rho1
145 'SECT' Sdisc 'INRY' Ix 'INRZ' Ix 'TORS' Iz
146 'OMEG' 1. 'VISQ' Visc1;
147*
148 mod12 = mod1 et mod2;
149 mat12 = mat1 et mat2;
150
151* raideur, masse, couplage gyroscopique
152 K12 = RIGI mod12 mat12;
153 Mtot = MASS mod12 mat12;
154 Gtot = GYRO mod12 mat12;
155* amortissement + amortissement corotatif
156 C12 KROT12 = AMOR mod12 mat12 'COROTATIF';
157
158* 3 : paliers
159* appuis = raideurs discretes
160 Kx3 = APPU 'UX' kpal_x ppal;
161 Ky3 = APPU 'UY' kpal_x ppal;
162 K3 = Kx3 et Ky3;
163 Cx3 = APPU 'UX' cpal_x ppal;
164 Cy3 = APPU 'UY' cpal_x ppal;
165 C3 = Cx3 et Cy3;
166
167* autres conditions aux limites ?
168 bloZ = BLOQ 'UZ' 'RZ' ppal;
169
170* assemblage
171 Ktot = K12 et K3 et bloZ;
172 Ctot = C12 et C3;
173
174
7.1.2. Calcul des modes réels
On calcule les 5 premiers modes propres réels de la structure au repos (vitesse de rotation \(\Omega = 0\)).
Extrait du script Cast3M : Calcul des modes réels
175*******************************************************************************
176* MODES REELS
177*******************************************************************************
178
179* PARAMETRES : on souhaite NbModR modes (cf. tete de fichier)
180
181* CALCUL
182 TBasR1 = VIBR 'SIMUL' 1. NbModR Ktot Mtot;
183
184* POST-TRAITEMENT
185si GRAPH;
186
187* tableau + deformees modale automatise via la procedure postvibr
188* on peux customiser avec table d'options
189 Toptions = TABL;
190 Toptions .'MAILLAGE_VECTEUR' = pVect;
191 POSTVIBR TBasR1 Toptions;
192
193* quel est ce mode 3 ?
194 phi3 = TBasR1 . 'MODES' . 3 . 'DEFORMEE_MODALE';
195 TITRE 'Mode 3 : RZ ';
196 TRAC (EXCO phi3 'RZ') dtot 'NOLE';
197* c'est de la torsion !
198* si on souhaite le supprimer, il faudrait bloquer plus de ddls RZ
199sinon;
200 POSTVIBR TBasR1 (MOTS 'TABL');
201
202finsi;
203
204* VIBR 'SIMUL' a detecte des modes doubles et il a donc ajoute un mode en plus
205* retrouvons le vrai nombre avec une mini-boucle...
206 NbModR = NbModR - 1 ;
207 REPE bb; NbModR = NbModR + 1;
208 SI (EXIS TBasR1 . 'MODES' (NbModR + 1));
209 ITER bb;
210 SINON;
211 QUIT bb;
212 FINSI;
213 FIN bb;
214 MESS 'nombre de modes reels fournis in fine par VIBR SIMUL='NbModR;
215
216
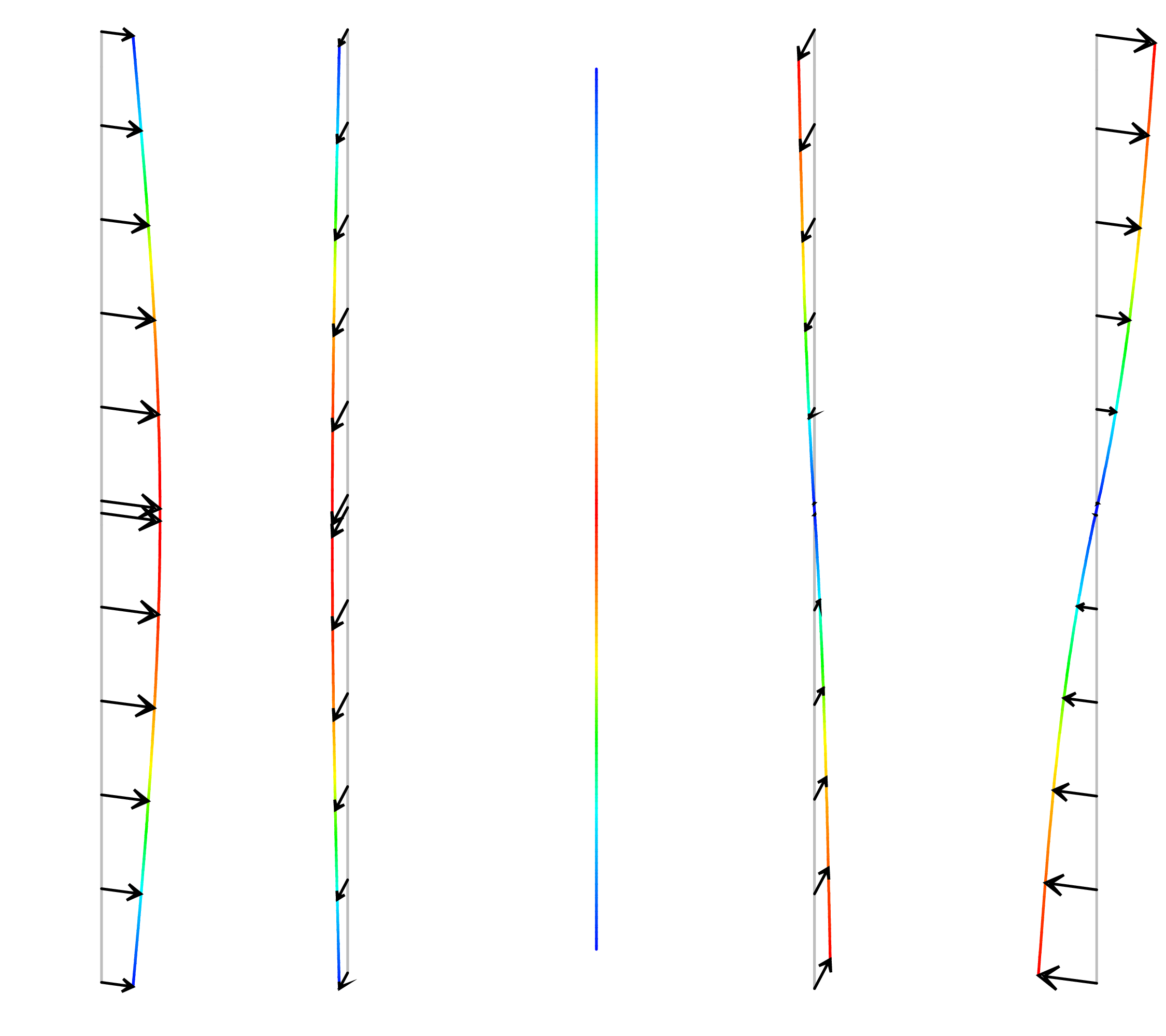
Déformées \(\varphi\) des premiers modes réels
7.1.3. Calcul du diagramme Campbell
On calcule l'évolution des modes complexes du rotor avec la vitesse de rotation \(\Omega\).
Extrait du script Cast3M : Calcul des modes complexes
217*******************************************************************************
218* CALCUL DU DIAGRAMME DE CAMPBELL
219* (= EVOLUTION DES FREQUENCES COMPLEXES AVEC LA VITESSE DE ROTATION)
220*******************************************************************************
221
222* OMEGA en RoundPerMinute
223 si (NbModR < 6);
224 PR_RPM = prog 0. 'PAS' 0.1E3 10.E3;
225 sinon;
226 PR_RPM = prog 0. 'PAS' 0.1E3 20.E3;
227 finsi;
228
229* on choisit l'unite pour OMEGA : RoundPerMinute, rad/s ou Hz(=tr/s)
230* G est calcule pour 1 rad/s --> multiplier par FAC_G
231 UNIT_OMEG = mot 'RPM' ; FAC_G = (2.*pi/60.); PROMEG = PR_RPM;
232* UNIT_OMEG = mot 'rad/s'; FAC_G = 1.; PROMEG = (2.*pi/60.) * PR_RPM ;
233* UNIT_OMEG = mot 'Hz' ; FAC_G = 2.*pi; PROMEG = PR_RPM / 60.;
234 cha_x = chai '\W ('UNIT_OMEG')';
235 NOMEG = DIME PROMEG;
236
237* PROJECTION DES MATRICES ASSEMBLEES SUR LA BASE REELLE
238 M1P = PJBA TBasR1 Mtot ;
239 G1P = PJBA TBasR1 Gtot ;
240 K1P = PJBA TBasR1 (K12 et K3) ;
241 C1P = PJBA TBasR1 Ctot;
242 KROT1P = PJBA TBasR1 KROT12;
243
244* REM : il serait possible d'utiliser directement la procedure campbell,
245* mais il semble plus pedagogique de reecrire ici la boucle et le calcul
246
247* CREATION DE 2*NbModC LISTREELS DE TAILLE NOMEG
248 NbModC = 2*NbModR;
249 TfreqR = TABL;
250 TfreqI = TABL;
251 REPE BmodC NbModC;
252 TfreqR . &BmodC = PROG NOMEG*0.;
253 TfreqI . &BmodC = PROG NOMEG*0.;
254 FIN BmodC;
255* + 2 LISTREELS TEMPORAIRES DE TRAVAIL
256 prWorkR = PROG NbModC*0.;
257 prWorkI = PROG NbModC*0.;
258
259* ON BOUCLE SUR LES FREQUENCES DE ROTATION Omega_j ---------------------
260 REPE BOMEG NOMEG;
261 Omega_j = EXTR PROMEG &BOMEG;
262 MESS 'Calcul des modes complexes pour \W=' Omega_j ' ' UNIT_OMEG;
263
264* on va resoudre : [ [K + W*C'] + iw [C + W*G] - w^2 [M] ] * \psi = 0
265* G est calcule pour 1 rad/s -> on mutliplie par FAC_G
266 K_j = K1P ET (Omega_j * KROT1P);
267 C_j = C1P ET (Omega_j * FAC_G * G1P);
268 M_j = M1P;
269 TbasC_j = VIBC M_j K_j C_j ;
270
271* extraction des frequences et tri par ordre croissant
272 SI (&BOMEG EGA 1);
273 ORDOVIBC TbasC_j;
274* puis en minimisant la distance au resultat precedent
275 SINON;
276 ORDOVIBC TbasC_j TbasC_jm1;
277 FINSI;
278 prwR_j = TbasC_j . 'LISTE_FREQUENCES_REELLES' ;
279 prwI_j = TbasC_j . 'LISTE_FREQUENCES_IMAGINAIRES' ;
280* pour le prochain pas
281 TbasC_jm1 = TbasC_j;
282
283* on stocke dans les listreels finaux
284 REPE BmodC NbModC;
285 REMP (TfreqR . &BmodC) &BOMEG (EXTR prwR_j &BmodC);
286 REMP (TfreqI . &BmodC) &BOMEG (EXTR prwI_j &BmodC);
287 FIN BmodC;
288
289 FIN BOMEG ;
290* FIN DE LA BOUCLE SUR LES FREQUENCES DE ROTATION ----------------------
291
292
293* POST-TRAITEMENT GRAPHIQUE
294* on ne trace que les modes tq wR>0 -> i ={NbModC/2+1 ... NbModC}
295 IFhalf = VRAI;
296 si IFhalf; NC = NbModC/2; ideb = NC;3
297 sinon; NC = NbModC; ideb = 0;
298 finsi;
299
300 colors = @PALETTE NC;
301 evfreqR = VIDE 'EVOLUTIO';
302 evfreqI = VIDE 'EVOLUTIO';
303 REPE BmodC NC;
304 coco = EXTR colors &BmodC;
305 i = ideb + &BmodC;
306 evfreqR = evfreqR
307 et (EVOL coco 'MANU' cha_x PROMEG 'w_{R} (Hz)' (TfreqR . i));
308 evfreqI = evfreqI
309 et (EVOL coco 'MANU' cha_x PROMEG 'w_{I} (/s)' (TfreqI . i));
310 FIN BmodC;
311
312si GRAPH;
313 TITRE 'Campbell diagram';
314 prBisRPM = PROG 0. (MAXI PROMEG);
315 evBissec1 = EVOL 'MANU' cha_x prBisRPM 'w_{R} (Hz)' (prBisRPM / 60.);
316 evBissec0 = EVOL 'MANU' cha_x prBisRPM 'w_{I} (Hz)' (0. * prBisRPM);
317 TBissec = TABL; TBissec . 1 = MOT 'TIRR';
318 DESS (evBissec1 et evfreqR) TBissec;
319 DESS (evBissec0 et evfreqI) TBissec;
320finsi;
321
322
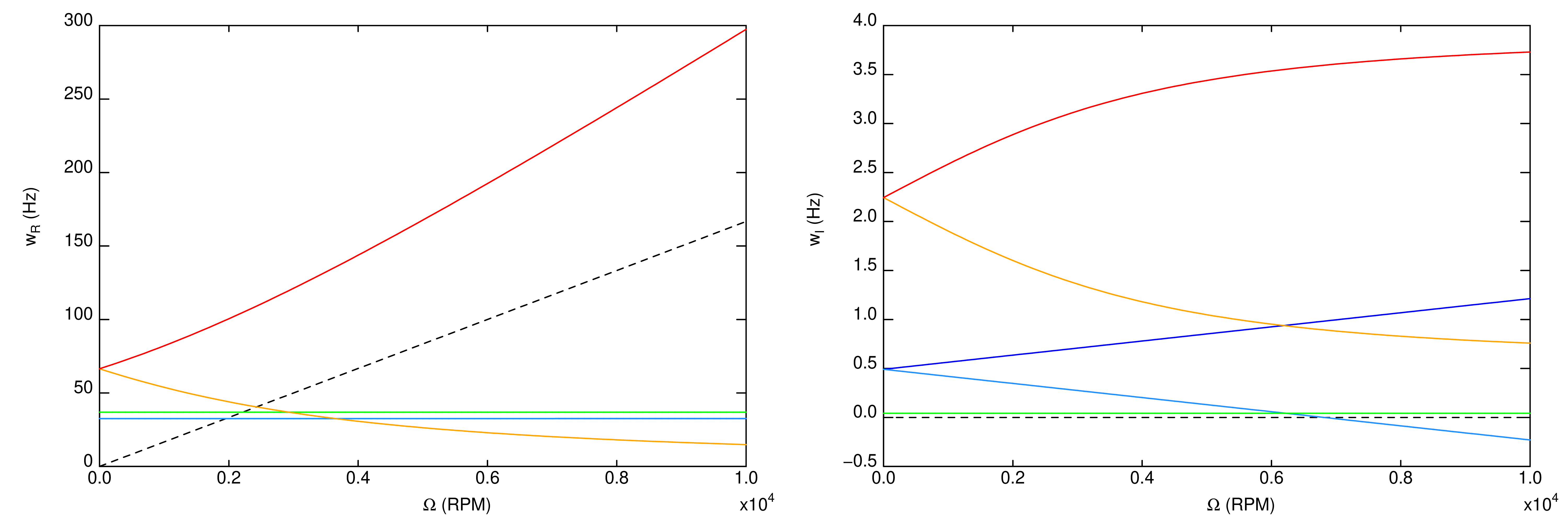
Partie réelles et imaginaire des fréquences des modes complexes
7.1.4. Calcul de la réponse au balourd
On calcule la réponse du rotor à une excitation tournante synchrone avec la vitesse de rotation \(\Omega\).
Extrait du script Cast3M : Calcul de la réponse au balourd
323*******************************************************************************
324* CALCUL DE LA REPONSE A UN BALOURD
325*******************************************************************************
326
327* OMEG2 en RoundPerMinute
328 si (NbModR < 6);
329* PR_RPM2 = prog 0.1E3 'PAS' 0.1E3 10.E3;
330 PR_RPM2 = prog 0.1E3 'PAS' 0.05E3 1.5E-3 'PAS' 0.002E3 2.5E3 'PAS' 0.1E3 10.E3;
331 sinon;
332 PR_RPM2 = prog 0.1E3 'PAS' 0.05E3 1.5E-3 'PAS' 0.002E3 2.5E3 'PAS' 0.1E3 20.E3;
333 finsi;
334
335* on choisit l'unite pour OMEG2 = rad/s
336* G, Krot, Fbal sont definis pour 1 rad/s --> pas de conversion :)
337 UNIT_OMEG2 = mot 'rad/s'; PROMEG2 = (2.*pi/60.) * PR_RPM2 ;
338 cha_x = chai '\W ('UNIT_OMEG2')';
339 NOMEG2 = DIME PROMEG2;
340
341* DESCRIPTION SPATIALE DU BALOURD
342* ici, force tournante autoure de Z, unitaire et appliquée en Z~0.75L
343 pbal = dtot POIN 'PROCH' (0.5 *(p1b PLUS p2));
344 FbalX = FORC 'FX' 1. pbal;
345 FbalY = FORC 'FY' -1. pbal;
346* description frequentielle = le balourd varie en W^2
347* on pose F(W=1rad/s)=1
348 FbalP = (PJBA FbalX TBasR1)
349 ET (EXCO (PJBA FbalY TBasR1) 'FALF' 'IFAL');
350* de sorte que :
351* F(t) = F * cos(wt) - FI * sin(wt)
352* = FX* cos(wt) - FY * sin(wt)
353* = eX* cos(wt) + eY * sin(wt)
354* --> sens de rotation = +eZ
355
356* CREATION DES MATRICES PROJETEE DE TAILLE DOUBLE
357 Mharm = IMPE M1P 'MASSE' ;
358* G est calcule pour 1 rad/s -> on mutliplie par FAC_G
359 Gharm = IMPE G1P 'AMOR' ;
360 Kharm = IMPE K1P 'RAIDEUR' ;
361 Charm = IMPE C1P 'AMOR' ;
362 KRharm= IMPE KROT1P 'RAIDEUR' ;
363
364* REM : il serait possible d'utiliser directement la procedure balourd,
365* mais il semble plus pedagogique de reecrire ici la boucle et le calcul
366
367* CREATION DE NbModR LISTREELS DE TAILLE NOMEG2
368 TqR = TABL;
369 TqI = TABL;
370 REPE BmodR NbModR;
371 TqR . &BmodR = PROG NOMEG2*0.;
372 TqI . &BmodR = PROG NOMEG2*0.;
373 FIN BmodR;
374
375* ON BOUCLE SUR LES FREQUENCES DE ROTATION Omega_j ---------------------
376 REPE BOMEG2 NOMEG2;
377 Omega_j = EXTR PROMEG2 &BOMEG2;
378 MESS 'Calcul de la reponse au balourd pour \W=' Omega_j ' ' UNIT_OMEG2;
379
380* on va resoudre : [ [ K - W^2*M ] -[W*C + W^2*G] ] * ( U) = ( F)
381* [ [W*C + W^2*G] [ K - W^2*M ] ] * (IU) = (IF)
382 Kdyn = ( Kharm ET (Omega_j * KRharm) )
383 ET (Omega_j * (Charm ET (Omega_j * Gharm)) )
384 ET ((Omega_j**2) * Mharm);
385 Fdyn = (Omega_j**2) *FbalP ;
386 Udyn = RESO Kdyn Fdyn;
387
388* extraction des resultats modaux : on stocke dans les listreels finaux
389 REPE BmodR NbModR;
390 ptrep_j = TBasR1 . 'MODES' . &BmodR . 'POINT_REPERE';
391 REMP (TqR . &BmodR) &BOMEG2 (EXTR Udyn 'ALFA' ptrep_j);
392 REMP (TqI . &BmodR) &BOMEG2 (EXTR Udyn 'IALF' ptrep_j);
393 FIN BmodR;
394
395 FIN BOMEG2 ;
396* FIN DE LA BOUCLE SUR LES FREQUENCES DE ROTATION ----------------------
397
398
399* POST-TRAITEMENT GRAPHIQUE
400 colors = @PALETTE NbModR;
401 evqAMP = VIDE 'EVOLUTIO';
402 evqNYQ = VIDE 'EVOLUTIO';
403 REPE BmodR NbModR;
404 coco = EXTR colors &BmodR;
405 leg1 = CHAI 'q_{'&BmodR'}';
406 prqAMP1 = ( ((TqR . &BmodR)**2) + ((TqI . &BmodR)**2) )**0.5;
407 evqAMP = evqAMP
408 et (EVOL coco 'MANU' 'LEGE' leg1 '\W (RPM)' PR_RPM2 '|q|' prqAMP1);
409 evqNYQ = evqNYQ
410 et (EVOL coco 'MANU' 'LEGE' leg1 'q_{R}' (TqR . &BmodR) 'q_{I}' (TqI . &BmodR));
411 FIN BmodR;
412
413si GRAPH;
414 TqAMP = TABL;
415 TqAMP . 2 = MOT 'TIRR';
416 TqAMP . 5 = MOT 'TIRR';
417 TqAMP . 7 = MOT 'TIRR';
418 TqAMP . 9 = MOT 'TIRR';
419 TITR 'Unbalance response : amplitude';
420 DESS evqAMP TqAMP;
421 DESS evqAMP LOGY YBOR 1.E-5 1.E1 TqAMP;
422 TITR 'Unbalance response : Nyquist';
423 DESS evqNYQ 'CARR' LEGE ;
424finsi;
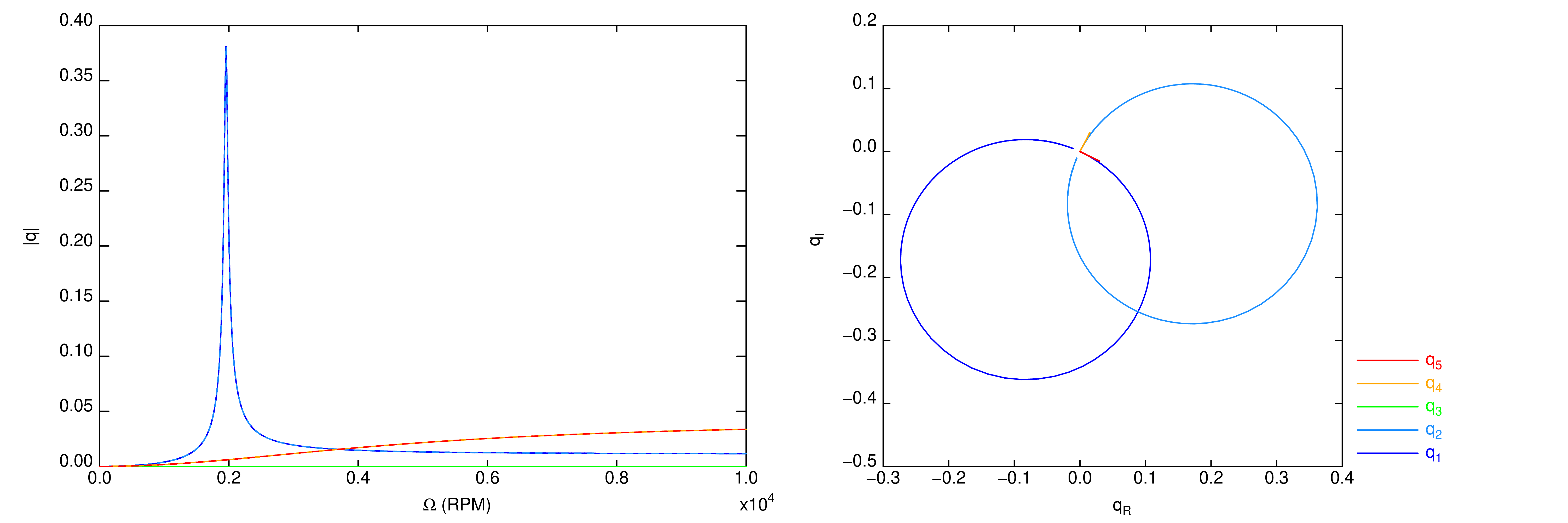
Amplitude et diagramme de Nyquist de la réponse modale à un balourd