2. Rappels sur les éléments finis barre, poutres et poutres à fibre

2.1. Généralités sur les éléments barres et poutres

Plusieurs types d'éléments finis de type poutre sont disponibles dans Cast3M pour l'étude de structures. Ces éléments finis sont basés sur des supports géométriques de segments à deux noeuds (éléments géométrique SEG2).

Les noms d'éléments finis disponibles pour ces supports géométriques sont :

l'élément BARR, modélisant uniquement la traction et la compression.
l'élément POUT, basé sur la théorie des poutres d'Euler-Beroulli, où la section droite reste droite et orthogonale à la fibre moyenne, négligeant la déformation de cisaillement et avec une répartition de courbure linéaire sur l’élément ;
l’élément TIMO, basé sur la théorie des poutres de Timoshenko, où la section droite reste droite mais pas nécessairement orthogonale à la fibre moyenne, avec déformation de cisaillement et avec une répartition de courbure constante sur l’élément.

Ces éléments finis fonctionnent en 3D et en 2D (contraintes planes et déformations planes).

À ces éléments finis s'ajoute la modélisation poutre multifibres. Il s'agit d'un élément TIMO, représentant la fibre moyenne de la poutre, auquel on lie un second modèle de section représentant une échelle plus fine : celle de la section droite. Le modèle de section est basé sur un maillage d'éléments finis massifs classique 2D.

TODO : Récapitulatif des paramètres materiau et géométriques obligatoires en élasticité YOUN, NU, SECT, INRY, INRZ, INRX, et aussi sections réduites

TODO : Tableau synthétique des déformations (allongement, cisaillements, dérivée de torsion, courbures) et contraintes (effort axial, tranchants, moments de flexion, de torsion) généralisées pour les POUT/TIMO avec nom Cast3M des composantes

Dans la suite de cette documentation, nous traiterons de l'élément fini TIMO car plus générique et distinguerons l'élément POUT quand nécessaire.

2.2. Bibliographie

Plus d'informations sur la modélisation multifibres peuvent être trouvées dans les références suivantes (dont une partie de ces rappels sont issus) :

D. Combescure Modélisation des structures de génie civil sous chargement sismique à l’aide de castem 2000. Rapport CEA/DEN/SAC/DM2S/SEMT/EMSI/RT/01-008/A, CEA, 2001

J. Guedes, P. Pegon, and A. V. Pinto A Fibre/Timoshenko Beam Element in Castem 2000. Technical Report I.94.31, Applied Mechanics Unit, Safety Technology Institute, Joint Research Centre, European Commission, 1994

L. Adelaide, B. Richard, C. Cremona Un modèle efficace pour la prédiction du comportement d’éléments de structure en beton armé corrodés : Application aux poutres de la rance GC’2011 L’innovation dans le génie civil, au service de la construction durable, France, 2011

2.3. Éléments finis poutre de Timoshenko

2.3.1. Notations

La figure suivante illustre les notations utilisées dans la suite du document. Il s'agit de fixer les conventions d'écriture des grandeurs mécaniques dans le repère global de l'espace et le repère local de la poutre ainsi que de définir les déformations et contraintes généralisées.

Dans le repère global \((O,\underline{X},\underline{Y},\underline{Z})\) :

\(P\) désigne un point quelconque de la poutre et \((X,Y,Z)\) ses coordonnées ;
\(S\) désigne la section droite de la poutre où se trouve \(P\) ;
\(G\) désigne le centre la section droite \(S\) ;
\(F\) désigne la ligne formée par l'ensemble des points \(G\) de toutes les sections droites de la poutre, cette ligne est appelée fibre moyenne ;
\(U_X, U_Y, U_Z\) désignent les déplacement de \(G\) (composantes UX, UY, UZ du modèle Cast3M) ;
\(R_X, R_Y, R_Z\) désignent les rotations de \(S\) (composantes RX, RY, RZ du modèle Cast3M).

On note \(x\) l'abscisse curviligne du point \(G\) le long de \(F\) et on définit un repère local \((G,\underline{x},\underline{y},\underline{z})\) où \(\underline{x}\) est tangent à la fibre moyenne \(F\) et \(\underline{y}\) et \(\underline{z}\) sont dans le plan de la section droite \(S\).

Dans le repère local \((G,\underline{x},\underline{y},\underline{z})\) :

\(P\) peut être repéré par ses coordonnés \((x,y,z)\), où \(x\) est l'abscisse curviligne de \(G\) et \((y,z)\) les distances de \(P\) à \(G\) dans le plan de \(S\) ;
\(U_x, U_y, U_z\) désignent les déplacements de \(G\) ;
\(R_x, R_y, R_z\) désignent les rotations de \(S\).

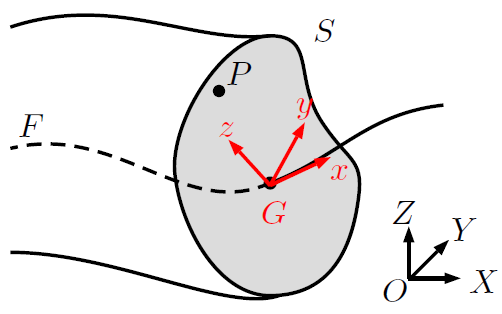
../_images/schema_poutre_1.png — Schéma de la poutre avec sa fibre moyenne \(F\) et une section droite \(S\). Le repère local au centre \(G\) de la section droite est en rouge.

2.3.2. Déplacements

Les hypothèses cinématiques de la théorie de Timoshenko permettent d'exprimer la cinématique de tout point \(P\) de la poutre en fonction des déplacements de \(G\), des rotations de \(S\) et des coordonnées de \(P\).

Ainsi, le déplacement \(\underline{u}\) du point \(P\) s'écrit:

\[\begin{split}\underline{u}= \left[ \begin{array}{c} u_x \\ u_y \\ u_z \end{array} \right]= \left[ \begin{array}{l} U_x + zR_y - yR_z \\ U_y - zR_x \\ U_z + yR_x \end{array} \right]\end{split}\]

2.3.3. Déformations

Sous l'hypothèse des petites déformations, les composantes du tenseur des déformations au point \(P\) s'écrivent :

(1)\[\begin{split}\varepsilon_{xx} & = \frac{\partial u_x}{\partial x}\phantom{+\frac{\partial u_x}{\partial x}} & = \frac{dU_x}{dx}+z\frac{dR_y}{dx}-y\frac{dR_z}{dx} \\ \gamma_{xy} & = \frac{\partial u_x}{\partial y}+\frac{\partial u_y}{\partial x} & = \frac{dU_y}{dx}-R_z-z\frac{dR_x}{dx} \\ \gamma_{xz} & = \frac{\partial u_x}{\partial z}+\frac{\partial u_z}{\partial x} & = \frac{dU_z}{dx}+R_y+y\frac{dR_x}{dx}\end{split}\]

où :

\(\varepsilon_{xx}\) est la déformation axiale au point \(P\) ;
\(\gamma_{xy},\gamma_{xz}\) sont les cisaillements au point \(P\).

On peut réécrire les déformations au point \(P\) en faisant apparaitre celles du point \(G\), centre de la fibre moyenne :

(2)\[\begin{split}\varepsilon_{xx} & = E_x+z\Phi_y-y\Phi_z \\ \gamma_{xy} & = \Gamma_y-z\Phi_x \\ \gamma_{xz} & = \Gamma_z+y\Phi_x\end{split}\]

Les déformations au centre de la section \(G\) sont appelées les déformations généralisées :

(3)\[\begin{split}E_x = \frac{dU_x}{dx} & \qquad & \Phi_x = \frac{dR_x}{dx} \\ \Gamma_y = \frac{dU_y}{dx} & \qquad & \Phi_y = \frac{dR_y}{dx} \\ \Gamma_z = \frac{dU_z}{dx} & \qquad & \Phi_z = \frac{dR_z}{dx}\end{split}\]

2.3.4. Contraintes

La théorie des poutres définit l'effort axial \(F_x\) et les moments de flexion \(M_y,M_z\) en intégrant la contrainte axiale \(\sigma_{xx}\) correspondante à la déformation axiale \(\varepsilon_{xx}\).

(4)\[\begin{split}F_x & = \int_{S}\sigma_{xx}dS \\ M_y & = \int_{S}z\sigma_{xx}dS \\ M_z & = -\int_{S}y\sigma_{xx}dS\end{split}\]

De même, on définit les efforts tranchants \(F_y, F_z\) et le moment de torsion \(M_x\) en intégrant les contraintes tangentielles \(\sigma_{xy}, \sigma_{xz}\) déduites des cisaillements \(\gamma_{xy}, \gamma_{xz}\).

(5)\[\begin{split}F_y & = \int_{S}\sigma_{xy}dS \\ F_z & = \int_{S}\sigma_{xz}dS \\ M_x & = \int_{S}(y\sigma_{xz}-z\sigma_{xy})dS\end{split}\]

Les forces \(F_x, F_y, F_z\) et les moments \(M_x, M_y, M_z\) sont appelées les contraintes généralisées.

2.3.5. Remarques

Loi de comportement

Pour un élément poutre TIMO ou POUT, l'écriture de la loi de comportement locale consiste à écrire une relation entre les déformations généralisées \(\left(E_x, \Gamma_y, \Gamma_z, \Phi_x, \Phi_y, \Phi_z\right)\) et les contraintes généralisées \(\left(F_x, F_y, F_z, M_x, M_y, M_z\right)\).

Cette écriture est donc très différente des lois de comportement habituelles de la mécanique des milieux continus, que l'on retrouve dans les éléments finis massifs (où l'on écrit une relation entre les déformations et contraintes locales). De plus, dans les éléments finis de poutre, la loi de comportement est appliquée seulement aux pointx de Gauss de la fibre moyenne de la poutre, ce qui ne permet pas de capter l'hétérogénéité du comportement à travers la section.

Intégration

L'élément TIMO est sous intégré pour éviter les problèmes de blocage en cisaillement (shear locking). Les fonctions de forme sont donc :

de degré 1 pour les rotations, les déplacements transverses et axial ;
constante pour les courbures, les déformations de cisaillement et axiale.

L'élément possède un unique point de Gauss situé au centre de l'élément.

Tableau synthétique des composantes des champs mécaniques

Déplacements/Rotations (inconnues primales)
Notation	Description	Composante dans Cast3M	Support	Exprimé dans le repère
\(U_X\)	déplacement de \(G\) selon \(X\)	UX	Nœuds CHPOINT	Global \((O,\underline{X},\underline{Y},\underline{Z})\)
\(U_Y\)	déplacement de \(G\) selon \(Y\)	UY	Nœuds CHPOINT	Global \((O,\underline{X},\underline{Y},\underline{Z})\)
\(U_Z\)	déplacement de \(G\) selon \(Z\)	UZ	Nœuds CHPOINT	Global \((O,\underline{X},\underline{Y},\underline{Z})\)
\(R_X\)	rotation de \(S\) autour de \(X\)	RX	Nœuds CHPOINT	Global \((O,\underline{X},\underline{Y},\underline{Z})\)
\(R_Y\)	rotation de \(S\) autour de \(Y\)	RY	Nœuds CHPOINT	Global \((O,\underline{X},\underline{Y},\underline{Z})\)
\(R_Z\)	rotation de \(S\) autour de \(Z\)	RZ	Nœuds CHPOINT	Global \((O,\underline{X},\underline{Y},\underline{Z})\)

Forces/Moments (inconnues duales)
Notation	Description	Composante dans Cast3M	Support	Exprimé dans le repère
\(F_X\)	force en \(G\) selon \(X\)	FX	Nœuds CHPOINT	Global \((O,\underline{X},\underline{Y},\underline{Z})\)
\(F_Y\)	force en \(G\) selon \(Y\)	FY	Nœuds CHPOINT	Global \((O,\underline{X},\underline{Y},\underline{Z})\)
\(F_Z\)	force en \(G\) selon \(Z\)	FZ	Nœuds CHPOINT	Global \((O,\underline{X},\underline{Y},\underline{Z})\)
\(M_X\)	moment en \(G\) autour de \(X\)	MX	Nœuds CHPOINT	Global \((O,\underline{X},\underline{Y},\underline{Z})\)
\(M_Y\)	moment en \(G\) autour de \(Y\)	MY	Nœuds CHPOINT	Global \((O,\underline{X},\underline{Y},\underline{Z})\)
\(M_Z\)	moment en \(G\) autour de \(Z\)	MZ	Nœuds CHPOINT	Global \((O,\underline{X},\underline{Y},\underline{Z})\)

Déformations généralisées
Notation	Description	Composante dans Cast3M	Support	Exprimé dans le repère
\(E_x = \frac{dU_x}{dx}\)	déformation/élongation axiale moyenne	EPS	Point de Gauss MCHAML	Local \((G,\underline{x},\underline{y},\underline{z})\)
\(\Gamma_y = \frac{dU_y}{dx}\)	déformation de cisaillement \(xy\) moyenne	GXY	Point de Gauss MCHAML	Local \((G,\underline{x},\underline{y},\underline{z})\)
\(\Gamma_z = \frac{dU_z}{dx}\)	déformation de cisaillement \(xz\) moyenne	GXZ	Point de Gauss MCHAML	Local \((G,\underline{x},\underline{y},\underline{z})\)
\(\Phi_x = \frac{dR_x}{dx}\)	dérivé de la rotation de torsion	CX	Point de Gauss MCHAML	Local \((G,\underline{x},\underline{y},\underline{z})\)
\(\Phi_y = \frac{dR_y}{dx}\)	courbure autour de \(y\)	CY	Point de Gauss MCHAML	Local \((G,\underline{x},\underline{y},\underline{z})\)
\(\Phi_z = \frac{dR_z}{dx}\)	courbure autour de \(z\)	CZ	Point de Gauss MCHAML	Local \((G,\underline{x},\underline{y},\underline{z})\)

Contraintes généralisées
Notation	Description	Composante dans Cast3M	Support	Exprimé dans le repère
\(F_x = \int_{S}\sigma_{xx}dS\)	effort axial selon \(x\)	EFFX	Point de Gauss MCHAML	Local \((G,\underline{x},\underline{y},\underline{z})\)
\(F_y = \int_{S}\sigma_{xy}dS\)	effort tranchant selon \(y\)	EFFY	Point de Gauss MCHAML	Local \((G,\underline{x},\underline{y},\underline{z})\)
\(F_z = \int_{S}\sigma_{xz}dS\)	effort tranchant selon \(z\)	EFFZ	Point de Gauss MCHAML	Local \((G,\underline{x},\underline{y},\underline{z})\)
\(M_x = \int_{S}(y\sigma_{xz}-z\sigma_{xy})dS\)	moment de torsion autour de \(x\)	MOMX	Point de Gauss MCHAML	Local \((G,\underline{x},\underline{y},\underline{z})\)
\(M_y = \int_{S}z\sigma_{xx}dS\)	moment fléchissant autour de \(y\)	MOMY	Point de Gauss MCHAML	Local \((G,\underline{x},\underline{y},\underline{z})\)
\(M_z = -\int_{S}y\sigma_{xx}dS\)	moment fléchissant autour de \(z\)	MOMZ	Point de Gauss MCHAML	Local \((G,\underline{x},\underline{y},\underline{z})\)

2.4. Éléments finis poutre multifibres

Dans Cast3M, les éléments finis de poutre multifibres sont basés sur des éléments poutre de Timoshenko mais présentent deux niveaux de modélisation :

le niveau "poutre" repose sur un modèle linéique de la fibre moyenne, constitué d'éléments finis TIMO, présentés dans le paragraphe précédent ;
le niveau "section" repose sur un modèle surfacique de la section droite, constitué d'éléments finis massifs classiques 2D (triangles et/ou quadrangles linéaires).

Les liaisons entre les deux niveaux de modélisation peuvent être résumées sur la figure ci-dessous.

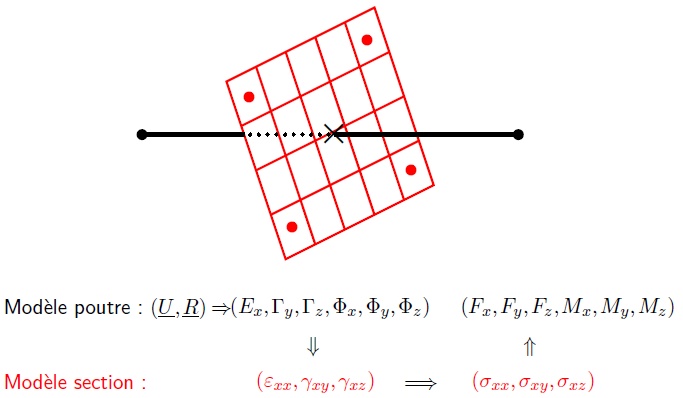
../_images/schema_poutre_2.png — Schéma du modèle de poutre multifibres. Pour un élément fini poutre **TIMO** (noir) est associé un modèle de section (rouge).

À partir des déplacements et rotations aux noeuds du modèle poutre \((\underline{U},\underline{R})\), on peut déduire les déformations généralisées \((E_x,\Gamma_y,\Gamma_z,\Phi_x,\Phi_y,\Phi_z)\) au point de Gauss de la poutre (3). Ces déformations traduisent la déformation moyenne de la section.
On peut localiser, en chaque point de Gauss du modèle section, les déformations \((\varepsilon_{xx},\gamma_{xy},\gamma_{xz})\) en appliquant les équations (2).
La loi de comportement est appliquée en chaque point de Gauss du modèle section ce qui donne les contraintes \((\sigma_{xx},\sigma_{xy},\sigma_{xz})\).
On remonte, par homogénéisation, aux contraintes généralisées du modèle poutre \((F_x,F_y,F_z,M_x,M_y,M_z)\) en appliquant les équations (4) et (5).

Les lois de comportement locales du modèle de section, sont similaires à celles de la mécanique des milieux continus car elles portent sur de "vraies" déformations et contraintes, et non pas entre les contraintes et déformations généralisées du modèle poutre. De plus, la finesse du maillage de la section permet de représenter les hétérogéités de comportement dans la section.

Ce type d'élément a notamment été développé pour des applications en génie civil où, par exemple, une structure en béton armé peut être modélisée de manière simplifiée à l'échelle de la structure (modèle linéique et homogène de poutre) tout en prenant en compte la présences des ferraillages dans la section (modèle hétérogène de section) et notamment la différence de comportement entre le béton et les armatures en acier.

Cependant, la cinématique des poutres de Timoshenko contraint l'écriture de la loi de comportement locale dans la section à une forme unidimensionnelle associant les contraintes axiale \(\sigma_{xx}\) et tangentielles \(\sigma_{xy}, \sigma_{xz}\) respectivement aux déformations axiale \(\varepsilon_{xx}\) et de cisaillement \(\gamma_{xy},\gamma_{xz}\). Dans Cast3M, les lois de comportement locales des poutres multifibres sont écrites en supposant que la non linéarité n'est portée que sur la composante axiale \(x\).

TODO : exemple d'utilisation modèle de SECTION sur les éléments TIMO et de leurs paramètres obligatoires MODS, MATS, VECT

TODO : exemple d'utilisation modèles non linéaires sur les éléments QUAS/TRIS/SEGS/POJS

TODO : récapitulatif paramètres materiau/géométriques obligatoires en élasticité YOUN, NU, ALPY, ALPZ, SECT (pour les POJS et BARR), LARG (pour les SEGS)