Test name
ther7or
Calculation type
THERMAL STEADY STATE
D ORTHOTROPIC
Finite element type
COQ8 COQ6
Topic
Test of the boundary conditions of temperature with orthotropic elements.
Three different configurations are tested on a shell :
Goal
Find the field of temperatures in the shell for each configuration and compare
it with the case of isotropic elements.
Reference CASTEM
Dowlatyari (03/91).
Version
97' customer version
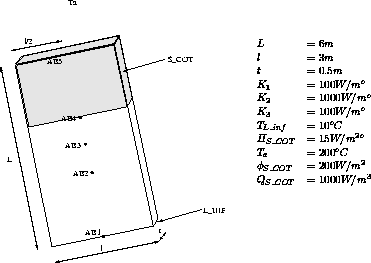
Model description
Test ther7or Results
CASTEM figures
* Test Ther7or.dgibi: Jeux de données *
* ----------------------------------- *
* *
SAUT PAGE ;
*-----------------------------------------------------*
* TEST THER7OR *
* *
* TEST DES CL DE TEMPERATURE POUR COQ8 ET COQ6 *
* ORTHOTROPE *
* -------------------------------------------- *
* *
* TEMPERATURE IMPOSEE + CONVECTION *
* + FLUX *
* + SOURCE *
* *
* Ce test permet de vérifier le bon fonctionnement *
* des divers opérateurs thermiques de CASTEM2000 en *
* ORTHOTROPIE *
* *
* UNE PLAQUE RECTANGULAIRE CONSTITUEE D'éléments COQ8 *
* et coq6 est soumise à une température imposée à une *
* de ses extrémités et sucessivement à une condition *
* de convection forcée, à une condition de flux impo- *
* -sé et à une condition de source volumique imposée. *
* *
* *
* Il s'agit du meme probleme que pour le test ther71. *
* Mais on utilise un materiau orthotrope au lieu d'un *
* materiau isotrope avec la meme conductivite suivant *
* l'axe A1A7. Or le gradient de temperature etant *
* parallele a cet axe, on doit obtenir un resultat *
* identique. *
* On compare donc les resultats obtenus a ceux du *
* test ther71 pour les elements coques. *
* *
* Test elabore par Mr Dowlatyari 03/91. *
* Test modifie pour evolution 21/05/92. *
* *
*-----------------------------------------------------*
opti echo 1;
opti trac bens;
graph = 'N';
SAUT PAGE ;
*
TITRE 'C.L. DE TEMPERATURE - ELEMENTS COQ8 , COQ6 ' ;
OPTION DIME 3 ELEM QUA8 ;
TEMPS ;
*
*CREATION DE LA GEOMETRIE: POINTS SUPPORTS DES ELEMENTS
*
A1 = 0. 0. 0. ; B1 = 0. 3.0 0. ;AB1 =0. 1.5 0. ;
A2= 0. 0. 1. ; B2 = 0. 3. 1. ; AB2 = 0. 1.5 2. ;
A3 = 0. 0. 2. ; B3 = 0. 3. 2. ; AB4 = 0. 1.5 4. ;
A4 = 0. 0. 3. ; B4 = 0. 3. 3. ; AB5 = 0. 1.5 6. ;
A5 = 0. 0. 4. ;B5 = 0. 3. 4. ; AB3= 0. 1.5 3. ;
A6 = 0. 0. 5. ;B6 = 0. 3. 5. ;
A7 = 0. 0. 6. ;B7 = 0. 3. 6. ;
M=0. 0. 0. ;N=2. 0. 0. ;
*
ANG=20.0 ;
A1=A1 TOUR ANG M N ;A2=A2 TOUR ANG M N ;
A3=A3 TOUR ANG M N ;A4=A4 TOUR ANG M N ;
A5=A5 TOUR ANG M N ;A6=A6 TOUR ANG M N ;
A7=A7 TOUR ANG M N ;B1=B1 TOUR ANG M N ;
B2=B2 TOUR ANG M N ;B3=B3 TOUR ANG M N ;
B4=B4 TOUR ANG M N ;B5=B5 TOUR ANG M N ;
B6=B6 TOUR ANG M N ;B7=B7 TOUR ANG M N ;
AB1=AB1 TOUR ANG M N ;AB2=AB2 TOUR ANG M N ;
AB3=AB3 TOUR ANG M N ;AB4=AB4 TOUR ANG M N ;
AB5=AB5 TOUR ANG M N ;
*------- CREATION DES QUADRANGLES ET TRIANGLES -------
*
QH01 = MANU QUA8 A1 AB1 B1 B2 B3 AB2 A3 A2 ;
QH02 = MANU TRI6 A3 AB2 B3 B4 B5 AB3 ;
QH03 = MANU TRI6 A3 AB3 B5 AB4 A5 A4 ;
QH04 = MANU QUA8 A5 AB4 B5 B6 B7 AB5 A7 A6 ;
*
*
QTOT = QH01 ET QH02 ET QH03 ET QH04 ;
si ( NEG GRAPH 'N' );
OEIL = 100. 100. 100. ;
TRACE OEIL QTOT;
finsi;
QSOUR = QH04 ;
*
*
L_INF = MANU SEG3 A1 AB1 B1 ;
*
S_COT = QH04;
*
* ATTENTION : il faut réorienter les éléments
* (OPERATEUR ORIENT) si on n'est pas sur que tous les
* éléments sont orientés d'une façon cohérante
*
*----------- DONNEES DU PROBLEME DE THERMIQUE --------
*
*-------------- MODELISATION ------------------------
*
MOD1 = MODL QTOT THERMIQUE ORTHOTROPE COQ8 COQ6 ;
MOD2 = MODL S_COT CONVECTION SUPERIEURE COQ8 COQ6 ;
*
*------ DONNEES DES CARACTERISTIQUES DU MATERIAU ------
*
MAT1 = MATR MOD1 'DIRECTION' A2 'PARALLELE'
'K1' 100. 'K2' 1000. 'K3' 100. EPAI 0.5 ;
MAT2 = MATR MOD2 'H' 15. ;
*
*------- CREATION DES MATRICES DE CONDUCTIVITE --------
*
*OPTION DONN 5 ;
CND1 = CONDUCTIVITE MOD1 MAT1 ;
CND2 = CONDUCTIVITE MOD2 MAT2 ;
*
*-------- TEMPERATURES IMPOSEES: BLOQUE + DEPI --------
*
BB1 = BLOQUE L_INF 'TINF' ;
EE1 = DEPI BB1 10. ;
BB2 = BLOQUE L_INF 'TSUP' ;
EE2 = DEPI BB2 10. ;
BB3 = BLOQUE L_INF 'T ' ;
EE3 = DEPI BB3 10. ;
BB = BB1 ET BB2 ET BB3 ;
EE = EE1 ET EE2 ET EE3 ;
*
*--- FLUX EQUIVALENTS A LA CONDITION DE CONVECTION ----
*
CNV1 = CONVECTION MOD2 MAT2 'T' 200.;
*
*--------------- FLUX IMPOSE --------------------------
*
FLU1 = FLUX MOD1 200. S_COT SUPE ;
*
*--------------- SOURCE DE CHALEUR --------------------
*
list qsour;
S1 = SOURCE MOD1 MAT1 1000. QSOUR ;
list s1;
*
*-------- ASSEMBLAGE DES TERMES DE CONDUCTIVITE -------
*
CCC1 = CND1 ET CND2 ET BB ;CCC2 = CND1 ET BB ;
*
*------ ASSEMBLAGE DES TERMES DE FLUX EQUIVALENTS -----
*
FFF1 = EE ET CNV1 ;FFF2 = EE ET FLU1 ;FFF3 = EE ET S1 ;
*FFF1 = EE ET CNV1 ;FFF2 = EE ET FLU1 ;
*
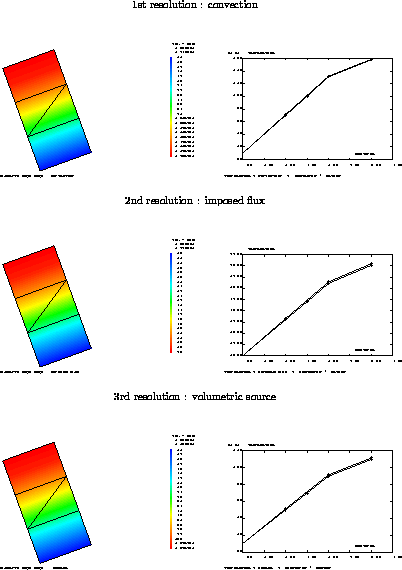
*----------- 1ERE RESOLUTION : CONVECTION -------------
*
*OPTION DONN 5 ;
CHTER1 = RESOUDRE CCC1 FFF1 ;
*
*---------------- 2EME RESOLUTION : FLUX --------------
*
CHTER2 = RESOUDRE CCC2 FFF2 ;
*
*---------------- 3EME RESOLUTION: SOURCE -------------
*
CHTER3 = RESOUDRE CCC2 FFF3 ;
*
*----- POST-TRAITEMENT: TRACE DES CHAMPS RESULTATS ----
*------ ET EXTRACTION DES VALEURS CARACTERISTIQUES ----
*
*LISTE CHTER1 ;
*LISTE CHTER2 ;
*LISTE CHTER3 ;
*
OEIL= 1000. 0. 0. ;
*
SI (NEG GRAPH 'N');
TITRE 'ELEMENTS COQ6,COQ8 : CONVECTION' ;
CHTER1I = 'EXCO' CHTER1 'TINF' 'NOID' 'TINF' ;
TRACER OEIL QTOT CHTER1I ;
TITRE 'ELEMENTS COQ6,COQ8 : FLUX IMPOSE' ;
CHTER2I = 'EXCO' CHTER2 'TINF' 'NOID' 'TINF' ;
TRACER OEIL QTOT CHTER2I ;
TITRE 'ELEMENTS COQ6,COQ8 : SOURCE' ;
CHTER3I = 'EXCO' CHTER3 'TINF' 'NOID' 'TINF' ;
TRACER OEIL QTOT CHTER3I ;
FINSI;
T1AB1 = EXTR CHTER1 TSUP AB1 ;
T1AB2=EXTR CHTER1 TSUP AB2 ;
T1AB3 = EXTR CHTER1 TSUP AB3 ;
T1AB4=EXTR CHTER1 TSUP AB4 ;
T1AB5 = EXTR CHTER1 TSUP AB5 ;
T2AB1= EXTR CHTER2 TSUP AB1 ;
T2AB2=EXTR CHTER2 TSUP AB2 ;
T2AB3 = EXTR CHTER2 TSUP AB3 ;
T2AB4=EXTR CHTER2 TSUP AB4 ;
T2AB5 = EXTR CHTER2 TSUP AB5 ;
T3AB1 = EXTR CHTER3 TSUP AB1 ;
T3AB2=EXTR CHTER3 TSUP AB2 ;
T3AB3 = EXTR CHTER3 TSUP AB3 ;
T3AB4=EXTR CHTER3 TSUP AB4 ;
T3AB5 = EXTR CHTER3 TSUP AB5 ;
*
SI ( NEG GRAPH 'N') ;
DIST = PROG 0. 2. 4. 6. ;
DIST1 = PROG 0. 2. 3. 4. 6. ;
TEMPR1=PROG 10. 71.44 132.03 158.86 ;
TEMPC1= PROG T1AB1 T1AB2 T1AB3 T1AB4 T1AB5 ;
EV1R = EVOL MANU 'DISTANCE' DIST 'TEMPERATURE' TEMPR1 ;
EV1C = EVOL MANU 'DISTANCE' DIST1 'TEMPERATURE' TEMPC1;
TAB = 'TABLE' ;
TAB.1 = 'MARQ PLUS' ;
TAB.2 = 'MARQ ETOI' ;
TITRE 'COQ6 ET COQ8 ;TEMPERATURE + CONVECTION ;+ :
MASSIF,* : COQUE' ;
DESSIN TAB (EV1R ET EV1C ) ;
TEMPR2=PROG 10. 26.58 42.878 50.984 ;
TEMPC2= PROG T2AB1 T2AB2 T2AB3 T2AB4 T2AB5 ;
EV2R = EVOL MANU 'DISTANCE' DIST 'TEMPERATURE' TEMPR2 ;
EV2C = EVOL MANU 'DISTANCE' DIST1 'TEMPERATURE' TEMPC2;
TITRE 'COQ6 ET COQ8;TEMPERATURE + FLUX IMPOSE ;+ :
MASSIF,* : COQUE';
DESSIN TAB (EV2R ET EV2C ) ;
TEMPR3=PROG 10. 51.43 91.75 111.75 ;
TEMPC3= PROG T3AB1 T3AB2 T3AB3 T3AB4 T3AB5 ;
EV3R = EVOL MANU 'DISTANCE' DIST 'TEMPERATURE' TEMPR3 ;
EV3C = EVOL MANU 'DISTANCE' DIST1 'TEMPERATURE' TEMPC3;
TITRE 'COQ6 ET COQ8 ;TEMPERATURE + SOURCE ;+
MASSIF,* : COQUE ';
DESSIN TAB (EV3R ET EV3C ) ;
TEMPS ;
FINSI;
T1Aq = 10.; T1Bq = 71.44; t1Cq = 132.03; T1DQ = 158.86;
T2Aq = 10.; T2Bq = 26.58; t2Cq = 42.878; T2DQ = 50.984;
T3AQ = 10.; T3BQ = 58.38; T3CQ = 105.34 ; T3DQ = 123.33;
*******************************************************
************** TEST DE FONCTIONNEMENT ****************
*******************************************************
mess t1ab1 T1Aq T1AB2 T1Bq;
mess T1AB4 T1Cq T1AB5 T1Dq;
mess T2AB1 T2Aq T2AB2 T2Bq;
mess T2AB4 T2Cq T2AB5 T2Dq;
mess T3AB1 T3Aq T3AB2 T3Bq;
mess T3AB4 T3Cq T3AB5 T3Dq;
ERCA= ABS (( T1AB1-T1Aq)/T1AB1);
ERCB= ABS (( T1AB2-T1Bq)/T1AB2);
ERCC= ABS (( T1AB4-T1Cq)/T1AB4);
ERCD= ABS (( T1AB5-T1Dq)/T1AB5);
ERFA= ABS (( T2AB1-T2Aq)/T2AB1);
ERFB= ABS (( T2AB2-T2Bq)/T2AB2);
ERFC= ABS (( T2AB4-T2Cq)/T2AB4);
ERFD= ABS (( T2AB5-T2Dq)/T2AB5);
ERSA= ABS (( T3AB1-T3Aq)/T3AB1);
ERSB= ABS (( T3AB2-T3Bq)/T3AB2);
ERSC= ABS (( T3AB4-T3Cq)/T3AB4);
ERSD= ABS (( T3AB5-T3Dq)/T3AB5);
ERTOT = PROG ERCA ERCB ERCC ERCD ERFA ERFB ERFC ERFD
ERSA ERSB ERSC ERSD;
ermax = maxi ertot;
temps;
SI ( ERMAX <EG 0.05 );
ERRE 0;
SINON;
ERRE 5;
FINSI;
fin;
Test ther7or Comments
MOD1 = MODEL QTOT THERMIQUE ORTHOTROPE COQ8 COQ6 ;
MAT1 = MATER MOD1 'DIRECTION' A2 'PARALLELE'
'K1' 100. 'K2' 1000. 'K3' 100. EPAI 0.5 ;
The thermal model (MOD1) is defined with the formulation named THERRMIQUE ORTHOTROPE. This model is described by the geometry QTOT, the conductivity of the model is defined with the operator MATER : K1, K2 and K3 are the thermal conductivities and the thickness is equal to 0.5 ; the first orthotropic direction is parallel to the vector defined by A2.
MOD2 = MODEL S_COT CONVECTION SUPERIEURE COQ8 COQ6 ;
MAT2 = MATER MOD2 'H' 15. ;
The model MOD2 defines a convection formulation. The keyword SUPERIEURE indicates that the convection is located on the upper side of the shell.
BB1 = BLOQUE L_INF 'TINF' ;
BB2 = BLOQUE L_INF 'TSUP' ;
BB3 = BLOQUE L_INF 'T ' ;
The shells have 3 degrees of freedom : the inside temperature T, the upper temperature TSUP and the lower temperature TINF.