Test name
ther-perm
Calculation type
THERMAL STEADY STATE
D NON LINEAR
Finite element type
QUA4
Topic
Use of the procedure THERMIC in a non linear steady state.
An endless shell is submitted to a volumetric source of heat and to an imposed temperature on one side. The conductivity is a linear function of the temperature.
Goal
Find the field of temperatures in the shell and compare
it with the analytical solution.
Reference
Version
97' customer version
Model description

Test ther-perm Results
CASTEM figures
* Test Ther-perm.dgibi: Jeux de données *
* ------------------------------------- *
* *
*******************************************************
* *
* Calcul d'une plaque infinie (de largeur 2L) avec *
* une source volumique et température imposéé sur *
* les bords. Conductivité dépend linéairement de la *
* température. *
* *
* Modélisation plane. *
* *
* Auteur : Michel Bulik *
* *
* Date : Décembre 1996 *
* *
* Références : *
* ------------ *
* [1] Klaus-Jürgen Bathe & Mohammad R. Khoshgoftaar,*
* Finite element formulation and solution of *
* non-linear heat transfer, Nuclear Engineering *
* and Design, v. 51 (1979), pp. 389-401 *
* *
* [2] J. Joly, Cas tests non linéaires de validation*
* pour DELFINE, Note technique EMT.SMTS.TTMF *
* 84/29 *
* *
* [3] V. Arpaci, Conduction Heat Transfer, Adison- *
* Wesley, 1966, pp. 130-132 *
* *
*******************************************************
* *
* Les résultats du calcul sont comparés avec la *
* solution analytique (voir [3]). *
* *
*******************************************************
*** Options ...
opti dime 2 elem seg2 echo 1 ;
*** Paramètres ...
L = 5.e-3 ;
ep = L / 10 ;
K0 = 2. ;
beta = 0.025 ;
T0 = 100. ;
q = 10000000. ;
graph = faux ;
*** Points ...
dens ep ;
p1 = 0 0 ;
p2 = 0 ep ;
vechoriz = L 0 ;
*** Lignes ...
li1 = p1 d 1 p2 ;
*** Surface ...
opti elem qua4 ;
su1 = li1 tran vechoriz dini (L/100.) dfin (L/10.);
li2 = cote 3 su1 ;
li3 = cote 2 su1 ;
si(graph) ;
titr 'Le maillage de la plaque' ;
trac su1 ;
finsi ;
*** Modèles ...
mocnd = mode su1 thermique ;
dt1 = -100. ;
T1 = T0 + dt1 ;
K1 = K0 * (beta*dt1 + 1) ;
dt2 = 1000. ;
T2 = T0 + dt2 ;
K2 = K0 * (beta*dt2 + 1) ;
titr 'K(T)' ;
evk = evol manu 'T' (prog T1 T2) 'K' (prog K1 K2) ;
si(graph) ;
dess evk ;
finsi ;
macnd = mate mocnd 'K' evk ;
*** Température imposée ...
blt = bloq T li2 ;
ti1 = depi blt T0 ;
*** Source volumique ...
fl1 = sour mocnd su1 q ;
*** Préparation de table pour THERMIC ...
tabth = table THERMIQUE ;
tabth . 'BLOCAGE' = blt ;
tabth . 'IMPOSE' = ti1 ;
tabth . 'FLUX' = fl1 ;
tabth . 'INSTANT(0)' = manu chpo su1 1 T T0
nature diffus ;
tabth . 'TABCOND' = table ;
tabth . 'TABCOND' . mocnd = evk ;
tabth . 'NIVEAU' = 1 ;
*** Lancement du calcul ...
thermic tabth NONLINEAIRE ;
*** Post-traitement ...
tresu = tabth . TEMPERATURE ;
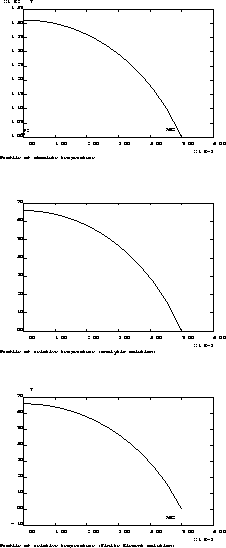
titr 'Profil de temperature absolue' ;
evt = evol chpo tresu T li3 ;
si(graph) ;
dess evt ;
finsi ;
titr
'Profil de temperature relative (solution analytique)';
chx = coor 1 li3 ;
evx = evol chpo chx SCAL li3 ;
lrx = extr evx ABSC ;
lr1 = prog (dime lrx) * 1. ;
ev1 = evol manu lrx lr1 ;
* toto1 = ev1 - ((evx / L)*(evx / L)) ;
* toto1 = ev1 - (extr ((evx / L)*(evx / L)) cour 1) ;
ev1x = extr (evx / L) cour 1;
toto1 = ev1 - (ev1x * ev1x) ;
toto2 = (toto1 * (L*L*q*beta/K0)) + ev1 ;
kkabsc = extr toto2 ABSC ;
kkordo = extr toto2 ORDO ;
toto3 = evol manu kkabsc (kkordo ** 0.5) ;
toto4 = toto3 - ev1 ;
toto5 = (toto4 * (2*K0/(beta*q*L*L))) coul VERT ;
si(graph) ;
dess toto5 ;
finsi ;
titr
'Profil de temperature relative (solution EF)' ;
evtrel = ((evt - (T0 * ev1)) * (2*K0/(q*L*L)))
coul ROUG ;
si(graph) ;
dess (evtrel et toto5) ;
finsi ;
*** Test ...
ladiff = abs (extr (evtrel - toto5) ORDO) ;
valtst = maxi ladiff ;
si(valtst > 1.e-5) ;
erre 5 ;
finsi ;
*** Bye ...
fin ;
Test ther-perm Comments
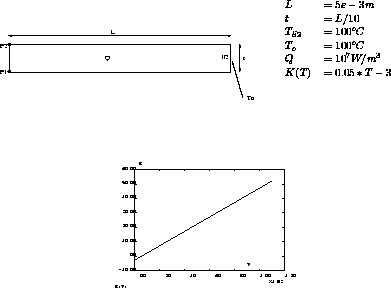
evk = evol manu 'T' (prog T1 T2) 'K' (prog K1 K2) ;
dess evk ;
macnd = mate mocnd 'K' evk ;
The conductivity is a function of the temperature and is defined in the evolution (evk). The declaration of the conductivity is done with the operator mate and the values are given in the shape of the evolution object (evk).
tabth = table THERMIQUE ;
tabth . 'BLOCAGE' = blt ;
tabth . 'IMPOSE' = ti1 ;
tabth . 'FLUX' = fl1 ;
tabth . 'INSTANT(0)' = manu chpo su1 1 T T0 nature diffus ;
tabth . 'TABCOND' = table ;
tabth . 'TABCOND' . mocnd = evk ;
tabth . 'NIVEAU' = 1 ;
thermic tabth NONLINEAIRE ;
The procedure THERMIC enables to deal with non linear permanent conditions. It requires some input data which are given in a table of subtype THERMIQUE. The results of the procedure is a field of temperature which is contained in the same table.
The table tabth has different indexes :
- 'BLOCAGE' : contains the restraint matrix (RIGIDITE type)
- 'IMPOSE' : contains the imposed values (CHPOINT type)
- 'FLUX' : contains the equivalent flow (CHPOINT type)
- 'INSTANT(0)' : contains the initial temperature field (CHPOINT type)
- 'TABCOND' : contains the tables of conductivities indexed by the model object of the different subspaces (here tabth . 'TABCOND' . mocnd contains the evolution of the conductivity evk)
- 'NIVEAU' : indicates the level of message.
tresu = tabth . TEMPERATURE ;
titr 'Profile of absolute temperature' ;
evt = evol chpo tresu T li3 ;
dess evt ;
The field of temperature generated by the THERMIC procedure is written in
tabth . TEMPERATURE (or tresu). It is an object of type CHPOINT. Here the object evt contains the evolution of the component T of the CHPOINT tresu along the line li3.