Test name
ther2
Calculation type
THERMAL STEADY STATE
D AXISYMMETRICAL
Finite element type
QUA4
Topic
Test of the boundary conditions of temperature with an axisymmetrical computation.
Three different configurations are tested on a thick-walled cylinder :
Goal
Find the field of temperatures in the cylinder for each configuration.
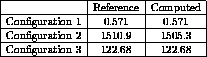
Reference
Analytical solution (1st and 2nd parts).
Comparison with results computed by THERMX (3rd part).
Version
97' customer version
Model description
CASTEM figures
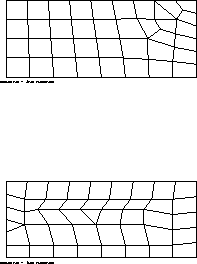
Test ther2 Results
Results
Value of the temperature at the point located on the external radius.
CASTEM figures

* Test Ther2.dgibi: Jeux de données *
* --------------------------------- *
* *
GRAPH='N';
SAUT PAGE ;
*-----------------------------------------------------*
* TEST THER2 *
* *
* TEST DES CL DE TEMPERATURE EN MODE AXISYMETRIQUE *
* ------------------------------------------------ *
* *
* TEMPERATURE IMPOSEE + CONVECTION *
* + FLUX *
* + SOURCE *
* *
* *
* Comme dans le test THER1, cet exemple permet de *
* tester les conditions aux limites de température en *
* calcul axisymétrique. *
* *
* Trois cas sont envisagés ici : *
* - un tube épais soumis à une température *
* imposée et à un flux imposé *
* - un tube épais soumis à une température *
* imposée et à une source volumique de chaleur *
* - un tube épais soumis à une température *
* imposée et à une convection forcée *
* *
*-----------------------------------------------------*
*
*--- 1er problème
* ------------
*
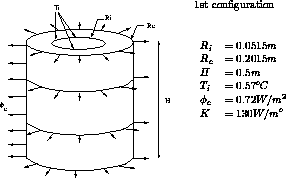
*--- Description :
*
* établir le champ de température dans un tube
* épais soumis à une condition de température
* imposée et à un flux imposé
* -----------
*--- Description de la géométrie :
*
* | axe de symétrie
* .
* | _________________________
* . | |
* . | |
* . | |
* . | |
* . | |
* . | |
* | | K=130. |
* . |_________________________| -------> R (R>0)
* | TI=0.57 F=0.72
* RI=0.0515 RE=0.2015
*
*--- Commentaires :
*
* le problème est à symétrie de révolution.
* température imposée sur la paroi interne (TI=0.57)
* flux imposé sur la paroi externe (F=0.72)
* conductibilité isotrope (K=130)
*
*--- Solution analytique :
*
* T(R) = TI + LOG(R/RI) * (F * RE)/K
* avec notammant :
* T(R=0.2015) = 0.5715225
*
*------------------------------------------------------
*
TITRE 'THER2 - C.L. TEMPERATURE - CALCUL AXISYMETRIQUE';
OPTION DIME 2 ELEM QUA4 MODE AXIS ;
OPTION ECHO 0 ;
TEMPS ;
*
*--- CREATION DE LA GEOMETRIE:
*
P1 = 0.0515 0. ;P20 = 0.0665 0. ;
P19 = 0.0665 0.5 ;P2 = 0.0515 0.5 ;
P18 = 0.0815 0. ;P17 = 0.0815 0.5 ;
P16 = 0.0965 0. ;P15 = 0.0965 0.5 ;
P14 = 0.1115 0. ;P13 = 0.1115 0.5 ;
P12 = 0.1265 0. ;P11 = 0.1265 0.5 ;
P10 = 0.1415 0. ;P9 = 0.1415 0.5 ;
P8 = 0.1565 0. ;P7 = 0.1565 0.5 ;
P6 = 0.1715 0. ;P5 = 0.1715 0.5 ;
P24 = 0.1865 0. ;P23 = 0.1865 0.5 ;
P4 = 0.2015 0.5 ;P3 = 0.2015 0. ;
*
SURF1 = MANUEL QUA4 P1 P20 P19 P2 ;
SURF2 = MANUEL QUA4 P20 P18 P17 P19 ;
SURF3 = MANUEL QUA4 P18 P16 P15 P17 ;
SURF4 = MANUEL QUA4 P16 P14 P13 P15 ;
SURF5 = MANUEL QUA4 P14 P12 P11 P13 ;
SURF6 = MANUEL QUA4 P12 P10 P9 P11 ;
SURF7 = MANUEL QUA4 P10 P8 P7 P9 ;
SURF8 = MANUEL QUA4 P8 P6 P5 P7 ;
SURF9 = MANUEL QUA4 P6 P24 P23 P5 ;
SURF10 = MANUEL QUA4 P24 P3 P4 P23 ;
SURF11 = SURF1 ET SURF2 ET SURF3 ET SURF4 ET SURF5 ET
SURF6 ET SURF7 ET SURF8 ET SURF9 ET SURF10 ;
*
SI(NEG GRAPH 'N');
TRAC SURF11 ;
FINSI;
*
D1 = DROITE 1 P1 P2 ;
D3 = DROITE 1 P3 P4 ;
*
*--- DONNEES DU PROBLEME DE THERMIQUE:
*
*--- MODELISATION:
*
MOD1 = MODL SURF11 THERMIQUE ISOTROPE ;
*
*--- CARACTERISTIQUES DU MATERIAU:
*
MAT1 = MATR MOD1 K 130. ;
*
*--- MATRICE DE CONDUCTIVITE:
*
CND1 = CONDUCTIVITE MOD1 MAT1 ;
*
*--- TEMPERATURES IMPOSEES: BLOQUE + DEPI
*
B1 = BLOQUE T D1 ;
E1 = DEPI B1 0.57 ;
*
*--- FLUX IMPOSE:
*
F1 = FLUX MOD1 0.72 D3 ;
*
*--- ASSEMBLAGE DES PREMIER ET SECOND MEMBRES:
*
RIG1 = CND1 ET B1 ;
FF1 = E1 ET F1 ;
*
*--- RESOLUTION:
*
CHTER1 = RESOUDRE RIG1 FF1 ;
TETA1 = EXTR CHTER1 T P3 ;
*
*------------------------------------------------------
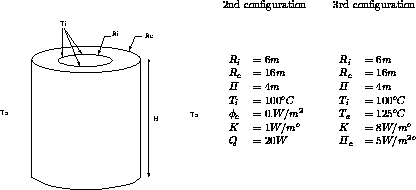
*--- - Deuxième partie - description du problème :
*
* établir le champ de température dans un tube
* épais soumis à une condition de température
* imposée ainsi qu'à une source volumique
* ----------------
*--- Description de la géométrie :
*
* | Y (axe de sym{trie)
* .
* | ______________________________
* . | |
* | | Q=20. K=1. |
* . ------------------------------ -------> X
* | TI=100. F=0.
* RI=6. RE=16.
*
*
*--- Commentaires :
*
* Le problème est à symétrie de révolution.
* Température sur la paroi interne (TI=100)
* Flux imposé sur la paroi externe (F=0)
* ( DT / DN = 0 )
* Source volumique imposée (Q=20)
* Conductibilité isotrope (K=1)
*
*--- Solution analytique :
*
* T(R) = TI - (Q/4K)*(R**2-RI**2) +
* (Q*RE/2)*RE*LOG(R/RI)
* avec notamment :
* T(R=16) = 1510.923
*
*------------------------------------------------------
*
*--- CREATION DE LA GEOMETRIE:
*
P1 = 6 0 ;
P2 = 16 0 ;
P3 = 16 4 ;
P4 = 6 4 ;
D1 = DROITE 8 P1 P2 ;
D2 = DROITE 6 P2 P3 ;
D3 = DROITE 9 P3 P4 ;
D4 = DROITE 4 P4 P1 ;
LIG1 = D1 ET D2 ET D3 ET D4 ;
SURF1 = SURFACE LIG1 PLANE ;
*
SI(NEG GRAPH 'N');
TRAC SURF1 ;
FINSI;
*
*
*--- DONNEES DU PROBLEME DE THERMIQUE:
*
*--- MODELISATION:
*
MOD1 = MODL SURF1 THERMIQUE ISOTROPE ;
*
*--- CARACTERISTIQUES DU MATERIAU:
*
MAT1 = MATR MOD1 K 1. ;
*
*--- MATRICE DE CONDUCTIVITE:
*
CND1 = CONDUCTIVITE MOD1 MAT1 ;
*
*--- TEMPERATURES IMPOSEES: BLOQUE + DEPI
*
B1 = BLOQUE T D4 ;
E1 = DEPI B1 100. ;
*
*--- FLUX IMPOSE:
*
E2 = FLUX MOD1 0. D2 ;
*
*--- SOURCE VOLUMIQUE:
*
E3 = SOURCE MOD1 20. SURF1 ;
*
*--- ASSEMBLAGE DES PREMIER ET SECOND MEMBRE:
*
RIG1 = CND1 ET B1 ;
FF1 = E1 ET E2 ET E3 ;
*
*--- RESOLUTION:
*
CHTER1 = RESOUDRE RIG1 FF1 ;
TETA2 = EXTR CHTER1 T P3 ;
*
*
*------------------------------------------------------
*
*--- Troisième partie
*
*--- Description du problème :
*
* établir le champ de température dans un tube
* épais soumis à une condition interne de tempéra-
* ture ainsi qu'à une convection sur sa paroi
* externe
*
*--- Données du problème :
*
* Conductibilité isotrope du matériau (K=8)
* Coefficient d'échange en convection (HC=5)
* Température imposée sur la paroi interne (TI=100)
* Température du milieu extérieur (TE=125)
*
*--- Solution :
*
* On pourra comparer avec les résultats suivants
* issus d'un calcul effectué par THERMX :
*
* 100.00 / 104.37 / 108.05 / 111.22 / 114.01 /
* 116.50 / 118.75 / 120.80 / 122.68
* (valeurs du champ thermique selon l'abscisse)
*
*------------------------------------------------------
*
*--- CREATION DE LA GEOMETRIE:
*
* - rayon int{reiur RI = 6.
* - rayon ext{rieur RE = 16.
* - hauteur H = 4.
* - surface interne : D4
* - surface externe : D2
*
P1 = 6 0 ;
P2 = 16 0 ;
P3 = 16 4 ;
P4 = 6 4 ;
D1 = DROITE 8 P1 P2 ;
D2 = DROITE 5 P2 P3 ;
D3 = DROITE 9 P3 P4 ;
D4 = DROITE 6 P4 P1 ;
LIG1 = D1 ET D2 ET D3 ET D4 ;
SURF1 = SURF LIG1 PLANE ;
*
SI(NEG GRAPH 'N');
TRAC SURF1 ;
FINSI;
*
*
*--- DONNEES DU PROBLEME DE THERMIQUE:
*
*--- MODELISATION:
*
MOD1 = MODL SURF1 THERMIQUE ISOTROPE ;
MOD2 = MODL D2 CONVECTION ;
*
*--- DONNEE DES CARACTERISTIQUES DU MATERIAU:
*
MAT1 = MATR MOD1 K 8. ;
MAT2 = MATR MOD2 H 5. ;
*
*--- MATRICES DE CONDUCTIVITE:
*
CND1 = CONDUCTIVITE MOD1 MAT1 ;
CNF1 = CONDUCTIVITE MOD2 MAT2 ;
*
*--- FLUX EQUIVALENTS A LA CONVECTION:
*
FF1 = CONVECTION MOD2 MAT2 T 125. ;
*
*--- TEMPERATURE IMPOSEE: BLOQUE + DEPI
*
B1 = BLOQUE T D4 ;
E1 = DEPI B1 100. ;
*
*--- ASSEMBLAGE DU PREMIER PUIS DU SECOND MEMBRE:
*
RIG1 = CND1 ET CNF1 ET B1 ;
Q1 = FF1 ET E1 ;
*
*--- RESOLUTION:
*
CHTER1 = RESOUDRE RIG1 Q1 ;
TETA3 = EXTR CHTER1 T P3 ;
*
*--- POST-TRAITEMENT
*
SAUT PAGE ;
SAUT 2 LIGN ;
MESS ' PROBLEME N›1 ' ;
MESS ' TEMPERATURE EN R = RE THEORIQUE CALCULEE ';
MESS ' T = 0.5715225 T = ' TETA1 ;
SAUT 1 LIGN ;
MESS ' PROBLEME N›2 ' ;
MESS ' TEMPERATURE EN R = RE THEORIQUE CALCULEE ';
MESS ' T = 1510.923 T = ' TETA2 ;
SAUT 1 LIGN ;
MESS ' PROBLEME N›3 ' ;
MESS ' TEMPERATURE EN R = RE REFERENCE CALCULEE ';
MESS ' T = 122.68 T = ' TETA3 ;
*
TEMPS ;
* CODE DE FONCTIONNEMENT SUR LE PROBLEME N›2
TREF=1511;RESI=ABS((TETA2-TREF)/TREF);
SI(RESI <EG 5E-2);
ERRE 0;
SINO;
ERRE 5;
FINSI;
FIN;
Test ther2 Comments
MOD1 = MODEL SURF11 THERMIQUE ISOTROPE ;
MAT1 = MATER MOD1 K 130. ;
CND1 = CONDUCTIVITE MOD1 MAT1 ;
The thermic model (MOD1) is defined with the formulation named THERMIQUE ISOTROPE. This model is described by the geometry SURF11, the conductivity of the model is defined with the operator MATER.
The operator COND(UCTIVITE) builds the matrix of conductivity (CND1).
B1 = BLOQUE T D1 ;
E1 = DEPI B1 0.57 ;
F1 = FLUX MOD1 ;
The operator BLOQUE builds the boundary condition (B1) on the degree of freedom T of the line D1. The operator DEPI(MPOSE) imposes a value of 0.57 on the condition B1.
The operator FLUX imposes a flux of 0.72 on the line D3 which belongs to MOD1.
The first and second members of the equation to be solved are gathered and the computation is performed with the operator RESO. The computed object CHTER1 is a CHPOINT type and the values of its component T can be extracted with the operator EXTR(AIRE).
E3 = SOURCE MOD1 20. SURF1 ;
The model, the imposed temperature and the flux are defined in the same way as in the first configuration.
The operator SOURCE defines an imposed volumetric source of heat on the surface SURF1.
The computation is performed like in the first problem by gathering first and second members of the equation and then by solving with the RESO operator.
MOD1 = MODEL SURF1 THERMIQUE ISOTROPE ;
MOD2 = MODEL D2 CONVECTION ;
**
MAT1 = MATER MOD1 K 8. ;
MAT2 = MATER MOD2 H 5. ;
**
CND1 = CONDUCTIVITE MOD1 MAT1 ;
CNF1 = CONDUCTIVITE MOD2 MAT2 ;
**
FF1 = CONVECTION MOD2 MAT2 T 125. ;
The outer surface is submitted to forced convection : as the problem is axisymmetrical, the outer surface is modelled by the line D2. Along this line is defined a convection model (MOD2) by using the operator MODEL followed by the formulation CONVECTION.
The operator MATER defines the convection exchange coefficient.
The operator CONV(ECTION) imposes a condition of convection on the structure defined in the objects MOD2 and MAT2, it is necessary to indicate the value of the external temperature (T=125).