Test name
dyna11
Calculation type
MECHANICS DYNAMICS 2D
Finite element type
QUA4
Topic
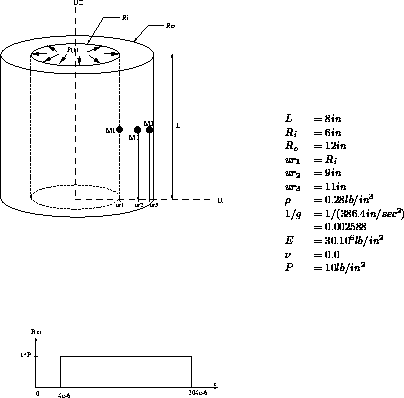
Transient response of an internal pressure.
A thick-walled cylinder is suddenly subjected to an internal pressure. The problem consists in finding displacement maxima of some points.
Goal
Find displacement maxima of three points located on the cylinder half-length.
Reference
S. H.Crandall, N. C. Dahl and T. J. Lardner : An introduction to the mechanics of solids, 2nd ed. (New York : McGraw-Hill Book Company, 1972) pp. 293-297.
Version
97' customer version
Model description
Test dyna11 Results
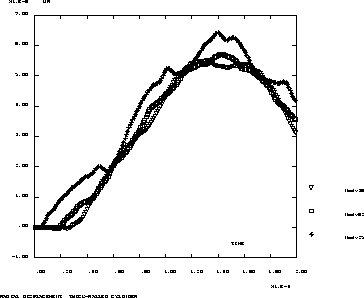
Results : Ratio transient/static
CASTEM figures
* Test Dyna11.dgibi: Jeux de données *
* ---------------------------------- *
* *
GRAPH='N';
SAUT PAGE ;
*******************************************************
* REPONSE TRANSITOIRE A UNE PRESSION INTEREN
*******************************************************
*
* DESCRIPTION DU PROBLEME
* ------------------------
* UN CYLINDRE A PAROIS EPAISSES EST SOUMISE BRUTALEMENT
* A UNE PRESSION INTERNE . IL S 'AGIT DE TROUVER LES
* PICS DES DEPLACEMENTS DANS CERTAINS POINTS DE LA
* STRUCTURE EN QUESTION .
*
* REFERENCE :
* ----------
* S. H. CRANDALL,N.C. DAHL,AND T. J. LARDNER ,AN
* INTRODUCTION TO THE MECHANICS OF SOLIDS,2ND ED.
* (NEW YORK :MCGRAW-HILL BOOK COMPANY,1972) PP. 293-297
*******************************************************
OPTION ECHO 0 ;
OPTIO DIME 2 MODE AXIS ELEM QUA4 ;
*
* MAILLAGE
*
P1 = 6. 0. ; P2 = 12. 0. ; P3 = 12. 8. ; P4 = 6. 8. ;
L1 = D 6 P1 P2 ; L2 = D 8 P2 P3 ;L3 = D 6 P3 P4 ;
L4 = D 8 P4 P1 ; LTOT = L1 ET L2 ET L3 ET L4 ;
S1 = SURF LTOT PLAN ;
*
* MODELE
*
MOD1 = MODELE S1 MECANIQUE ELASTIQUE ;
*
* PROPRIETES DE MATERIAUX
*
RO = 0.28 * 0.002588 ;
MAT1 = MATER MOD1 YOUN 30.E6 NU 0.0 RHO RO ;
*
* CONDITIONS AUX LIMITES
*
CL1 = BLOQ L1 UZ ;CL2 = BLOQ L3 UZ ;
*
* MATRICE DE RIGIDITE
*
RIG1 = RIGIFITE MOD1 MAT1 ;
*
* MATRICE DE MASSE
*
MAS1 = MASSE MOD1 MAT1 ;
*
* CHARGEMENT
*
LI1 = (PROG 0. 1.E-6 2.E-6 3.E-6 4.E-6 ) ET
(PROG 5e-6 pas 1e-6 204E-6 );
LI2 = (PROG 0. 0. 0. 0. 0. ) ET (PROG 200 * 1.) ;
F1 = PRES MOD1 'MASS' 10. L4 ;
EV = EVOL MANU T LI1 F(T) LI2 ;
CHA1 = CHAR 'PRES' F1 EV ;
*
* PREPARATION DE LA TABLE DE DONNEES POUR DYNAMIC
*
LIS1 = PROG 0. PAS 1.E-6 200.E-6 ;
TAB2 = TABLE ;
TAB2.'DEPL' = MANU CHPO S1 2 UZ 0. UR 0. ;
TAB2.'VITE' = MANU CHPO S1 2 UZ 0. UR 0. ;
TAB2.'CHAR' = CHA1 ;
TAB2.'RIGI' = RIG1 ;
TAB2.'MASS' = MAS1 ;
TAB2.'FREQ' = 250000. ;
TAB2.'INST' = LIS1 ;
TAB1 = DYNAMIC TAB2 ;
*
* EXTRAIRE LES OBJETS D'EVOLUTION DE DEPLACEMENTS
*
LT = PROG ; LUR1 = PROG ;
LUR2 = PROG ;
LUR3 = PROG ;
I = 0 ;
M1 = NOEUD 25 ;M2 = NOEUD 62 ; M3 = NOEUD 36 ;
NBB = (DIME LIS1) - 1 ;
REPETER BB1 NBB ;
I = I + 1 ;
LT = LT ET( PROG(TAB1 . I . 'TEMP' ));
DEP1 = TAB1 . I . 'DEPL' ;
LUR1 = LUR1 ET( PROG (EXTR DEP1 UR M1) );
LUR2 = LUR2 ET( PROG (EXTR DEP1 UR M2) );
LUR3 = LUR3 ET( PROG (EXTR DEP1 UR M3) );
FIN BB1 ;
EV1 = EVOL MANU 'TIME' LT 'UR ' LUR1 ;
EV2 = EVOL MANU 'TIME' LT 'UR ' LUR2 ;
EV3 = EVOL MANU 'TIME' LT 'UR ' LUR3 ;
*
* --- TRACER LES COURBES
*
TABDD = TABLE ;
TABDD.1 = 'MARQ ETOI NOLI ' ;
TABDD.2 = 'MARQ CARR NOLI ' ;
TABDD.3 = 'MARQ TRIA NOLI ' ;
TABDD.'TITRE' = TABLE ;
TABDD.'TITRE'. 1 = MOT 'N 25' ;
TABDD.'TITRE'. 2 = MOT 'N 62' ;
TABDD.'TITRE'. 3 = MOT 'N 36' ;
'TITR' 'RADIAL DISPLACEMENT THICK-WALLED CYLINDER ' ;
SI (NEG GRAPH 'N');
DESS (EV1 ET EV2 ET EV3) TABDD 'LEGE' ;
FINSI ;
*
* COMPARAISON AVEC LA THEORIE
*
UR1 = (MAXI LUR1) / 3.326E-6 ; UR1TH = 2. ;
ERR1 = ((UR1 - UR1TH) / (ABS UR1TH)) * 100. ;
UR2 = (MAXI LUR2) / 2.773E-6 ; UR2TH = 2. ;
ERR2 = ((UR2 - UR2TH) / (ABS UR2TH)) * 100. ;
UR3 = (MAXI LUR3) / 2.673E-6 ; UR3TH = 2. ;
ERR3 = ((UR3 - UR3TH) / (ABS UR3TH)) * 100. ;
MESS
'RAPPORT TRANSITOIRE / STATIQUE ' ;
MESS
'NODE 25 THEORIE 'UR1TH 'CASTEM ' UR1 '%ERREUR 'ERR1;
MESS
'NODE 62 THEORIE 'UR2TH 'CASTEM ' UR2 '%ERREUR 'ERR2;
MESS
'NODE 36 THEORIE 'UR3TH 'CASTEM ' UR3 '%ERREUR 'ERR2;
*
SI ((MAXI ABS (PROG ERR1 ERR2 ERR3 )) < 5);
ERRE 0;
SINON;
ERRE 5;
FINSI;
FIN ;
Test dyna11 Comments
RO = 0.28 * 0.002588 ;
MAT1 = MATER MOD1 YOUN 30.E6 NU 0.0 RHO RO ;
There is no unit system on CASTEM. Therefore data must be given in a right system according to the basic law of mechanics :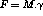 
.
It is necessary here to give the density in mass per volume unit that is to say to divide the density (given in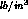 
) by the acceleration constant g (given in 
).
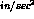LT = PROG ; LUR1 = PROG ;
...
I = 0 ;
M1 = NOEUD 25 ;
...
NBB = (DIME LIS1) - 1 ;
REPETER BB1 NBB ;
I = I + 1 ;
LT = LT ET( PROG(TAB1 . I . 'TEMP' ));
DEP1 = TAB1 . I . 'DEPL' ;
LUR1 = LUR1 ET( PROG (EXTR DEP1 UR M1) );
...
FIN BB1 ;
EV1 = EVOL MANU 'TIME' LT 'UR ' LUR1 ;
To get the displacement evolution as a function of time, it is necessary to extract each saved instant and store it in a list of reals (LT). In the same way, each saved UR-displacement of the required point is stored in the LUR1 list of reals. Then an object of EVOLUTION type (EV1) can be obtained which represents the UR-displacement of M1 point as a function of time.
TABDD = TABLE ;
TABDD.1 = 'MARQ ETOI NOLI TITR Node25' ;
TABDD.2 = 'MARQ CARR NOLI TITR Node62' ;
TABDD.3 = 'MARQ TRIA NOLI TITR Node36' ;
TITR 'RADIAL DISPLACEMENT THICK-WALLED CYLINDER ' ;
DESS (EV1 ET EV2 ET EV3) TABDD 'LEGE' ;
To get a caption the LEGE keyword is added to the DESS operator, but it is necessary to indicate some specific options. These options are defined in the
TABDD table. Each index of the table correspond to one curve : TABDD.1 is related to the first curve indicated in the DESS call.
The MARQ keyword followed by ETOI indicates that a symbol (a star) will be plotted as a marker at different points of the curve (CARR correspond to squares, TRIA correspond to triangles).
NOLI indicates that the segments connecting the points won't be plotted.
The TITR keyword followed by a string (maximum 20 letters and no gap between letters) defines the caption related to the required curve.