Test name
vibr6
Calculation type
MECHANICS DYNAMICS 3D
COMPOUND EIGEN SHAPES
Finite element type
TUYA
Topic
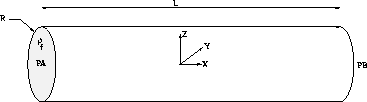
Compound eigen modes of a rod.
The rod is subjected to an external axial permanent flow. Both the tips of the rod are articulated.
Computations are made for different flow velocities (0 up to 120 m/s).
Goal
Find the real and imaginary parts of frequencies for the different velocities.
Reference
Model of Paidoussis & Ortoja-Starzewski.
Version
97' customer version
Model description

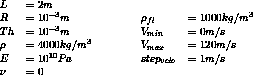
Test vibr6 Results
Results
Velocity V = 0

Velocity V = 120 m/s
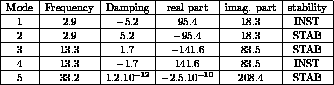
CASTEM figures
* Test Vibr6.dgibi: Jeux de données *
* --------------------------------- *
* *
**************************************************
* TEST : VIBR6 *
* *
* Modele de PAIDOUSSIS & ORTOJA-STARZEWSKI *
* *
* On recherche ici les modes propres *
* complexes d'un arbre soumis a un ecoulement *
* Arbre soumis a un ecoulement exterieur *
* axial permanent *
* Conditions aux limites : articule - articule *
**************************************************
*
Opti Echo 0;
*
*--- Affichage
AFFICH = VRAI;
GRAPH = 'N';
IMPRPS = FAUX;
*
*Si (NON AFFICH);
* Opti Echo 1;
*Finsi;
Si (IMPRPS);
Opti Trac ps;
Finsi;
************************************
* Caracteristiques du systeme *
************************************
*--- Materiau
Rhostru = 4000.;
Youstru = 1.E10;
Nustru = 0.;
*--- Longueur du crayon
Lstru = 2.;
*--- Rayon du crayon
R = 10.E-3;
*--- Section du crayon
Sstru = PI*R*R;
*--- Masse lineique du crayon
Mstru = Rhostru*Sstru;
*--- Masse volumique du fluide
Rhof = 1000.;
*--- Masse ajoutee du fluide (fluide non confine)
Mfaj = Rhof*PI*R*R;
*--- Masse volumique equivalente
Rhoe = (Mstru+Mfaj)/Sstru;
*--- Vitesse axiale du fluide
Vmin = 0.;
Vmax = 120.;
PVa = 1.;
*
LVa = Prog Vmin PAS PVa Vmax;
*
**************************************
* Maillage du systeme *
**************************************
*
NbN = 100;
Mess 'Nombre de noeuds :' NbN;
Mess ' ';
Opti Dime 3 Elem Seg2;
PA = (-.5*Lstru) 0. 0.;
PB = (.5*Lstru) 0. 0.;
L1 = Droi NbN PA PB;
*
Modl1 = Modl L1 Mecanique Elastique Isotrope Tuya;
Matr1 = Matr Modl1 Youn Youstru Nu Nustru Rho Rhoe
Epai R Rayo R;
*
**************************************
* Masses, Rigidites ... du systeme *
**************************************
*
*--- Masse
Mstru = Masse Modl1 Matr1;
*--- Raideur structrale
Kstru = Rigi Modl1 Matr1;
*--- Conditions aux limites : Probleme plan
Cl1 = Bloq Ux L1;
Cl2 = Bloq Uy L1;
Cl3 = Bloq Rx L1;
Cl4 = Bloq Rz L1;
Cl5 = Bloq Uz (PA et PB);
*
Kstru = Kstru et Cl1 et Cl2 et Cl3 et Cl4 et CL5;
*
***********************************
* Rigidites supplementaires *
***********************************
*
Lpout = Lstru/NbN;
*
*--- Amortissement du a l'écoulement
PAfu =
(Prog -.5 0. 0. (Lpout/10.) .5 0. 0. (-1.*Lpout/10.) );
PAfu = PAfu et
(Prog 0. -.5 (-1.*Lpout/10.) 0. 0. .5 (Lpout/10.) 0.);
PAfu = PAfu et
(Prog 0. (Lpout/10.) 0. 0. 0. (-1.*Lpout/10.)
(-1.*Lpout*Lpout/60.) 0.);
PAfu = PAfu et
(Prog (-1.*Lpout/10.) 0. 0. 0. (Lpout/10.) 0. 0.
(-1.*Lpout*Lpout/60.));
PAfu = PAfu et
(Prog -.5 0. 0. (-1.*Lpout/10.) .5 0. 0. (Lpout/10.) );
PAfu = PAfu et
(Prog 0. -.5 (Lpout/10.) 0. 0. .5 (-1.*Lpout/10.) 0. );
PAfu = PAfu et
(Prog 0. (-1.*Lpout/10.) (Lpout*Lpout/60.) 0. 0.
(Lpout/10.) 0. 0. );
PAfu = PAfu et
(Prog (Lpout/10.) 0. 0. (Lpout*Lpout/60.)
(-1.*Lpout/10.) 0. 0. 0. );
Afu = Manu Rigi type AMORTISSEMENT L1
(MOTS UY UZ RY RZ) PAfu;
*
*--- Raideur due a l'ecoulement
PKfu =
(Prog (-6./(5.*Lpout)) 0. 0. -1.1 (6./(5.*Lpout)) 0. 0.
-.1);
PKfu = PKfu et
(Prog 0. (-6./(5.*Lpout)) 1.1 0. 0. (6./(5.*Lpout)) .1
0.);
PKfu = PKfu et
(Prog 0. .1 (-2.*Lpout/15.) 0. 0. -.1 (Lpout/30.) 0. );
PKfu = PKfu et
(Prog -.1 0. 0. (-2.*Lpout/15.) .1 0. 0. (Lpout/30.) );
PKfu = PKfu et
(Prog (6./(5.*Lpout)) 0. 0. .1 (-6./(5.*Lpout)) 0. 0.
1.1);
PKfu = PKfu et
(Prog 0. (6./(5.*Lpout)) -.1 0. 0. (-6./(5.*Lpout))
-1.1 0. );
PKfu =
PKfu et (Prog 0. .1 (Lpout/30.) 0. 0. -.1
(-2.*Lpout/15.) 0. );
PKfu = PKfu et
(Prog -.1 0. 0. (Lpout/30.) .1 0. 0. (-2.*Lpout/15.) );
Kfu = Manu Rigi type RIGIDITE L1 (MOTS UY UZ RY RZ)
PKfu;
*
*
*****************************************
* Analyse modale *
*****************************************
*
PMod = Prog 2.77 11.1 24.99 44.43 69.42;
Basr = VIBR PROCH PMod Kstru Mstru TBAS;
nnor (Basr.'MODES') (mots 'UZ');
*
Basm = Basr.'MODES';
Nbmod = DIME Basm-2;
Si (Affich);
Mess ' ';
Mess 'Fluide a l arret';
Mess ' Mode Frequence ';
Mess '---------------------------';
Repeter LMod Nbmod;
i=&LMod;
Mess ' ' i ' ' Basm.i.'FREQUENCE';
Fin LMod;
Mess ' ';
Mess ' ';
Mess ' ';
Finsi;
*
*****************************************
* Mise en forme du tableau de resultats *
*****************************************
*
Mod = Table;
Mod.Reel = Table;
Mod.Imag = Table;
Repeter Bloc6 (2*Nbmod);
i=&Bloc6;
Mod.Reel.i=Prog;
Mod.Imag.i=Prog;
Fin Bloc6;
*
*****************************************
* Projection des matrices *
*****************************************
*
*--- Matrice masse
Mt = (PJBA MStru Basr);
*--- Matrices amortissement
Afp = (PJBA Afu Basr);
*--- Matrices de raideur
Ksp = (PJBA Kstru Basr);
Kfp = (PJBA Kfu Basr);
*
*--- Reperage de la vitesse critique
VSauv = 'N';
* ===================================== *
* Boucle sur la vitesse axiale *
* ===================================== *
*
Repeter Bloc10 (DIME LVa);
k=&Bloc10;
Va = Extr LVa k;
Si (AFFICH);
Mess 'Iteration' k;
Mess 'Vitesse axiale : ' Va ;
Mess ' ';
Mess '----------------------------------------------------------------
--------------';
Mess ' Mode Frequence Amort. P. Reelle P. Imaginaire
Stabilité ';
Finsi;
*
******************************************
* Masses, rigidites ... *
******************************************
*
*---- Amortissement
At = (2*Mfaj*Va*Afp);
*---- Rigidite
Kt = (Ksp) et ((Mfaj*Va*Va)*Kfp);
*
******************************************
* Calcul des modes complexes *
******************************************
*
Basc = VIBC Mt Kt At;
Basm = Basc.'MODES';
*
*--- Extraction des frequences
Prf = Prog;
Pif = Prog;
Repeter Bloc2 (2*Nbmod);
i=&Bloc2;
Modn = Basm.i;
f = Modn.'FREQUENCE_REELLE';
* Si (>EG f 0.);
Prf = Prf et (Prog Modn.'FREQUENCE_REELLE');
Pif = Pif et (Prog Modn.'FREQUENCE_IMAGINAIRE');
* Finsi;
Fin bloc2;
*
*--- Tri croissant des frequences
n1 = DIME Prf;
Prfc = Prog (extr Prf 1);
Pifc = Prog (extr Pif 1);
Repeter Bloc3 (n1-1);
i=&Bloc3+1;
f = extr Prf i;
n2 = DIME Prfc;
Pos = 1;
Repeter Bloc4 n2;
j = &Bloc4;
f1 = extr Prfc j;
Si (> f f1);
Pos = Pos + 1;
Finsi;
Fin Bloc4;
Prfc = INSE Prfc Pos f;
Pifc = INSE Pifc Pos (extr Pif i);
Fin Bloc3;
*--- Sauvegarde
Repeter Bloc5 n1;
i=&Bloc5;
f = (Extr Prfc i);
if = (Extr Pifc i);
Si (AFFICH);
Msg = 'STAB.';
Si ((< if -1.D-10) et (>EG f 0.));
Msg = 'INST.';
Si (EGA VSauv 'N');
Vcrit = Va - (PVa/2.);
VSauv = 'O';
Finsi;
Finsi;
Si (> f 0.);
*Valeurs propres relatives a lambda = i omega = ix2PIxf
Mess i f (if/f) (-2*PI*if) (2*PI*f) Msg;
Sinon;
Si (EGA f 0.);
Mess i f
' ----- ' (-2*PI*if) (2*PI*f) Msg;
Finsi;
Finsi;
Finsi;
Mod.Reel.i = Mod.Reel.i et (Prog f);
Mod.Imag.i = Mod.Imag.i et (Prog if);
Fin Bloc5;
Si (AFFICH);
Mess '----------------------------------------------------------------
--------------';
Mess ' ';
Finsi;
*
Fin Bloc10;
*
**********************************
* Traces *
**********************************
*
*
Si ( EGA GRAPH '0');
*
Nbcour=2*Nbmod;
Tab1 = Table;
Repeter Ident1 Nbcour;
k=&Ident1;
Tab1.k = 'NOLI';
Fin Ident1;
*
k=1;
*--- Traces relatifs a la frequence
Titr 'Frequences (partie reelle)';
Evol1 = Evol BLAN manu Lva (Mod.Reel.k);
Titr 'Frequences (partie imaginaire)';
Evol2 = Evol BLAN manu Lva (Mod.Imag.k);
Titr 'Lambda (partie reelle)';
*--- Traces relatifs a lambda = i 2 Pi f
Evol3 = Evol BLAN manu Lva (-2.*PI*(Mod.Imag.k));
Titr 'Lambda (partie imaginaire)';
Evol4 = Evol BLAN manu Lva (2*PI*(Mod.Reel.k));
Titr 'Lambda (partie reelle / partie imaginaire)';
Evol5 = Evol BLAN manu (2.*PI*(Mod.Reel.k))
(-2.*PI*(Mod.Imag.k));
Repeter Trac1 (Nbcour-1);
k=&Trac1+1;
Si (> (DIME Mod.Reel.k) 0);
Titr 'Frequences (partie reelle)';
Evol1 = Evol1 et (Evol BLAN manu Lva (Mod.Reel.k));
Titr 'Frequences (partie imaginaire)';
Evol2 = Evol2 et (Evol BLAN manu Lva (Mod.Imag.k));
Titr 'Lambda (partie reelle)';
Evol3 = Evol3 et (Evol BLAN manu Lva
(-2.*PI*(Mod.Imag.k)));
Titr 'Lambda (partie imaginaire)';
Evol4 = Evol4 et (Evol BLAN manu Lva
(2.*PI*(Mod.Reel.k)));
Titr 'Lambda (partie reelle / partie imaginaire)';
Evol5 = Evol5 et (Evol BLAN manu
(2.*PI*(Mod.Reel.k)) (-2.*PI*(Mod.Imag.k)));
Finsi;
Fin Trac1;
Dess Evol1 XBOR 0. 150. YBOR 0. 70. Lege
Titx 'Vax (m/s)'
Tity 'Re(F) (Hz)' Tab1;
Dess Evol2 Lege
Titx 'Vax (m/s)'
Tity 'Im(F) (Hz)' Tab1;
Dess Evol3 XBOR 0. 150. YBOR -150. 150. Lege
Titx 'Vax (m/s)'
Tity 'Re(i2.PI.F)' Tab1;
Dess Evol4 XBOR 0. 150. YBOR 0. 450. Lege
Titx 'Vax (m/s)'
Tity 'Im(i2.PI.F)' Tab1;
Dess Evol5 XBOR 0. 500. YBOR -150. 150. Lege
Titx 'Re(i2.PI.F)'
Tity 'Im(i2.PI.F)' Tab1;
Finsi;
*
**********************************
* Test de bon fonctionnement *
**********************************
*
Vth = (Pi/Lstru)*((Youstru*Pi*(R**4)/(4*mfaj))**0.5);
*Mess 'Erreur : ' (Abs((Vcrit-Vth)/Vth));
*Opti donn 5;
Si (Abs((Vcrit-25.)/25.) < 0.05);
Erre 0;
Sinon;
Erre 5;
Finsi;
*
FIN;
Test vibr6 Comments
Afu = Manu Rigi type AMORTISSEMENT L1 (MOTS UY UZ RY RZ) PAfu;
Kfu = Manu Rigi type RIGIDITE L1 (MOTS UY UZ RY RZ) PKfu;
The operator MANU followed by RIGI keyword creates a RIGIDITE subtype object in which all elementary stiffness matrices are similar :
- the elementary matrix is given by a list of reals (PAfu and PKfu),
- the geometrical object is given by L1,
- the type of stiffness is specified (AMORTISSEMENT and RIGIDITE),
- the name of the components for each node of L1 is given by a list of words (MOTS UY UZ RY RZ).
In this case, each elementary matrix is defined by a 8X8 matrix : 2 x (UY UZ RY RZ).
* Mass matrix
Mt = (PJBA MStru Basr);
** Damping matrices
Afp = (PJBA Afu Basr);
** Rigidity matrices
Ksp = (PJBA Kstru Basr);
Kfp = (PJBA Kfu Basr);
The PJBA operator calculates the projection of stiffness objects (MStru, Afu, Kstru and Kfu) on an eigen mode basis (Basr).
Basc = VIBC Mt Kt At;
Basm = Basc.'MODES';
...
Modn = Basm.i;
Prf = Prf et (Prog Modn.'FREQUENCE_REELLE');
Pif = Pif et (Prog Modn.'FREQUENCE_IMAGINAIRE');
VIBC computes the complex eigen values and eigen vectors of the general equation : 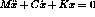 .
.
The mass (Mt), stiffness (Kt) and damping (At) are given in matrices previously expressed relatively to a real eigen mode basis. If these matrices have not their subtypes corresponding with MASSE, RIGIDITE and AMORTISSEMENT, the input order is very important because they can't be sorted: they then are processed in order of their input.
The generated object is a BASE_MODALE subtype table (Basc).
Basc.'MODES' is a BASE_DE_MODES subtype table (Basm).
Basm.i is a MODE_COMPLEXE subtype table (Modn) :
Modn.'FREQUENCE_REELLE' : real part of the eigen frequency.
Modn.'FREQUENCE_IMAGINAIRE' : imaginary part of the eigen frequency.
Modn.'NUMERO_MODE' : number of the mode.
Modn.'DEFORMEE_MODALE_REELLE' : real part of the eigen vector.
Modn.'DEFORMEE_MODALE_IMAGINAIRE' : imaginary part of the eigen vector.
Dess Evol1 XBOR 0. 150. YBOR 0. 70. Lege
Titx 'Vax (m/s)' Tity 'Re(F) (Hz)' Tab1;
The XBOR and YBOR keywords impose boundaries on X-axis (mini 0. and maxi 150.) and on Y-axis (mini 0. and maxi 70.).
The LEGE keyword imposes a caption for the different plotted curves. It imposes a square frame and the maximal number of curves is nine.
The TITX and TITY keywords allow to modify the names of abscissas and ordinates.