Test precont2 Description sheet

Test name

Calculation type

Finite element type

Topic

The structure is a reinforced concrete beam. The reinforcement is made of tendon. The beam is subjected to pressure on its upper surface, and embedded from its lower side.

Goal

Reference

Version

Model description

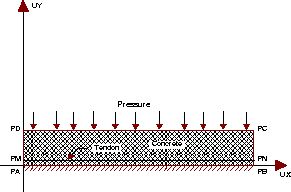
Test precont2 Results

CASTEM FIGURES

*         Test Precont2.dgibi: Jeux de données        *
*         ------------------------------------        *
*                                                     *
*---------------------------------------------------*
* CALCUL AVEC ARMATURE ACTIVE.
* PROGRAMME DE VERIFICATION DE :
*    - PREC
*    - EQUI FORC
*---------------------------------------------------*
*  
*---------------------------------------------------*
titr 'precont2.dgibi';
opti echo 1;
graph='n'    ;
opti dime 2 elem qua4 mode plan;
* 
* GEOMETRIE
*
long = 10.0;
*---BETON
h = 1. ;
h1= .9 ;
*h1 = 1. -  (1./6.1);
pa=0.0 0.0;
pb=long 0.0;
pc=long h.;
pd=0.0 h;pn = 0. (h - h1)  ;
nb1=40;
nb2=6;


c1=pa droi nb1 pb; 
c2=pb droi nb2 pc; 
c3=pc droi nb1 pd; 
c4=pd droi nb2 pa; 
sur1=dall c1 c2 c3 c4;
*---ARMATURE
pm = long (h - h1)  ;
pn = 0.   (h - h1)  ;
*nca = 20 ;
 nca = 17 ;
d1 = pm droi nca pn;
* d1 = pn droi nca pm;
*---GEOMETRIE TOTALE

si(neg graph 'n');
 titr 'massif' ( sur1 nbel ) 'cable initial' (d1 nbel);
 trac elem ( sur1 et d1) ;
finsi;
*
* MODELE
*
modb=modl sur1 mecanique elastique;
d2 = (kabl sur1 d1 ) coul roug ;
mod1 = modl d1 mecanique elastique armature barr;
mod2 = modl d2 mecanique elastique armature barr;
d5= sur1 et d2 ;
si(neg graph 'n');
 titr 'Maillage armature apres KABL' (d2 nbel) ;
 trac d2 elem   ;

finsi;
*
* CARACTERISTIQUES DU BETON
*
Eb = 0.4e11 ;
matb=matr modb youn Eb nu 0.0;
Ea = 2.0e11 ;ssect = .02 ;

*   TENSION DU CABLE 
SIG0 = 1200.E6 ; tens = sig0 * ssect ;
    
mat2= (mate mod2 youn Ea ) et ( cara mod2 sect ssect );

*     Pour la methode accro on definit                *
*     un materiau sur le renfort initial              * 
  
mat1= (mate mod1 youn Ea ) et ( cara mod1 sect ssect );
*
* CONDITIONS AUX LIMITES
*
cl1 = bloq pa ux;
cl2 = bloq pa uy;
cl3 = bloq pb uy;
cl4 = rela ense ux c2;
cl5 = rela ense ux c4;
cltot = cl1 et cl2 et cl3 ;
*


*
* CHARGEMENT
TA = TABLE ;
TA . FPRG = 0. ;
pre1=(prec mod2 mat2 tens TA  pm)  ;
si ( neg graph 'n') ;
titre 'Precontaintes sans pertes  (mprecont20.dgibi) ';
ev1 = evol roug chpo ( chan chpo pre1 mod2) EFFX  
      ( inve d2) ;
dess ev1 ;
finsi ;

 chac = -1 * (bsig pre1 mod2 mat2) ;
 cha1 = -1 * (equiv forces modb mod2 pre1 );

 rchac = resu chac ; 
 rcha1 = resu cha1 ; 
list rchac ;
list rcha1 ;
faccro = (redu chac pm) resu abs maxi ;                           
faequi = (redu cha1 c2) resu abs maxi ;

err1 = abs(((faequi - tens )/tens)*100) ;
err2 = abs(((faccro - tens )/tens)*100) ;

*---Code de bon fonctionnement
si ((err1 < 1.) et ( err2 < 1.))  ;
   erre 0 ;
sinon ;
   erre 5 ;
finsi ;


   
si(neg graph 'n');

uu = maxi ( abs chac) avec ( mots FX) ;
ampv = 2./uu ;
TITRE ' resultante chargement bsigma '  faccro ;
vvbsi = vecteur chac FX FY  ampv   vert ;
trac sur1 vvbsi ;
vvv   = vecteur cha1 FX FY  ampv  vert ;
TITRE ' resultante chargement equiv prec ' faequi  ; 
trac sur1 vvv ;
finsi;

*
* RESOLUTION BETON SOUS PRECONTRAINTE
*
*---resolution
 rib = rigi modb matb;
     mt = matb et mat2    ;
     raeq = equi rigi modb mod2 mt ;
     
     depequi = reso (rib  et cltot ) cha1;
*  rik est la raideur  des cables  pour modele accro 
     rik = rigi mod1 mat1 ;
     racc = rela d2 ACCROCHER sur1 ; 
     depacc = reso (rib  et racc  et cltot ) chac;
 
*----------trace de la deformee
uma1 = maxi depequi avec ( mots UY) ;
uma2 = maxi depacc avec  ( mots UY) ;


*---Code de bon fonctionnement

err10 = abs(((uma1 - uma2)/uma1)*100) ;

si  ( err10 < 1. ) ;
   erre 0 ;
sinon ;
   erre 5 ;
finsi ;


amp1 = .2/uma1 ;
de0=deform (sur1 et d2) depequi 0.  blan;

dep0a = proi d2 (chan  cham  depequi  modb NOEUDS) ;
dep0b = proi d2 (chan  cham  depacc   modb NOEUDS) ;

de1=deform sur1 depequi amp1 bleu ;

de2 = deform sur1 depacc amp1 bleu ;

de1a=deform d2 dep0a amp1 vert ;
de1b=deform d2 dep0b amp1 turq ;
  
*   CACLUL DES  PRECONTRAINTES BETON ' ;

si(neg graph 'n');

 titr ' precontrainte equi uy max = ' uma1 
      ' tension cable '  faequi ;
 trac (de0 et de1 et de1a);
 titr ' precontrainte accr uy max = ' uma2 
      ' tension cable '  faccro ;
 trac ( de0 et de2 et de1b) ;

finsi;


***  AJOUT  D'UNE CHARGE SUR LA FACE SUPERIEURE     ***
 b= 1.;
 X = ((h*h*Eb )+ (2*h1*Ea*ssect))/
     ((2*h*Eb)+(2*Ea*ssect)) ;
 ii = (((x**3) + ((h-x)**3))/3 )+((Ea*ssect*(h1-x)*
      (h1-x))/Eb);
 prsup = press mass modb c3 2.e6;
 FTS = 2.E6 * long ;
 
*----------- FLECHE ANALYTIQUE SANS PRECONTRAINTE
  dmax = 5.*FTS*(long**3)/(384*Eb*ii) ;
  mess ' fleche analytique  ' dmax ;
  
* ----------  CALCUL PAR EQUI RIGI   ET    RELA ACCRO 
  
dep2equi = reso ( rib et  raeq  et cltot       ) prsup;
dep2accr = reso ( rib et  racc  et rik et cltot) prsup; 
uyma1 =  mini dep2equi  avec ( mots uy) ;
uyma2 =  mini dep2accr avec ( mots uy) ;
amp = .2/(abs uyma1) ;

*---Code de bon fonctionnement
err1 = abs(((uyma1 + dmax )/dmax)*100) ;
err2 = abs(((uyma2 + dmax )/dmax)*100) ;

si ( ( err1 <  1.  ) et ( err2  <  1.   ) ) ;
   erre 0 ;
sinon ;
   erre 5 ;
finsi ;

  
defequi=deform sur1 dep2equi amp rouge;
defaccr=deform sur1 dep2accr amp rouge;

si(neg graph 'n');
 titr ' force repartie / equiv uy max = ' uyma1 
      ' analytique ' dmax ; 
 trac (de0 et defequi );
 titr ' force repartie / accro uy max = ' uyma2 
      ' analytique ' dmax ; 
 trac (de0 et defaccr );
finsi;


* MEME PRECONTRAINTE AVEC PERTE DE 
*    PRECONTRAINTE DUE AU FROTTEMENT
*  S = So * (1 - exp(-ff*alpha-phif*x))
*
*--- avec ff = 0.18 et phif = 0.002
    mat2=(mate mod2 youn 2.0e11 ff 0.18 phif 0.2 
         ganc 0.00 rmu0 0.43 fprg 1700.e9 rh10 2.5 )
         et ( cara mod2 sect .02 ) ; 


pre2= (prec mod2 mat2 tens pm) ;
cha2 = -1 * (equiv forces modb mod2 pre2 );
chac = -1 * (bsig pre2 mod2 mat2) ;
uu = maxi ( abs cha2) avec ( mots FX) ;
ampv = 2./uu ;

si ( neg graph 'n' ) ;
titre 'Precontaintes avec pertes  (mprecont20.dgibi) ';
ev2 = evol roug chpo ( chan chpo pre2 mod2) EFFX  
      ( inve d2) ;
dess ev2 ;
vv2   = vecteur cha2 FX FY  ampv  vert ;
TITRE '  chargement avec pertes de precontrainte '   ; 
trac sur1 vv2 ;

finsi ;
*------------    DEFORMATIONS INITIALES ---------------
 

  depert1  = reso (rib  et cltot ) cha2;
  depert2  = reso (rib  et racc et cltot ) chac ;
  
  de1p=deform sur1 depert1 amp1 bleu ;
  de2p=deform sur1 depert2 amp1 vert ;
  
  
  uma3 = maxi depert1 avec ( mots UY) ;
  uma4 = maxi depert2 avec ( mots UY) ;
si ( neg graph 'n') ; 
 titre ' def init. Avec pertes de precontrainte equi ' 
       uma3 ;
 trac ( de0 et  de1p) ;
 titre ' def init. Avec pertes de precontrainte accro '
        uma4 ;
 trac ( de0 et  de2p) ;
finsi ;
 
*---------- DEFORMATIONS TOTALES   PETITS DEPLACEMENTS   
 
 dept1 = depert1 + dep2equi ;
 dept2 = depert2 + dep2accr ;
  uma5 = mini dept1 avec ( mots UY) ;
  uma6 = mini dept2 avec ( mots UY) ;
   
si ( neg graph 'n') ; 
 titre 'def totale Avec pertes de precontrainte equi ' 
       uma5 ;
 trac ( de0 et  de1p) ;
 titre 'def totale Avec pertes de precontrainte accro ' 
       uma6 ;
 trac ( de0 et  de2p) ;
finsi ; 
 
 
 fin ;

Test precont2 Comments

• The RELA operator

  CL4  = RELA ENSE UX C2 ;
  

  The ENSE option of the RELA operator enables the user to construct the stiffness CL4 (RIGIDITE type) associated with a global motion : the value on the degree of freedom UX (MOT type) is imposed as being identical for all the nodes of C2 (MAILLAGE type).