
Test plas13 Description sheet
Test name
plas13
Calculation type
MECHANICS ELASTIC PLASTIC
Finite element type
POUT
Topic
Material of Ambrois's post type
A post is subjected to a 2-tun load. The material is an Ambrois's post type. It is a global plasticity model for reinforced concrete beams which makes it possible to take into account non linear behavior laws according to the type of loading (axial, bending and shear).
Goal
Study an Ambroy's material with GLOBAL OLARIU elements.
Version
97' customer version
Model description

CASTEM FIGURES
* Test Plas13.dgibi: Jeux de données *
* --------------------------------- *
* *
OPTION ECHO 0;
OPTI DIME 3 ELEM SEG2 MODE TRID;
*******************************************************
* *
* COMPARAISON ETUDE AMBROIS AVEC ELEMENT GLOBAL OLARIU*
* *
*******************************************************
* DEFINITION VALEURS ET ELEMENTS GRAPHIQUES *
*******************************************************
*
* MATERIAU DU TYPE POTEAU AMBROIS
**********************************
*
*POTEAU SOUS 2 T
*******************
*
SIGY = PROG -21.410E6 -25.208E6 -22.904E6
-1.4202E6 0. 1.4202E6 22.904E6 25.208E6 21.410E6 ;
EPSY = PROG -1.80E-2 -8.50E-3 -3.0E-3 -0.40E-4 0.
0.40E-4 3.0E-3 8.50E-3 1.80E-2 ;
*
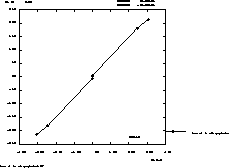
TITRE 'MATERIAU AMBROIS POTEAU SOUS 2 T' ;
EVT = EVOL ROUGE MANU 'EPS' EPSY 'SIG' SIGY ;
;
*******************************************************
* M A I L L A G E 1 *
*******************************************************
*
DENS 1 ;
*
A0 = 0. 0. 0. ;
B0 = 0. 0. 1.50 ;
*
*******************************************************
* DESCRIPTION EN MODELE GLOBAL *
*******************************************************
*
****************
* LES POTEAUX *
****************
*
POT = A0 D 1 B0 ;
*
MOPOTA = MODL POT MECANIQUE ELASTIQUE PLASTIQUE GLOBAL
POUTRE ;
*
*POTEAU PRECONTRAINT SOUS 2 TONNES
**********************************
MOM = PROG -21.401E3 -18.120E3 -0.5961E3 0.
0.5961E3 18.120E3 21.401E3 ;
DPLAS = PROG -3.08E-2 -2.455E-2 -1.764E-4 0.
1.764E-4 2.455E-2 3.08E-2 ;
*
TITRE 'LOI-FLEXION-GLOBAL/2T';
TC=TABLE;
EVE = EVOL BLAN MANU 'DEPLAS' DPLAS 'FLXZ' MOM;
*TC.1 = 'MARQ ETOI';
*DESS EVE CARR LEGE MIMA TC;
*
*MATERIAU DE TYPE GLOBAL
*************************
*
MAPOTA = MATR MOPOTA 'SECT'0.0289
'INRY' 7.137E-5 'INRZ' 7.137E-5
'TORS' 1.178E-4 'SECY' 0. 'SECZ' 0.
'DY' 0.085 'DZ' 0.085
'YOUNG' 35510.E6 'NU' 0.2 'RHO' 2516.
FLXZ EVE 'VECT' ( 0. -1. 0. );
*
*CONDITIONS AUX LIMITES
***********************
*
RIG = RIGI MOPOTA MAPOTA ;
*
BL11 = BLOQ DEPL ROTA ( A0 );
BL12 = BLOQ UX UZ RY RZ ( B0 );
BL1 = BL11 ET BL12 ;
*
RIGV = RIG ET BL1 ;
*
MAS = MASSE MOPOTA MAPOTA ;
MAS1 = MASSE UY 2.0E3 (B0);
MAS= MAS ET MAS1;
*
* CALCUL DES PREMIERS MODES
********************************
*
*PREMOD1 = VIBRE 'PROC' (PROG 0.) RIGV MAS TBAS; PREMOD2 = VIBRE 'SIMULTANE' 0. 2 RIGV2 MASTOT2 TBAS;
*LIST PREMOD1.MODES . 1 ;
*
* INTRODUCTION DU POIDS
*************************
*
V1 = MANU CHPO POT 1 UZ -9.81 'NATURE' 'DIFFUS';
FO1 = MAS * V1 ;
VALTEM1 = PROG 0. 1.E-2 ;
VALPOI = PROG 1. 1. ;
EV1 = EVOL MANU 'TEMPS' VALTEM1 'POIDS' VALPOI ;
CHA1 = CHAR MECA FO1 EV1 ;
*
* INTRODUCTION DE L'ACTION DE CHARGEMENT STATIQUE POUR
******************************************************
* OBTENIR LA LOI DE COMPORTEMENT DE L'ELEMENT GLOBAL
******************************************************
*
V2 = FORCE FY 1. B0 ;
AMPLIF1 = PROG 0. PAS 0.05 0.1;
AMPLIF2 = PROG 0.1 PAS 0.5 1.4266;
AMPLIF = AMPLIF1 ET AMPLIF2;
*
AMPLIF = AMPLIF * 1.E4 ;
Q = DIME AMPLIF ;
VALTEM2 = PROG 1.E-2 PAS 1.E-2 (Q*1.E-2) ;
EV2 = EVOL MANU 'TEMPS' VALTEM2 'CHARGEMENT' AMPLIF ;
CHA2 = CHAR MECA V2 EV2 ;
*
* CALCUL STATIQUE AVEC POIDS UNIQUEMENT
* *************************************
*
TAB = TABLE ;
TAB.'CARACTERISTIQUES' = MAPOTA;
TAB.'MODELE' = MOPOTA;
TAB.'BLOCAGES_MECANIQUES' = BL1;
TAB.'CHARGEMENT' = CHA1;
TAB.'TEMPS_CALCULES' = VALTEM1;
PASAPAS TAB ;
*
* ON ENCHAINE AVEC LE CHARGEMENT
* ******************************
*
VALPOI = PROG Q * 1. ;
EV3 = EVOL MANU 'TEMPS' VALTEM2 'POIDS' VALPOI ;
CHA3 = CHAR MECA FO1 EV3 ;
CHA = CHA3 ET CHA2 ;
*
TAB . 'DYNAMIQUE' = FAUX ;
TAB.FTOL = 1.E-3;
TAB.MTOL = 1.E-3;
TAB.PRECISION = 1.E-5;
TAB . 'MASSE' = MAS ;
TPCAL = 1.E-2 ;
TEMPCAL = PROG 0. PAS TPCAL ((Q-1)*1.E-2);
TAB.'CHARGEMENT' = CHA;
TAB.'TEMPS_CALCULES' = VALTEM2;
PASAPAS TAB ;
*
******************************
* RECUPERATION DES RESULTATS *
******************************
tabd = TAB.DEPLACEMENTS ;
tabc = TAB.CONTRAINTES ;
*
* No DU PAS
************
time = TAB.TEMPS;
ni = (DIME time) - 1;
*
RE = REAC BL1 (tabd.ni);
MOMAX = EXTR RE MX A0;
TEXT 'LE MOMENT MAX ATTEINT EST' MOMAX 'N.m' ;
*
*
PRECIS = 1.E-3;
BOOL1 = (MOMAX <EG ((1 + PRECIS)*21.401E3));
BOOL2 = (((1 - PRECIS)*21.401E3) <EG MOMAX );
BOOL = BOOL1 ET BOOL2;
M1 = CHAINE 'PROBLEME DANS L_ELEMENT GLOBAL';
M2 = CHAINE ' TEST OK';
SI (BOOL EGA FAUX ) ;
MESS M1 ; ERRE 5 ;
SINON;
MESS M2; ERRE 0 ;
FINSI;
*
FIN ;