
Test plas14 Description sheet
Test name
plas14
Calculation type
MECHANICS ELASTIC PLASTIC ACIER_UNI AND BETON_UNI
MECHANICS ELASTIC FIBRE_NL FERAILLE AND FIBRE_NL BETON
Finite element type
QUAS, TRIS
Topic
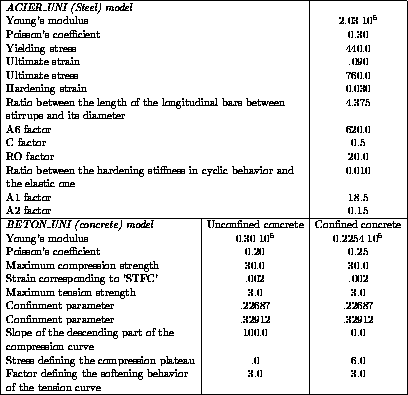
Example of a concrete section with four 20-mm steel bars.
The ACIER_UNI (steel) model is a modified Menegotto-Pinto
uni-axial model, which accounts for the steel buckling.
The BETON_UNI (concrete) model is a Hognestad-like model,
accounting for the confinment.
The geometry of the concrete is as follows:

Version
97' customer version
Model description
Test plas14 Results
CASTEM FIGURES
* Test Plas14.dgibi: Jeux de données *
* --------------------------------- *
* *
graph='N';
saut page;
opti echo 1;
*------------------------------------------------------
*
* EXEMPLE OF A CONCRETE SQUARE SECTION WITH 4 STEEL
* 20mm BARS
* CONCRETE DIMENSIONS: (0.25*0.25)m2 - ALL SECTION
* (0.20*0.20)m2 - CORE SECTION
* TRANSVERSAL REINFORCEMENT: 10mm Bars / 7.0cm
* NOVEMBER 1993
*
*------------------------------------------------------
* Quadrangular Elements
*------------------------------------------
opti dime 2 elem qua4 echo 0 ;
*------------------------------------------
* Triangular Elements
*------------------------------------------
* opti dime 2 elem tri3;
*------------------------------------------
* DEFINITION OF THE STEEL GEOMETRY
*------------------------------------------
ps1 = -9.386d-2 9.386d-2;
ps2 = -9.386d-2 7.614d-2;
ps3 = 1.772d-2 0.0 ;
cars1 = ps1 d 1 ps2 tran 1 ps3;
*
cars2 = cars1 plus ( 17.0e-2 0.0);
cars3 = cars2 plus ( 0.0 -17.0e-2);
cars4 = cars3 plus (-17.0e-2 0.0);
*
meshf = cars1 et cars2 et cars3 et cars4;
meshf = coul meshf bleu;
*------------------------------------------
* DEFINITION OF THE CONCRETE GEOMETRY
*------------------------------------------
* - UNCONFINED
*------------------------------------------
* verd - vertical number of divisions
* hord - horizontal number of divisions
*------------------------------------------
verd = 1;
hord = 8;
*
divu = 2;
*------------------------------------------
pc1 = -12.5d-2 12.5d-2;
pc2 = -12.5d-2 10.0d-2;
pc3 = 2.5d-2 0.0d-2;
carc1 = pc1 d (divu) pc2 tran (divu) pc3;
*
carc2 = carc1 plus ( 22.5d-2 0.0);
carc3 = carc2 plus ( 0.0 -22.5d-2);
carc4 = carc3 plus (-22.5d-2 0.0);
*
pc4 = -10.0d-2 12.5d-2;
pc5 = -10.0d-2 10.0d-2;
pc6 = 20.0d-2 0.0d-2;
carc5 = pc4 d (divu) pc5 tran (verd) pc6;
*
carc6 = carc5 plus ( 0.0 -22.5d-2);
*
pc7 = -12.5d-2 10.0d-2;
pc8 = -10.0d-2 10.0d-2;
pc9 = 0.0d-2 -20.0d-2;
carc7 = pc7 d (divu) pc8 tran (hord) pc9;
*
carc8 = carc7 plus ( 22.5d-2 0.0);
*
meshu = carc1 et carc2 et carc3 et carc4 et
carc5 et carc6 et carc7 et carc8;
meshu = coul meshu jaune;
*------------------------------------------
* - CONFINED
*------------------------------------------
pc10 = -10.0d-2 10.0d-2;
pc11 = 10.0d-2 10.0d-2;
pc12 = 0.0d-2 -20.0d-2;
meshc = pc10 d (verd) pc11 tran (hord) pc12;
meshc = coul meshc rouge;
*
elim (meshf et meshu et meshc) 0.001;
*
titre
'Section:blue=steel,yellow=unconfined concrete
,red=confined concrete';
*
si (ega graph 'Y');
trac (meshf et meshu et meshc);
finsi;
*
opti dime 3;
*
pp0 = 0.0 .0 .0;
pp1 = 1.0 .0 .0;
*
llb = pp0 d 1 pp1;
*
elim (llb et pp0 et pp1) 0.001;
*------------------------------------------
* CARACTERIZATION OF THE STEEL AND CONCRETE MODELS
*------------------------------------------
*------------------------------------------
* Quadrangular Elements
*------------------------------------------
modf = modl meshf mecanique elastique PLASTIQUE
ACIER_UNI quas;
modu = modl meshu mecanique elastique PLASTIQUE
BETON_UNI quas;
modc = modl meshc mecanique elastique PLASTIQUE
BETON_UNI quas;
*------------------------------------------
* Triangular Elements
*------------------------------------------
* modf = modl meshf mecanique elastique fibre_nl
* ferraille tris;
* modu = modl meshu mecanique elastique fibre_nl
* beton tris;
* modc = modl meshc mecanique elastique fibre_nl
* beton tris;
*------------------------------------------
* Steel
*------------------------------------------
matf = matr modf 'YOUN' 2.03e5 'NU' 0.30
'STSY' 440.0 'EPSU' .090 'STSU' 760.0 'EPSH' 0.030
'FALD' 4.375 'A6FA' 620.0 'CFAC' 0.5 'AFAC' 0.008
'ROFA' 20.0 'BFAC' 0.010 'A1FA' 18.5 'A2FA' 0.15;
carf = carb modf 'ALPY' 1. 'ALPZ' 1.;
*------------------------------------------
* Unconfined concrete
*------------------------------------------
matu = matr modu 'YOUN' 0.30e5 'NU' .20
'STFC' 30.0 'EZER' .002 'STFT' 3.0
'ALF1' .22687 'OME1' .32912 'ZETA' 100.0 'ST85' .0
'TRAF' 3.0 'FACL' 1. 'FAMX' 10. 'STPT' .0 'FAM1' 1.
'FAM2' 10.;
caru = carb modu 'ALPY' .66 'ALPZ' .66;
*------------------------------------------
* Confined concrete
*------------------------------------------
* Initial concrete Young modulus =
* 2 * STIFC / ( BETA * EZERO )
*------------------------------------------
matc = matr modc 'YOUN' 0.2254e5 'NU' .25 'STFC' 30.0
'EZER' .002 'STFT' 3.0 'ALF1' .22687 'OME1' .32912
'ZETA' 0.0 'ST85' 6.0 'TRAF' 3.0
'FACL' 1. 'FAMX' 10. 'STPT' .0 'FAM1' 1. 'FAM2' 10.;
carc = carb modc 'ALPY' .66 'ALPZ' .66;
*
modq = modf et modu et modc;
macq = matf et matu et matc et carf et caru et carc;
*------------------------------------------
* USE OF "MOMCUR" PROCEDURE FOR THE ANALYSIS OF THE
* PLASTIC BEHAVIOUR SECCION
*------------------------------------------
* CARACTERIZATION OF THE ACTION
* (CURVATURES ALONG OY AXIS AND CONSTANT AXIAL FORCE)
*------------------------------------------
eppl = 440.0/2.03e5;
*
cy = prog 0 pas .0005 .005 pas .005 .138;
*
ncur = dime cy;
cz = prog ncur * .00;
fa = prog ncur * -.25;
*------------------------------------------
* RESOLUTION
*------------------------------------------
my mz ea = mocu cy cz fa modq macq (1.d-6*eppl);
*------------------------------------------
* OUTPUT DIAGRAMS
*------------------------------------------
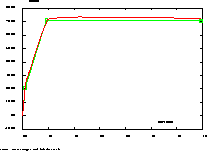
c1= evol rouge manu 'Curvature' cy 'Moment' (my*1.d3);
*------------------------------------------
* TRILINEAR CURVE FOR A TAKEDA MODEL
* FOR THE SAME SECTION
*------------------------------------------
abstak=prog 0. 2.03791E-03 1.85207E-02 1.38834E-01;
ordtak=prog 0. 2.05353E+01 7.10923E+01 7.06633E+01;
albnl=evol vert manu 'Curvature' abstak 'Moment' ordtak;
*------------------------------------------
* PLOT
*------------------------------------------
si (ega graph 'Y');
tt = table;
tt.1 = 'MARQ CARR';
tt.2 = '';
*
titre 'courbe mocu (rouge) et takeda (vert)';
dess (albnl et c1) tt;
*
finsi;
*------------------------------------------
* ERREUR
*------------------------------------------
ordtak=ipol cy abstak ordtak;
errlis=ordtak - (my*1.d3);
errea=((ltl errlis errlis)**0.5) / (dime ordtak);
denom=((ltl ordtak ordtak)**0.5) / (dime ordtak);
errel=errea/denom;
mess 'erreur relative=' errel '(+-=3.5%)';
si (errel > 4.d-2); erre 5;
sinon; erre 0; finsi;
fin;