Bienvenue sur le site Cast3M
Le site Cast3M
Ce site est destiné aux utilisateurs et développeurs du code de calcul de structure et de mécanique des fluide Cast3M. Ils y trouveront de la documentation, les versions "développement" des opérateurs et
procédures ainsi qu'un certain nombre d'outils de travail tels qu'une documentation html
et un moteur de recherche sur l'ensemble des fichiers.
Exemples d'application de Cast3M
| Domaine | Illustration |
|---|---|
Maillages
|
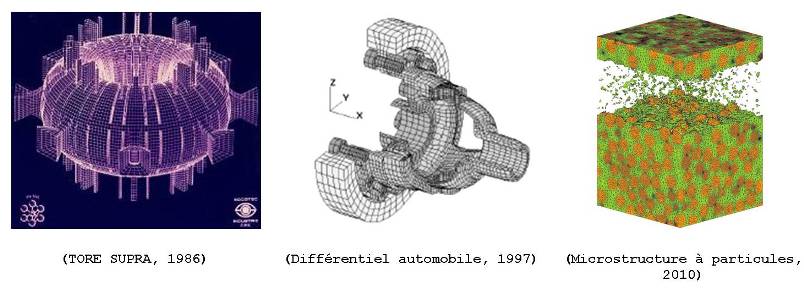
|
|
|
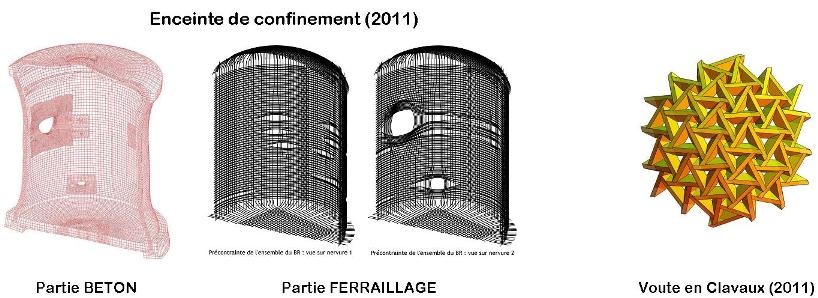
Statique
|
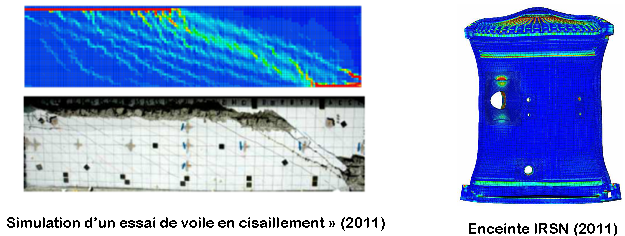
|

|
|
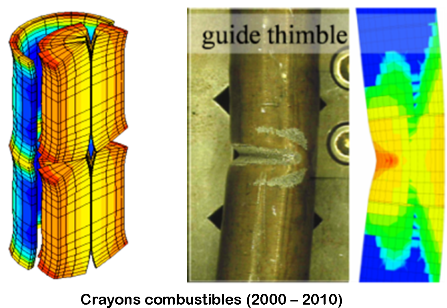
|
|
|
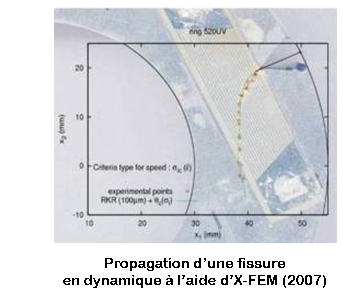
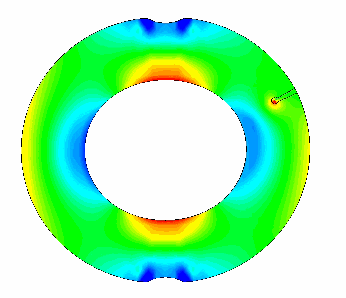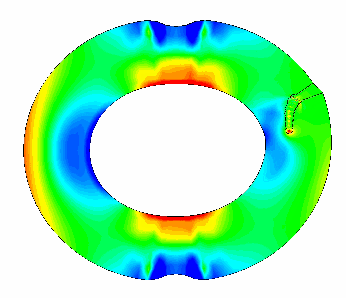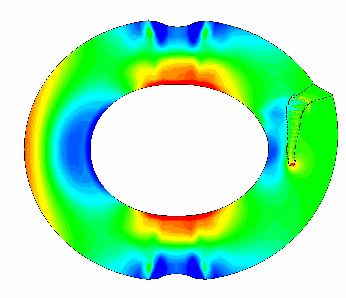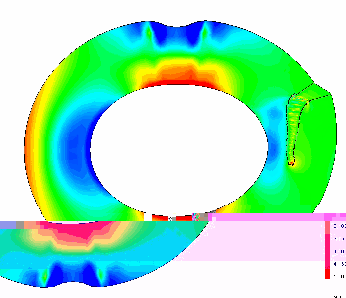
Mécanique de la rupture Animation (*)
|
|
|
Dynamique Animation (*)
|


|
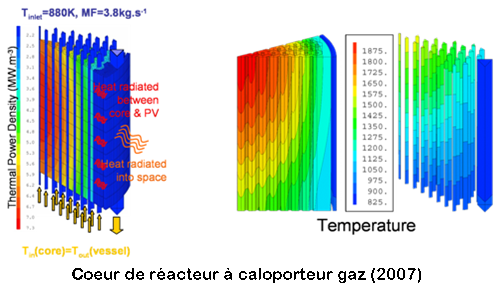
Analyse thermique:
|
|
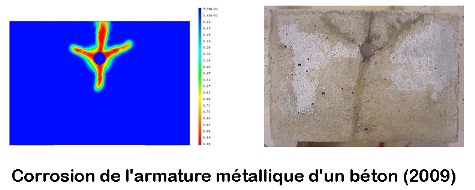
Multi-physiques
|
|
Mécanique des fluides
|

|
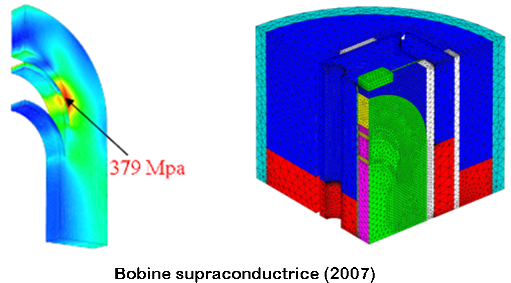
Magnétostatique
|
|
Post-traitement
|
|
Divers
|

|
Présentation de Cast3M
Introduction
Cast3M
est un code de calcul pour l'analyse de structures par la
méthode des éléments finis (E.F) et la modélisation en mécanique des fluides.
A l'origine, ce code a été développé au Service d'études mécaniques et thermiques (SEMT) du Département de modélisation des systèmes et structures (DM2S, anciennement Département de Mécanique et de Technologie, DMT) du Commissariat français à l'Energie Atomique (CEA). Le développement de Cast3M entre dans le cadre d'une activité de recherche dans le domaine de la mécanique, le but étant de définir un instrument de haut niveau, pouvant servir de support valable pour la conception, le dimensionnement et l'analyse de structures et de composants, dans le domaine nucléaire comme dans le secteur industriel classique.
Dans cette optique, Cast3M présente un système complet, intégrant non seulement les fonctions de calcul proprement dites, mais également des fonctions de construction du modèle (pré-processeur) et de traitement des résultats (post-processeur).
Cast3M permet de traiter des problèmes d'élasticité linéaire dans les domaines statique et dynamique (extraction de valeurs propres), des problèmes de thermique, des problèmes non linéaires (comportements, grands déplacements, grandes déformations, contact, frottement...), des problèmes dynamiques « pas-à-pas » selon un schéma implicite, la ruine des structures , problèmes couplant calculs fluides et structuraux, etc.
A l'origine, ce code a été développé au Service d'études mécaniques et thermiques (SEMT) du Département de modélisation des systèmes et structures (DM2S, anciennement Département de Mécanique et de Technologie, DMT) du Commissariat français à l'Energie Atomique (CEA). Le développement de Cast3M entre dans le cadre d'une activité de recherche dans le domaine de la mécanique, le but étant de définir un instrument de haut niveau, pouvant servir de support valable pour la conception, le dimensionnement et l'analyse de structures et de composants, dans le domaine nucléaire comme dans le secteur industriel classique.
Dans cette optique, Cast3M présente un système complet, intégrant non seulement les fonctions de calcul proprement dites, mais également des fonctions de construction du modèle (pré-processeur) et de traitement des résultats (post-processeur).
Cast3M permet de traiter des problèmes d'élasticité linéaire dans les domaines statique et dynamique (extraction de valeurs propres), des problèmes de thermique, des problèmes non linéaires (comportements, grands déplacements, grandes déformations, contact, frottement...), des problèmes dynamiques « pas-à-pas » selon un schéma implicite, la ruine des structures , problèmes couplant calculs fluides et structuraux, etc.
Remarques générales concernant Cast3M
Cast3M, contrairement à de nombreux codes de calcul, ne fonctionne pas en « boîte noire » ;
il donne à l'utilisateur la connaissance du problème effectivement posé et des méthodes employées pour le résoudre.
Cast3M comprend un ensemble de processus élémentaires (bibliothèque d'opérateurs) que l'utilisateur peut enchaîner
pour définir et résoudre ses problèmes. Afin d'illustrer son fonctionnement, on définit parfois Cast3M comme
le « Matlab des éléments finis ».
Cast3M possède un langage de commande constitué d'une série d'opérateurs permettant à l'utilisateur de manipuler les données et les résultats sous forme d'objets en leur donnant des noms : c'est le langage Gibiane. L'utilisateur peut construire un environnement adapté à des applications spécifiques en écrivant des procédures en Gibiane. Le langage Gibiane possède d'ailleurs tous les attributs d'un langage informatique orienté objet : typage dynamique des données, expressions conditionnelles, expressions répétitives, traitement des exceptions, récursivité, possibilité d'écrire des procédures, etc. De plus, aux objets classiquement disponibles dans les langages informatiques usuels (entier, flottant, table.) vient s'ajouter une bibliothèque d'objets propres à la modélisation par éléments finis : maillage, modèle, rigidité. ce qui permet à Gibiane d'être à la fois un langage de programmation et de modélisation.
En pratique, il suffit d'appeler un quelconque opérateur, à l'aide de l'instruction appropriée, pour que ce dernier soit exécuté ; ainsi, l'utilisateur peut définir ou adapter la séquence de résolution à toute sorte de problématique. Le GIBIANE est donc un langage de haut niveau permettant, en particulier, un échange aisé d'informations entre l'utilisateur et le programme. La grande flexibilité offerte par le programme ne dispense toutefois pas l'utilisateur d'apprendre à poser ses problèmes de calcul selon la méthode adoptée dans le code. Il est, par conséquent, important d'analyser et de comprendre comment l'ensemble d'une analyse par éléments finis est structurée et organisée, de façon à pouvoir toujours faire un rapprochement direct entre l'opération mathématique ou logique que vous souhaitez poser et les opérateurs à utiliser.
Cast3M possède un langage de commande constitué d'une série d'opérateurs permettant à l'utilisateur de manipuler les données et les résultats sous forme d'objets en leur donnant des noms : c'est le langage Gibiane. L'utilisateur peut construire un environnement adapté à des applications spécifiques en écrivant des procédures en Gibiane. Le langage Gibiane possède d'ailleurs tous les attributs d'un langage informatique orienté objet : typage dynamique des données, expressions conditionnelles, expressions répétitives, traitement des exceptions, récursivité, possibilité d'écrire des procédures, etc. De plus, aux objets classiquement disponibles dans les langages informatiques usuels (entier, flottant, table.) vient s'ajouter une bibliothèque d'objets propres à la modélisation par éléments finis : maillage, modèle, rigidité. ce qui permet à Gibiane d'être à la fois un langage de programmation et de modélisation.
En pratique, il suffit d'appeler un quelconque opérateur, à l'aide de l'instruction appropriée, pour que ce dernier soit exécuté ; ainsi, l'utilisateur peut définir ou adapter la séquence de résolution à toute sorte de problématique. Le GIBIANE est donc un langage de haut niveau permettant, en particulier, un échange aisé d'informations entre l'utilisateur et le programme. La grande flexibilité offerte par le programme ne dispense toutefois pas l'utilisateur d'apprendre à poser ses problèmes de calcul selon la méthode adoptée dans le code. Il est, par conséquent, important d'analyser et de comprendre comment l'ensemble d'une analyse par éléments finis est structurée et organisée, de façon à pouvoir toujours faire un rapprochement direct entre l'opération mathématique ou logique que vous souhaitez poser et les opérateurs à utiliser.
Organisation du processus de calcul par E.F
Toute analyse générique
effectuée à l'aide de la méthode des éléments finis
peut, en réalité, se scinder en 3 phases successives,
chacune d'entre elles pouvant, à son tour, être
subdivisée en une série de processus élémentaires.
Les phases en question peuvent
être décrites comme suit:
Phase 1. Définition du modèle mathématique
- discrétisation géométrique du domaine étudié ;
- définition des données caractérisant le modèle, parmi lesquelles figurent: le type d'analyse (déformations ou contraintes planes, axisymétrie, etc ...), le type d'éléments (poutres, coques, etc ...), les propriétés du matériau, les caractéristiques géométriques qui ne peuvent être déduites des maillages et des conditions aux limites ;
Phase 2. Résolution du problème discrétisé
- calcul des matrices de rigidité et de masse de chaque élément fini ;
- assemblage des matrices de rigidité et de masse de la structure complète ;
- application des chargements externes ;
- application des conditions aux limites ;
- résolution du système d'équations linéaires d'équilibre.
Phase 3. Analyse et post-traitement des résultats
Les résultats peuvent
être, soit des quantités locales comme les
déplacements, les contraintes, les déformations, soit
des quantités globales, telles que l'energie de
déformation ou encore la déformation maximale.
Les programmes de calcul classiques sont rigoureusement structurés selon cette logique, chaque phase étant associée à un module déterminé du code :
Les programmes de calcul classiques sont rigoureusement structurés selon cette logique, chaque phase étant associée à un module déterminé du code :
- un pré-processeur pour la définition du modèle complet , qui transmet les données au programme de calcul proprement dit , dès que ces dernières sont élaborées ;
- le programme de calcul qui, dès que la sélection d'une procédure de résolution est donnée, envoie une série de processus que l'utilisateur est contraint d'utiliser en « boite noire » ;
- un post-processeur qui, dès qu'il a recu les résultats de ces processus , procède aux traitements nécessaires.
-
Il apparaît toutefois
clairement qu'une structure de ce type exclut toute
intervention, de la part de l'utilisateur, dans l'une
quelconque de ces phases et ce, dans l'intention
d'apporter des modifications répondant à ses propres
besoins. Pourtant, une grande souplesse d'utilisation
peut s'avérer très utile lorsque les problèmes que
l'utilisateur se propose de résoudre sont variés et
localisés en différents points du processus de
résolution.
-
Ainsi, l'utilisateur
pourra se heurter à de grandes difficultés lorsqu'il
s'agira de modéliser de la facon la plus adaptée aux
nécessités de l'analyse, la géométrie de la
structure, généralement constituée de plusieurs
parties très complexes.
-
En outre, la
discrétisation exige de distribuer les éléments d'une
certaine facon : afin de rentabiliser au mieux les coûts
de l'analyse, il convient en effet de densifier les
éléments dans les zones les plus particulièrement
exposées à de brusques variations de la fonction
inconnue et, au contraire, de les raréfier dans les
zones n'offrant que peu d'intéret.
-
Il peut également
s'avérer extrêmement difficile de rassembler,
c'est-à-dire de rendre compatibles entre elles, au sein
d'une même structure, plusieurs formulations
mathématiques différentes (poutres, coques, solides,
...) se rapportant à diverses parties de la même
structure, ou, encore, de définir des types particuliers
de conditions aux limites ou de chargement.
-
Dans le cadre d'une
analyse, il peut, par conséquent, s'avérer très
intéressant de pouvoir définir pas à pas la séquence
la plus adaptée des processus élémentaires présents
dans les différentes phases en les concaténant et en
fournissant, à chaque fois, les données requises.
Particularités de Cast3M :
Cast3M est un système
conçu et développé dans l'optique de dépasser les
limites d'adaptabilité offertes par les codes
conventionnels.
Ainsi,
l'utilisateur dispose notamment d'un macrolangage,
GIBIANE, qui lui permet de définir aisément chacune des
opérations des diverses phases d'une analyse, à l'aide
d'instructions extrêmement simples.
Par exemple, le calcul des
contraintes dans une structure à partir des
déplacements peut être effectué, soit directement à
l'aide d'une seule instruction, si l'on connait les
caractéristiques géométriques et celles du matériau
ou les déplacements, soit à l'aide de plusieurs
instructions successives permettant de calculer, en
premier lieu, le vecteur des déformations e=Bu, puis la
matrice d'élasticité D et enfin le produit s=De.
Ces opérations sont
effectuées sur des objets qui, le cas échéant,
représenteront la structure complète à étudier ou
chacune de ses composantes élémentaires.
Tout cela est possible
grâce à la création, dans le programme, d'un système
original de gestion des données et des informations. Les
données du problème, qu'il s'agisse des propriétés
mécaniques du matériau, des caractéristiques
géométriques, du maillage créé, des champs de forces,
des contraintes... peuvent, par conséquent, être
manipulées facilement en se référant aux noms choisis
et attribués directement par l'utilisateur.
Une information ou un
groupe d'informations constitue ce qui est défini comme
un « OBJET » dans le programme.
Outre le fait qu'ils sont
nommés par l'utilisateur, ce qui lui permet de les
retrouver, tous les objets sont typés ce qui permet de
retrouver la structure des données associées. Il peut
s'agir d'objets de type ENTIER ou REEL, caractérisés
par une structure très simple ; d'autres, au contraire,
seront plus complexes, comme ceux de type MMODEL par
exemple, qui contiennent la référence à la géométrie
de la structure, la formulation des éléments finis
relatifs, ou encore le comportement du matériau.
Il est clair que pour
l'utilisateur le nom représente la caractéristique la
plus importante; le type est avant tout une nécessité
informatique, permettant toutefois de procéder à des
vérifications syntaxiques utiles des données.
Unités de mesure: Cast3M ne dispose d'aucun système particulier d'unités de mesure: c'est à l'utilisateur de fournir, dans la phase de définition du modèle, les données à intégrer dans un système présentant les dimensions adaptées. La cohérence de ce système pourra être vérifiée en appliquant la loi fondamentale de la dynamique selon laquelle: F=mg. Une fois que les unités de mesure utilisées dans les données sont définies, tous les résultats seront exprimés dans ces mêmes unités. Il existe cependant une exception à cette règle, à savoir la mesure des angles qui doit toujours être exprimée en degrés. En revanche, les valeurs de température et le coefficient de dilatation thermique doivent être exprimés dans des unités cohérentes.
Unités de mesure: Cast3M ne dispose d'aucun système particulier d'unités de mesure: c'est à l'utilisateur de fournir, dans la phase de définition du modèle, les données à intégrer dans un système présentant les dimensions adaptées. La cohérence de ce système pourra être vérifiée en appliquant la loi fondamentale de la dynamique selon laquelle: F=mg. Une fois que les unités de mesure utilisées dans les données sont définies, tous les résultats seront exprimés dans ces mêmes unités. Il existe cependant une exception à cette règle, à savoir la mesure des angles qui doit toujours être exprimée en degrés. En revanche, les valeurs de température et le coefficient de dilatation thermique doivent être exprimés dans des unités cohérentes.
Le langage de Cast3M: GIBIANE
GIBIANE est un langage de
haut niveau permettant à l'utilisateur de communiquer
directement avec le programme par un échange de
données. Toutes les opérations exécutées avec GIBIANE
consistent en une manipulation des objets existants,
dans le but de les modifier ou d'en créer de nouveaux.
La syntaxe d'une opération
élémentaire peut faire intervenir plusieurs objets et
se présente sous différentes formes, selon que le
résultat obtenu consiste en une modification d'un ou de
plusieurs objets existants ou en la création d'un ou de
plusieurs nouveaux objets. Dans le premier cas,
l'instruction est du type :
Dans le second cas, l'instruction est du type:
Les opérations sont exécutées par des opérateurs agissant directement sur des objets fournis en argument. Les opérandes peuvent être des objets déjà disponibles, contenant des informations caractéristiques de l'analyse à effectuer, ou des objets spécifiques définis à seule fin de permettre l'exécution de l'opération requise. Ainsi, le simple fait de donner un nom à un nombre entier ou réel (PAR = 12, PI = 3.14) permet de générer les objets correspondants de type ENTIER et FLOTTANT, pouvant alors être utilisés pour effectuer des opérations algébriques avec d'autres objets (multiplication, division, etc.). Les opérations exécutées sur les objets conduisent à la création de nouveaux objets pouvant être du même type que les opérandes ou de type différent. Ainsi, les opérateurs de type algébrique tels que : +, -, *, /, par exemple, ou l'opérateur ET, qui unit deux ou plusieurs objets, sont généralement utilisés pour créer de nouveaux objets, de même type que les objets d'origine. En revanche, des opérateurs plus sophistiqués créent des objets de type différent. Un exemple: l'opérateur MODL utilise un objet de type MAILLAGE et des objets de type MOT pour créer un nouvel objet de type MMODEL contenant les références à la géométrie, à la formulation élément fini, au comportement du matériau de la structure analysée.
- DIRECTIVES OPERANDES ;
Dans le second cas, l'instruction est du type:
- RESULTATS = OPERATEUR OPERANDES ;
Les opérations sont exécutées par des opérateurs agissant directement sur des objets fournis en argument. Les opérandes peuvent être des objets déjà disponibles, contenant des informations caractéristiques de l'analyse à effectuer, ou des objets spécifiques définis à seule fin de permettre l'exécution de l'opération requise. Ainsi, le simple fait de donner un nom à un nombre entier ou réel (PAR = 12, PI = 3.14) permet de générer les objets correspondants de type ENTIER et FLOTTANT, pouvant alors être utilisés pour effectuer des opérations algébriques avec d'autres objets (multiplication, division, etc.). Les opérations exécutées sur les objets conduisent à la création de nouveaux objets pouvant être du même type que les opérandes ou de type différent. Ainsi, les opérateurs de type algébrique tels que : +, -, *, /, par exemple, ou l'opérateur ET, qui unit deux ou plusieurs objets, sont généralement utilisés pour créer de nouveaux objets, de même type que les objets d'origine. En revanche, des opérateurs plus sophistiqués créent des objets de type différent. Un exemple: l'opérateur MODL utilise un objet de type MAILLAGE et des objets de type MOT pour créer un nouvel objet de type MMODEL contenant les références à la géométrie, à la formulation élément fini, au comportement du matériau de la structure analysée.
Possibilités offertes par Cast3M
Notion de procédures:
La
structure adoptée dans Cast3M offre, avant toute
chose, la possibilité d'élaborer des procédures qui
sont, en quelque sorte, des opérateurs de niveau
supérieur, appelant à leur tour des opérateurs
élémentaires.
Ces procédures sont
créées pour répondre à des besoins divers:
Développement de nouveaux opérateurs: La structure particulière de Cast3M permet non seulement d'élaborer des procédures propres à résoudre de nouveaux types de problème, mais, également, de définir, dans des cas exceptionnels, des opérateurs différents de ceux existants. Les nouveaux opérateurs peuvent, en réalité, être développés, mis au point et vérifiés indépendamment des autres. Pour cela, il suffit de connaitre la structure des données contenues dans les objets traités par le nouvel opérateur et dans les objets communs à tout le programme. Cette possibilité s'avère particulièrement utile lorsque l'analyse exige des adaptations spécifiques. Naturellement, la création de nouveaux opérateurs suppose, de la part du développeur, une connaissance approfondie du langage de programmation qui porte le nom d'ESOPE et qui constitue une sorte de langage FORTRAN de niveau supérieur. Sans entrer dans les détails, il suffit de préciser qu'une entité informatique telle qu'un sous-programme est écrite en ESOPE, traduite en norme FORTRAN, puis compilée de manière classique. Pour lever toute ambiguïté, il convient de bien distinguer :
- En premier lieu, il est possible d'utiliser les mêmes données pour plusieurs opérateurs, ce qui permet de les regrouper facilement et de les retrouver à l'aide d'une seule instruction.
- En second lieu, dans le cas de problèmes assez complexes ou répétitifs, il peut être gênant pour l'utilisateur d'avoir à définir chaque fois explicitement des opérations très standardisées.
- Enfin, pour des utilisations par des personnes peu familiarisées avec la méthode des éléments finis, il est bon de pouvoir revenir à un fonctionnement en « boite noire » du programme. Ceci revient à masquer tout le détail des opérations élémentaires par une seule procédure.
- Elles peuvent être utilisées comme les opérateurs élémentaires.
- Une procédure peut en appeler d'autres et peut s'appeler elle-même.
- Une procédure peut être constituée d'autres procédures.
- La séquence d'opérateurs élémentaires contenue dans une procédure est toujours visible.
Développement de nouveaux opérateurs: La structure particulière de Cast3M permet non seulement d'élaborer des procédures propres à résoudre de nouveaux types de problème, mais, également, de définir, dans des cas exceptionnels, des opérateurs différents de ceux existants. Les nouveaux opérateurs peuvent, en réalité, être développés, mis au point et vérifiés indépendamment des autres. Pour cela, il suffit de connaitre la structure des données contenues dans les objets traités par le nouvel opérateur et dans les objets communs à tout le programme. Cette possibilité s'avère particulièrement utile lorsque l'analyse exige des adaptations spécifiques. Naturellement, la création de nouveaux opérateurs suppose, de la part du développeur, une connaissance approfondie du langage de programmation qui porte le nom d'ESOPE et qui constitue une sorte de langage FORTRAN de niveau supérieur. Sans entrer dans les détails, il suffit de préciser qu'une entité informatique telle qu'un sous-programme est écrite en ESOPE, traduite en norme FORTRAN, puis compilée de manière classique. Pour lever toute ambiguïté, il convient de bien distinguer :
- Le langage du développeur: ESOPE
- Le langage de l'utilisateur: GIBIANE
Présentation et utilisation de Cast3M
Un document de présentation générale de Cast3M, qui retrace, en première partie, les considérations qui ont guidées sa conception .
Lire le document complet (html).
Lire le document complet (html).
© Cast3M 2003 - Tous droits réservés.
Mentions légales

