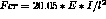Test dyna_nl3 Description sheet

Test name

Calculation type

Finite element type

Topic

Follower pressure and wavering of a beam.

The response of a released beam is studied with an axial compression force which is a little higher than the theoretical value of wavering force ().
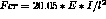The beam is clamped-free. The follower force is described by an equivalent pressure which is applied on a small shell located on the end of the beam.
The system is disturbed by a small transversal displacement which is imposed at the free end.

Goal

Version

Model description

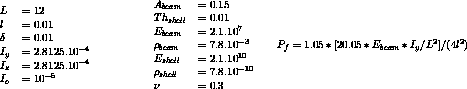
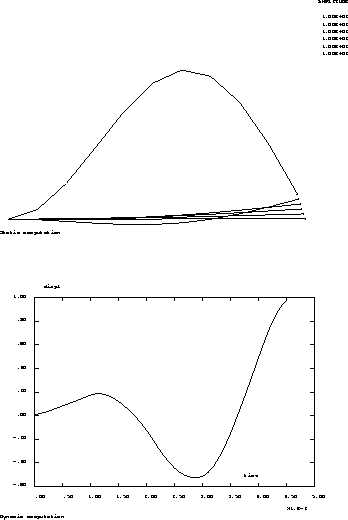
Test dyna_nl3 Results

Results

Maximum amplitude (point bb) : 0.97959
Margin : 0.04%

CASTEM figures

*         Test Dyna_nl3.dgibi: Jeux de données        *
*         ------------------------------------        *
*                                                     *
complet = vrai;
*
*************************************************
*  pour calcul complet mettre complet à : vrai;
***************************************************
*======================================================
*       TEST DES LA PRESSION SUIVEUSE EN DYNAMIQUE
*
*       FLOTTEMENT D'UNE POUTRE ENCASTREE-LIBRE
*
* On etudie la reponse de la poutre à un lacher quand 
* elle est soumise à une force de compression axiale
* legerement superieure à la valeur theorique de la 
* force critique de flottement (Fcr = 20.05*E*I/l**2)
* On doit obtenir une reponse d'amplitude croissante.
*
*******************************************************
*                                                    ==   
*    /|aa___________________bb                       ==
*    /|______________________|<----- F               ==
*    /|                        cc                    ==
*           EQUIVALENT A     /|                      ==  
*                        dd / |                      ==  
*    /|aa_________________bb|<--                     ==
*    /|_____________________|<--  PRESSION           ==
*    /|                     |<--                     ==
*                        ee |/ ff                    ==
*                                                    ==
*                                                    ==
*====================================================== 
graph = faux;
option dime 3 elem seg2 tri3 ;
*======================================================
* definition de la geometrie
* la force suiveuse est modelisee par une pression équi
* valente appliquée sur une petite plaque fixée à l'ex
* trémité de la poutre
*======================================================
aa = 0 0 0 ;
bb = 12 0 0;
cc = 12 0.01 0.01 ;
dd = 12 0.01 -0.01 ;
ee = 12 -0.01 -0.01 ;
ff = 12 -0.01 0.01 ;
dens1 = 10 ;
lig1 = aa d dens1 bb ;
lig2 = cc d 2 dd d 2 ee d 2 ff d 2 cc ;
surf1 = surf plan lig2 ;
geo = lig1 et surf1 ;
elim 1.e-4 geo ;
*=====================================================
*definition des conditions aux limites
* encastrement à la base de la poutre et mouvement 
* dans le plan xOy
*=====================================================
cl1 = bloq rota depla aa ;
cl2 = bloq uz rx ry surf1 ;
cl3 = bloq bb uy ;
*======================================================
*      definition du modele, du materiau et 
*               des caracteristiques
*======================================================
mo1 = mode lig1 mecanique pout ;
mo2 = mode surf1 mecanique coq3 ;
ma1 = mate mo1 youn 2.1e7 nu 0.3 rho 7.8e-3 ;
ma2 = mate mo2 youn 2.1e10 nu 0.3 rho 7.8e-10 ;
ca1 = cara mo1 sect 0.15 inry 2.8125e-4 inrz 2.8125e-4
                                            tors 1.e-5;
ca2 = cara mo2 epai 0.01 ;
mat1 = ma1 et ca1 ;
mat2 = ma2 et ca2 ;
mattotal = mat1 et mat2 ;
mototal = mo1 et mo2 ;
*======================================================
* calcul des matrices de rigidite et de masse
*======================================================
ri1 = rigi mototal mattotal ;
ritotal = ri1 et cl1 et cl2 ;
masst = masse mototal mattotal ;
*======================================================
* chargement par pression equivalente a la force 
* critique de flottement pondérée par un coefficient 
* de 1.05 pour se placer legerement au dessus de 
* l'instabilité.
*
* on impose un petit deplacement transverse pour 
* perturber le systeme.
*======================================================
fo2 = depi cl3 .01 ;
fo0 = manu chpo geo 1 p (2050781.25*1.05) 
      nature discret ;
*======================================================
*               calcul non lineaire
* calcul statique sous la force de compression et la
* force transversale de perturbation
*======================================================
dt = 0.00001 ;
li1 = prog  0. dt ;
li2 = prog  0. 1 ;
ev = evol manu t (li1 ) f(t) (li2 )  ;
fcons = char dimp  fo2 ev ;
fncons = char psui fo0 ev ;
fco = fncons et fcons ;
lis1a = prog 0. pas (dt/5) dt ;


tab3 = table ;
tab3.grands_deplacements = vrai ;
tab3.chargement = fco ;
tab3.blocages_mecaniques = cl1  et cl2 et cl3 ;
tab3.modele =  mototal ;
tab3.caracteristiques = mattotal ;
tab3.temps_calcules =  lis1a ;
tab3.precision      =  1e-8  ;
tab3.deltaiter = 20 ;

pasapas tab3 ;

oeil = 0 0 10000 ;
dim1 = dime (tab3.deplacements) ;
lisx = prog  ; lisy = prog ;
 repeter bou1 dim1 ;
   n = &bou1 - 1 ;
   uy1 = extr tab3.deplacements.n 'UY' bb ;
   lisy = lisy et (prog uy1) ;
   lisx = lisx et (prog tab3.temps. n);
   def1 = defo tab3.deplacements.n  geo 100 ;
     si (&bou1 ega 1) ; deft = def1 ; sinon ;
     deft = deft et def1 ; finsi ;
 fin bou1 ;
ev1 = evol manu 'temps' lisx 'depl' lisy ;
si graph ; trac deft oeil cach anime ; finsi ;


*======================================================
*           calcul non lineaire dynamique
*======================================================
* definition de l'évolution du chargement 
* durée de la phase de chargement statique :dt

ev2 = evol manu (prog dt 100) (prog 1 1 ) ;
*
fncons = char psui fo0 ev2 ;
si complet;
lis1c = prog dt pas .001 .045 ;
sinon;
lis1c = prog dt  pas .001 0.005;
finsi;
tab3.chargement = fncons ;
tab3.blocages_mecaniques = cl1  et cl2 ;
tab3.dynamique = vrai ;
tab3.temps_calcules = lis1c ;

pasapas tab3 ;

*====================================================
* exploitation des resultats : deplacement de l'
* extrémité de la poutre (point bb)
*====================================================

dim1 = dime (tab3.deplacements) ;
lisx = prog  ; lisy = prog ;
 repeter bou1 dim1 ;
   n = &bou1 - 1 ;
   uy1 = extr tab3.deplacements.n 'UY' bb ;
   lisy = lisy et (prog uy1) ;
   lisx = lisx et (prog tab3.temps. n);
 fin bou1 ;
ev1 = evol manu 'temps' lisx 'depl' lisy ; 
list lisy;
 si graph ; dess ev1  ; finsi ;

* la reference pour le test est le resultat d'une 
*             certaine version de C2000
dmax = maxi abs lisy ; list dmax ;
si complet ;
valtes = 1.1;
sinon;
valtes =  .082;
finsi;
err1 = abs ((dmax - valtes)/valtes);
list err1 ;
 si (err1 > .05) ; erreur 5 ;
 sinon ; erre 0 ; finsi ;  
fin ;

Test dyna_nl3 Comments

1. First step : Static computation under the compression force and the disturbing transversal force

   fo2 = depi cl3 .01 ;
   fo0 = manu chpo geo 1 p (2050781.25*1.05) nature discret ;
   **
   dt = 0.00001 ;
   li1 = prog 0. dt ;
   li2 = prog 0. 1 ;
   ev = evol manu t (li1 ) f(t) (li2 ) ;
   fcons = char dimp fo2 ev ;
   fncons = char psui fo0 ev ;
   fco = fncons et fcons ;
   lis1a = prog 0. pas (dt/5) dt ;
   **
   tab3 = table ;
   tab3.grands_deplacements = vrai ;
   tab3.chargement = fco ;
   tab3.blocages_mecaniques = cl1 et cl2 et cl3 ;
   tab3.modele = mototal ;
   tab3.caracteristiques = mattotal ;
   tab3.temps_calcules = lis1a ;
   pasapas tab3 ;
   

   In the static computation the free tip of the beam has an imposed vertical displacement (fo2). The follower pressure is described with the fo0 object. The loads are defined as a function of time with CHAR operator and the evolution ev.
   The PASAPAS subroutine is called by using 6 computation steps (defined with lis1a).

2. Second step : Dynamic computation under the compression force and the release of the beam

   ev2 = evol manu (prog dt 100) (prog 1 1 ) ;
   **
   fncons = char psui fo0 ev2 ;
   si complet;
   lis1c = prog dt pas .001 .045 ;
   sinon;
   lis1c = prog dt pas .001 0.005;
   finsi;
   tab3.chargement = fncons ;
   tab3.blocages_mecaniques = cl1 et cl2 ;
   tab3.dynamique = vrai ;
   tab3.temps_calcules = lis1c ;
   **
   pasapas tab3 ;
   

   The beam is released : the boundary condition cl3 and imposed displacement fo2 are removed. The applied load is the follower pressure defined as a function of time (fncons).
   The computation is a dynamic analysis so tab3.dynamique is true.