Test name
dyna_nl1
Calculation type
MECHANICS 2D
NON LINEAR GEOMETRICAL DYNAMICS
Finite element type
BARR
Topic
Free oscillations of an oscillator of Duffing type.
The bar is clamped at one end and prestressed. On the free end is imposed a vertical displacement. Then the bar is released and has free oscillations.
Goal
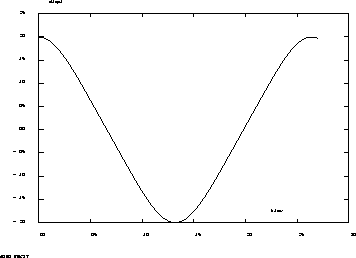
Find the amplitude and period of the free oscillations of the bar.
Version
97' customer version
Model description
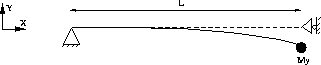
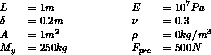
Test dyna_nl1 Results
Results
Margin in amplitude : 0.007%
Margin in period :0.3%
CASTEM figures
* Test Dyna_nl1.dgibi: Jeux de données *
* ------------------------------------ *
* *
complet = vrai;
*
*************************************************
* pour calcul complet mettre complet à : vrai;
*************************************************
*******************************************************
*
* dynamique non lineaire geometrique
*
* oscillations libres d'un oscillateur de type Duffing
*
* reference :J. ARGYRIS H.P. MLEJNEK
* DYNAMICS OF STRUCTURES (p. 494)
*
*******************************************************
opti echo 0 ;
graph = faux ;
OPTI DIME 2 ELEM SEG2 MODE PLAN CONT ; ;
P1 = 0. 0. ; P2 = 1. 0. ;
ST = P1 D 1 P2 ;
MO = MODE ST MECANIQUE BARR ;
MA1 = MATE MO YOUN 1E7 NU 0.3 RHO 0.;
CAR1 = CARA MO SECT 1. ;
MACA= MA1 ET CAR1;
MASS1 = MASS UY 250. P2 ;
CL1 = BLOQ UX uy P1 ;
CL2 = BLOQ UX P2 ;
CL3 = BLOQ UY P2 ;
CL = CL1 ET CL2 ;
* precontrainte de 500 N
RI1 = RIGI MACA MO ;
f1 = force fx 500 p2 ;
dep1 = reso (ri1 et cl1 et cl3) f1 ;
sig1 = sigm dep1 mo maca ;
*sig1 = manu 'CHML' mo 'EFFX' 500. 'TYPE' 'CONTRAIN'
* 'STRESSES' ;
* deplacement impose en statique
t1 = 1e-10 ;
FP11 = DEPI CL3 .2;
LIX1 = PROG 0. t1 100 ;
LIY1 = PROG 0. 1 1 ;
EV1 = EVOL MANU T LIX1 F(T) LIY1 ;
CHA1 = CHAR MECA FP11 EV1 ;
tab2 = table ;
tab2.grandes_rotations = vrai ;
TAB2.'BLOCAGES_MECANIQUES' = CL et cl3 ;
TAB2.'MODELE' = MO;
Tab2.'K_SIGMA' = VRAI ;
TAB2.'CARACTERISTIQUES' = MACA;
TAB2.'CHARGEMENT' = CHA1;
TAB2.'CONTRAINTES' = TABLE;
TAB2.'CONTRAINTES' . 0 = SIG1 ;
LIS11 = PROG 0. (.33*t1) (.66*t1) t1 ;
TAB2.'TEMPS_CALCULES' = LIS11;
PASAPAS TAB2 ;
* lacher et oscillations libres en dynamique
si complet;
t2 = .27 ;
sinon;
t2 = .02;
finsi;
dt = .002 ;
f1 = force fy 0. p2 ;
cha2 = char meca f1 ev1 ;
tab2.dynamique = vrai ;
tab2.masse_constante = mass1 ;
tab2.ftol = 1e-4 ;
TAB2.'BLOCAGES_MECANIQUES' = CL ;
LIS22 = PROG (t1 + dt) pas dt (t1 + t2) ;
TAB2.'TEMPS_CALCULES' = LIS22;
TAB2.'CHARGEMENT' = CHA2;
PASAPAS TAB2 ;
NDIM = (DIME ( TAB2 . DEPLACEMENTS )) ;
PGY = PROG ;
REPETER TBOU2 NDIM;
LEDEP = TAB2 . DEPLACEMENTS. (&TBOU2 - 1);
V = EXTR LEDEP UY P2 ;
PGY = PGY ET ( PROG V ) ;
FIN TBOU2 ;
ev1 = evol manu 'temps' (lis11 et lis22) 'depl' pgy ;
si graph ;
dess ev1 ;
finsi ;
*recherche de l'amplitude et de la periode
si complet;
dim1 = enti ((t2 - .25)/dt) ;
maxuy = 0 ;
tt = .25 ;
repeter bou1 dim1 ;
tt = tt + dt ;
uy1 = ipol tt (lis11 et lis22) pgy ;
si (uy1 > maxuy) ;
maxuy = uy1 ;
tp = tt ;
finsi ;
fin bou1 ;
valres = .2;
sinon;
tp =.2648;
valres = .171 ;maxuy = pgy extr ( dime pgy);
finsi;
** periode theorique .264791269s
** amplitude theorique .2 ;
err1 = abs ((maxuy - valres)/valres * 100) ;
err2 = abs ((tp - .2648)/.2648 *100) ;
mess 'erreur en amplitude'err1'%';
mess 'erreur en periode'err2'%' ;
si ((err1 > .1) ou (err2 > .5));
erre 5 ;
sinon ;
erre 0 ;
finsi ;
fin ;
Test dyna_nl1 Comments
RI1 = RIGI MACA MO ;
f1 = force fx 500 p2 ;
dep1 = reso (ri1 et cl1 et cl3) f1 ;
sig1 = sigm dep1 mo maca ;
A horizontal force of 500 N is applied on the free end of the bar. To get a prestress we compute the stresses related to this load. Those results will be added in the following step.
FP11 = DEPI CL3 .2 ;
LIX1 = PROG 0. t1 100 ;
LIY1 = PROG 0. 1 1 ;
EV1 = EVOL MANU T LIX1 F(T) LIY1 ;
CHA1 = CHAR MECA FP11 EV1 ;
The operator DEPI imposes a specific value for the degree of freedom described in CL3. It means that UY-displacement of point P2 (related to CL3) will be equal to 0.2 m. The object created by DEPI is of CHPOINT type and must be added to the second member of the equation. To perform a dynamic computation the second member must be a function of time : the operator CHAR is then used to multiply the second member by a factor which is defined as a function of time (EV1).
tab2 = table ;
tab2.grandes_rotations = vrai ;
TAB2.'BLOCAGES_MECANIQUES' = CL et cl3 ;
TAB2.'MODELE' = MO;
Tab2.'K_SIGMA' = VRAI ;
TAB2.'CARACTERISTIQUES' = MACA;
TAB2.'CHARGEMENT' = CHA1;
TAB2.'CONTRAINTES' = TABLE;
TAB2.'CONTRAINTES' . 0 = SIG1 ;
LIS11 = PROG 0. (.33*t1) (.66*t1) t1 ;
TAB2.'TEMPS_CALCULES' = LIS11;
PASAPAS TAB2 ;
The non linear problem is solved by using PASAPAS subroutine. The single object necessary for the computation is a table (TAB2). The user must create this table which has indexes defined by keywords :
- TAB2.grandes_rotations : boolean equal to VRAI if the second-order terms must be taken into account for the strain tensor (in the case of large rotations or large deformations)
- TAB2.BLOCAGES_MECANIQUES : contains the boundary conditions
- TAB2.MODELE : contains the model object
- TAB2.K_SIGMA : boolean equal to VRAI if the matrix K_SIGMA is to be added to the iteration operator
- TAB2.CARACTERISTIQUES : contains material and geometrical caracteristics
- TAB2.CHARGEMENT : contains the load object (defined as a function of time)
- TAB2.CONTRAINTES : is a table : TAB2.'CONTRAINTES'.0 contains the stresses at the beginning of first step. The given values are the previous computed prestresses.
- TAB2.TEMPS_CALCULES : the given list of reals defines the values of time for which results are requested.
The subroutine is called by the following instruction : PASAPAS TAB2 .
t2 = .27 ;
dt = .002 ;
f1 = force fy 0. p2 ;
cha2 = char meca f1 ev1 ;
tab2.dynamique = vrai ;
tab2.masse_constante = mass1 ;
tab2.ftol = 1e-4 ;
TAB2.'BLOCAGES_MECANIQUES' = CL ;
LIS22 = PROG (t1 + dt) pas dt (t1 + t2) ;
TAB2.'TEMPS_CALCULES' = LIS22;
TAB2.'CHARGEMENT' = CHA2;
PASAPAS TAB2 ;
The free oscillations are simulated by a zero force.
TAB2.dynamique is a boolean. If its value is true, it means that it is a dynamic analysis.
TAB2.masse_constante defines a constant lumped mass matrix (mass1).
TAB2.ftol indicates that the effort equilibrium will be checked up to about 1e-4.
NDIM = (DIME ( TAB2 . DEPLACEMENTS )) ;
PGY = PROG ;
REPETER TBOU2 NDIM;
LEDEP = TAB2 . DEPLACEMENTS. (&TBOU2 - 1);
V = EXTR LEDEP UY P2 ;
PGY = PGY ET ( PROG V ) ;
FIN TBOU2 ;
ev1 = evol manu 'time' (lis11 et lis22) 'displ' pgy ;
dess ev1 ;
The results of PASAPAS subroutine are stored in TAB2 table : TAB2.DEPLACEMENTS is a table which has as many indexes as the number of requested saving times.
TAB2.DEPLACEMENTS.i contains the displacements computed for the ith step.