Test name
dy_devo6
Calculation type
MECHANICS DYNAMICS 3D
IMPACT, LINKAGE POINT-PLANE
Topic
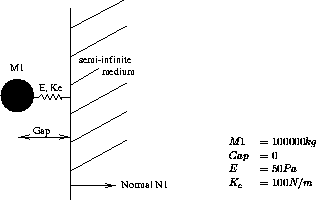
Impact of a great mass against a plane.
A great mass with a sinusoidal movement (composed by two different amplitudes) impacts a plane.
The computation is done with a linkage point-plane and with taking into consideration the plastification of the impact spring.
The computation restart is also checked.
Goal
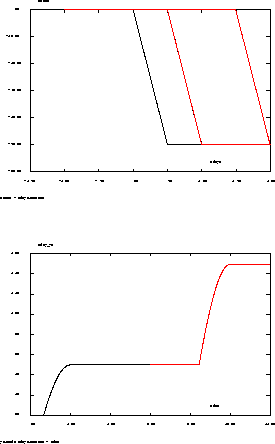
Get the evolution of the impact force according to the displacement and get the evolution of the plastic displacement according to the time.
Reference
Version
97' customer version
Model description

Test dy_devo6 Results
Results
Maxima of plastic displacements :

CASTEM figures
* Test Dy_devo6.dgibi: Jeux de données *
* ------------------------------------ *
* *
*******************************************************
*
* DYNE LIAISON POIN_PLAN
* avec plastification du ressort de choc
*
* il s'agit d'une grande masse animée d'un mouvement
* sinusoidale (avec deux amplitudes differentes) qui
* impacte un plan
*
* on teste aussi la reprise de calcul
*
*******************************************************
opti echo 0 ;
graph ='N' ;
*******************************************************
m1 = 100000 ; comm 'masse impactée';
ke = 100. ; comm 'raideur de choc';
se1 = 50. ; comm 'limite élastique';
dt = .01 ; comm 'pas de temps';
t1 = 12 ; comm 'durée du calcul';
*******************************************************
opti dime 3 ;
pp1 = 0 0 0 ;
p1 = 0 0 0 ;
*
tab1 = table 'BASE_MODALE' ;
TAB2 = TABLE 'BASE_DE_MODES' ;
TAB1 . MODES = TAB2 ;
TAB2 . 1 = TABLE 'MODE' ;
TAB2 . 1 .'POINT_REPERE' = PP1 ;
TAB2 . 1 . 'FREQUENCE' = 0 ;
TAB2 . 1 .'MASSE_GENERALISEE' = M1 ;
TAB2 . 1 .'DEFORMEE_MODALE' = manu chpo p1 1 ux 1. ;
*
** definition du chargement
w0 = .125*2*pi ;
list1 = prog 0. pas dt (t1/2-dt) ;
list2 = prog (t1/2) pas dt t1 ;
lisy1 = prog sinu .125 ampl (w0**2) list1 ;
lisy2 = prog sinu .125 ampl (1.5*(w0**2)) list2 ;
ev1 = evol manu 'temps' (list1 et list2)
'accel' (lisy1 et lisy2) ;
fx1 = force fx (-1*m1) p1 ;
cha1 = char fx1 ev1 ;
*
** chargement et cond. initiales en base A
cham1 = pjba tab1 cha1 ;
TCHA1 = TABLE 'CHARGEMENT' ;
TCHA1.'BASE_A' = CHAM1 ;
TINIT = TABLE 'INITIAL' ;
TINIT.'VITESSE' = manu chpo pp1 1 alfa w0 ;
*
** definition de la liaison
TLIA = TABLE 'LIAISON' ;
TLB = TABLE 'LIAISON_B' ;
TLIA.'LIAISON_B' = TLB ;
TL1 = TABLE 'LIAISON_ELEMENTAIRE' ;
TL1.'TYPE_LIAISON' = MOT 'POINT_PLAN';
TL1.'SUPPORT' = P1 ;
TL1.'NORMALE' = (1 0 0);
TL1.'RAIDEUR' = KE ;
TL1.'JEU' = 0.;
tl1.'SEUIL_PLASTIQUE' = se1 ;
TL1.'AMORTISSEMENT'= 0. ;
TLB. 1 = TL1 ;
*
** definition de la sortie
TSORT = TABLE 'SORTIE' ;
TSORL = TABLE 'LIAISON_B' ;
TSORT.'LIAISON_B' = TSORL ;
TSORL.TL1 = VRAI ;
*
** nombre de pas
npas = (enti (t1/dt)) ;
npas = npas / 2 ;
nins = 1 ;
*
** 1er bloc de calcul
tres1 = dyne differences_centrees tlia tab1 tcha1
tsort tinit npas dt nins;
TTL1 = TRES1.TL1 ;
LIS_TEM0 = TRES1.'TEMPS_DE_SORTIE';
lisxp1 = TTL1.'UX' ;
lisyp1 = ttl1 .'FORCE_DE_CHOC' ;
titre 'force - deplacement';
evdf1 = evol manu 'depl' lisxp1 'force' lisyp1 ;
titre 'deplacement plastique - temps' ;
evdp1 = evol manu 'temps' lis_tem0 'dep_pl'
ttl1.deplacement_plastique ;
*
** reprise de calcul
tinit = table initial ;
tinit.reprise = tres1.reprise ;
tres2 = dyne de_vogelaere tlia tab1 tcha1 tsort
tinit npas dt nins ;
TTL2 = TRES2.TL1 ;
LIS_TEM2 = TRES2.'TEMPS_DE_SORTIE';
lisxp2 = TTL2.'UX' ;
lisyp2 = ttl2 .'FORCE_DE_CHOC' ;
titre 'force - deplacement';
evdf2 = evol rouge manu 'depl' lisxp2 'force' lisyp2 ;
titre 'deplacement plastique - temps' ;
evdp2 = evol rouge manu 'temps' lis_tem2 'dep_pl'
ttl2.deplacement_plastique;
*
si (neg graph 'N');
titre 'force - deplacement';
dess (evdf1 et evdf2) ;
titre 'deplacement plastique - temps' ;
dess (evdp1 et evdp2) ;
finsi;
*
* maxima des deplacements plastiques theoriques
d11 = .5 ; d22 = 1.5 ;
mess
'max des depl. plastiques theoriques'd11' ' d22;
d1 = maxi (extr evdp1 ordo) ;
d2 = maxi (extr evdp2 ordo) ;
mess
'max des depl. plastiques C2000 'd1' ' d2 ;
er1 = abs(d1/d11 - 1); er2 = abs (d2/d22 - 1);
mess
'erreur 'er1'% 'er2'%';
err = maxi (prog er1 er2) ;
si (err > .005) ;
erre 5 ;
sinon ;
erre 0 ;
finsi;
fin ;
Test dy_devo6 Comments
TINIT = TABLE 'INITIAL' ;
TINIT.'VITESSE' = manu chpo pp1 1 alfa w0 ;
For this first block of the computation initial values must be given in TINIT table of INITIAL subtype. The load is defined on A basis, then the component of the initial values is alfa (A basis is related to uncoupled equations).
TLIA = TABLE 'LIAISON' ;
TLB = TABLE 'LIAISON_B' ;
TLIA.'LIAISON_B' = TLB ;
TL1 = TABLE 'LIAISON_ELEMENTAIRE' ;
TL1.'TYPE_LIAISON' = MOT 'POINT_PLAN';
TL1.'SUPPORT' = P1 ;
TL1.'NORMALE' = (1 0 0);
TL1.'RAIDEUR' = KE ;
TL1.'JEU' = 0.;
tl1.'SEUIL_PLASTIQUE' = se1 ;
TL1.'AMORTISSEMENT'= 0. ;
TLB. 1 = TL1 ;
TLIA is a table of subtype LIAISON.
TLIA.'LIAISON_B' (or TLB) is a table which gathers all linkages on B basis. This table has as many indexes as the number of linkages.
TLB.1 (or TL1) defines an elementary linkage. It is a table of 'LIAISON_ELEMENTAIRE' subtype. The first index to be specified is the type of the linkage (here 'POINT_PLAN').
The POINT-PLAN linkage allows to model the impact of a point onto a semi-infinite medium which is delimited by a fixed plane. The linkage is given in form of an imaginary spring which is defined by a stiffness (TL1.'RAIDEUR'), a yield limit (tl1.'SEUIL_PLASTIQUE') in case of plastification and a damping (TL1.'AMORTISSEMENT') in case of damping.
Other data is related to the impacting point (TL1.'SUPPORT'), the initial gap between the point and the fixed plane (TL1.'JEU'), the normal perpendicular to the plane and oriented towards the inside of the solid (TL1.'NORMALE').
** definition of output
TSORT = TABLE 'SORTIE' ;
TSORL = TABLE 'LIAISON_B' ;
TSORT.'LIAISON_B' = TSORL ;
TSORL.TL1 = VRAI ;
TSORT is the table of SORTIE subtype.
TSORT.'LIAISON_B' (or TSORL) is a table of LIAISON_B subtype and defines all linkages on B basis to be saved.
Every index of TSORL is the table defining the linkage to be saved (here TL1). The value of TSORL.TL1 is VRAI (true); thus all internal data of the linkage TL1 will be saved.
TTL1 = TRES1.TL1 ;
LIS_TEM0 = TRES1.'TEMPS_DE_SORTIE';
lisxp1 = TTL1.'UX' ;
lisyp1 = ttl1 .'FORCE_DE_CHOC' ;
titre 'force - displacement';
evdf1 = evol manu 'displ' lisxp1 'force' lisyp1 ;
titre 'plastic displacement - time' ;
evdp1 = evol manu 'time' lis_tem0 'disp_pl'
ttl1.deplacement_plastique ;
TRES.TL1 (or TTL1) is a table which contains the results related to the linkage defined in TL1 table.
- TTL1.'UX' is the list of UX displacements.
- ttl1 .'FORCE_DE_CHOC' is the list of the force of impact.
- ttl1.deplacement_plastique is the list of the plastic displacements.
tinit = table initial ;
tinit.reprise = tres1.reprise ;
tres2 = dyne de_vogelaere tlia tab1 tcha1 tsort tinit npas dt nins ;
For this second block of the computation initial values are defined in tinit.reprise. All data are given in the table tres1.reprise.