Test name
elas4
Calculation type
MECHANICS ELASTICITY 3D
Finite element type
COQ4
Topic
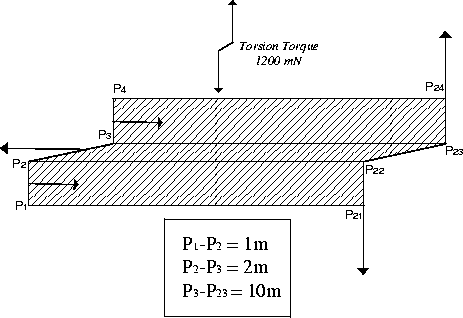
A cantilever beam wich cross section is subject to a torsion torque.
Consider a simple cantilever beam with a cross section. This structure is subjected to a torsion torque. The value of the torsion torque is 1200mN, obtained from two loads of 600N each. The loads are uniformly applied on each side.
Goal
Find the axial stress at point A(2.5, 0, 0). The analytical value is Smxx = -108 MPa.
Reference CASTEM
Test NAFEMS : ME8 : Modélisation des structures élastique dans CASTEM 2000.
Version
97' customer version
Model description

Test elas4 Results
RESULTS
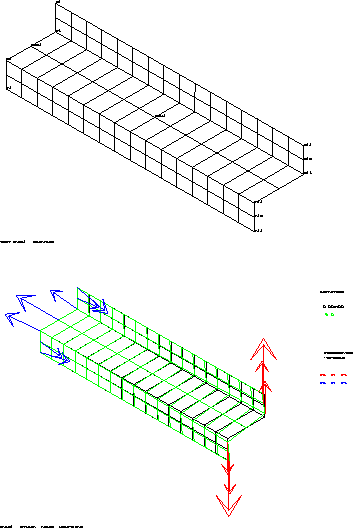
CASTEM figures
* Test Elas4.dgibi: Jeux de données *
* --------------------------------- *
*
* CAS TEST DU 91/06/13 PROVENANCE : TEST
SAUT PAGE;
*
*******************************************************
* *
* TEST ELAS4 *
* *
* POUTRE A SECTION EN FORME DE "Z" CHARGEE EN TORSION*
* *
* Cas test NAFEMS numero LE5 (Z-section cantilever) *
* *
* La poutre est maillee a l'aide d'elements de *
* coques COQ4. *
* Le maillage a ete affine car on ne peut utiliser *
* l'operateur CALP avec l'element COQ8. *
* *
* La poutre est soumis a un couple de torsion *
* de 1200 m.N, obtenue par deux forces de 600 N *
* uniformement reparties sur chaque flanc. *
* *
* On se propose de caculer la contrainte axiale *
* de la surface au point A. *
* *
*******************************************************
*
OPTI ECHO 0;
*
OPTI DIME 3;
OPTI ELEM QUA4;
*
GRAPH = 'N';
*
*======================================================*
* geometrie : maillage *
*======================================================*
*
* Dimension en metres
*
* Points
*
OEIL = 1000 -1000 1000;
*
P1 = 0 0 0; P21 = (P1 PLUS (10 0 0));
P2 = 0 0 1; P22 = (P2 PLUS (10 0 0));
P3 = 0 2 1; P23 = (P3 PLUS (10 0 0));
P4 = 0 2 2; P24 = (P4 PLUS (10 0 0));
*
P1M = 10 0 .5; P2M = 10 2 1.5;
*
* Droites et lignes
*
* Remarque : ne pouvant utiliser d'element coq8,
* et seulement des coq4 le maillage a ete affine.
*
N1 = 2;
LIG1 = P1 D N1 P2 D N1 P3 D N1 P4;
*
* Maillage
*
N2 = 16;
SUR1 = LIG1 TRANS N2 (10 0 0);
*
ELIM (SUR1 ET P21 ET P22 ET P23 ET P24 ET P1M ET P2M)
0.001;
*
SI (NEG GRAPH 'N');
TITR ' TEST ELAS4 : MAILLAGE ';
TRAC OEIL QUAL SUR1;
FINSI;
*
*====================================================*
* modele - materiau - caracteristique *
* rigidite - conditions aux limites *
*====================================================*
*
MODL1 = MODL SUR1 MECANIQUE ELASTIQUE ISOTROPE COQ4;
MATR1 = MATR MODL1 YOUN 210E9 NU 0.3 EPAI 0.1;
RI1 = RIGI MATR1 MODL1;
CL1 = BLOQ DEPL LIG1;
RIG1 = RI1 ET CL1;
*
*====================================================*
* Chargement *
*====================================================*
*
* Couple de torsion de 1.2e6 m.N applique dans la
* section x = 10 m par deux forces uniformement
* reparties egales de 600 N sur chaque flanc.
*
F1 = 0 0 -150E3;
F1M = 0 0 -300E3;
F2 = 0 0 150E3;
F2M = 0 0 300E3;
*
FORC1 = FORC F1 P21;
FORC2 = FORC F1 P22;
FORC1M = FORC F1M P1M;
FORC3 = FORC F2 P23;
FORC4 = FORC F2 P24;
FORC2M = FORC F2M P2M;
*
CHA1 = FORC1 ET FORC2 ET FORC3 ET FORC4 ET FORC1M ET
FORC2M;
*
*=====================================================*
* resolution : champs de deplacements *
* champs de contraintes *
*=====================================================*
*
DEP1 = RESO RIG1 CHA1;
*
* Trace facultatif de la deformee et des reactions
*
SI (NEG GRAPH 'N');
AMPVEC = .5E-6;
REA1 = REAC DEP1 RIG1;
VECT1 = VECT CHA1 (AMPVEC * 20) FX FY FZ ROUGE;
VECT2 = VECT REA1 AMPVEC FX FY FZ BLEU;
DEF0 = DEFO 0. DEP1 SUR1;
DEF1 = DEFO 5. DEP1 SUR1 (VECT1 ET VECT2) VERT;
TITR ' ELAS4 : Deformee, chargement, reactions';
TRAC OEIL SUR1 (DEF0 ET DEF1);
FINSI;
*
*======================================================*
* extraction d'une contrainte *
* et comparaison avec solution analytique *
*======================================================*
*
* On cherche la contrainte axiale au point A sur la
* surface moyenne.
*
* Calcul des contraintes generalisees dans le repere
* local des elements
*
CHAM1 = SIGM MODL1 MATR1 DEP1;
*
* Calcul du champs de contraintes au sens des milieux
* continus.
* Pour cela on utilise l'operateur CALP.
*
CHAM2 = CALP CHAM1 MATR1 MODL1 MOYEN;
CHAM3 = CHAN NOEUD CHAM2 MODL1;
CHPO3 = CHAN CHPO CHAM3 MODL1;
*
PA = SUR1 POIN PROC (2.5 0 0);
SMXXA2 = EXTR CHPO3 SMYY PA;
SMXXA2 = SMXXA2 / 1.E6;
SMXXA1 = -108;
ERGXXA = 100 * (ABS ((SMXXA2 - SMXXA1) / SMXXA1));
*
*=======================================================*
* affichage des resultats *
*=======================================================*
*
MESS ' RESULTATS TEST ELAS4 ';
MESS ' -------------------- ';
SAUT 2 LIGN;
MESS ' On cherche la contrainte axiale sur la surface
moyenne';
MESS ' au point A.';
MESS ' Elle est comparee a une valeur theorique obtenue';
MESS ' analytiquement.';
SAUT 1 LIGN;
SAUT 1 LIGN;
MESS ' Contrainte axiale theorique en A :' SMXXA1 'MPa';
MESS ' Contrainte axiale calculee en A :' SMXXA2 'MPa';
MESS ' Soit un ecart de :' ERGXXA '%';
SAUT 1 LIGN;
*
ELSUR1 = NBEL SUR1;
NOSUR1 = NBNO SUR1;
*
MESS ' Nombre d elements :' ELSUR1;
MESS ' Nombre de noeuds :' NOSUR1;
*
*========================================================*
* code fonctionnement *
*========================================================*
*
* L'ecart maximum entre valeur theorique et calculee
* doit etre inferieure a 5%.
*
SAUT 2 LIGNE;
SI (ERGXXA <EG 5);
ERRE 0;
SINON;
ERRE 5;
FINSI;
*
SAUT 1 LIGN;
TEMPS;
SAUT 1 LIGN;
*
FIN;
Test elas4 Comments
AMPVEC = .5E-6;
REA1 = REAC DEP1 RIG1;
VECT1 = VECT CHA1 (AMPVEC * 20) FX FY FZ ROUGE;
VECT2 = VECT REA1 AMPVEC FX FY FZ BLEU;
DEF0 = DEFO 0. DEP1 SUR1;
DEF1 = DEFO 5. DEP1 SUR1 (VECT1 ET VECT2) VERT;
TITR ' elas4 : STRAIN, LOADS, REACTIONS';
TRAC OEIL SUR1 (DEF0 ET DEF1);
The operator REAC(TION) constructs from the solution DEP1 the variation of the second member of the linear system relative to RIG1.
The operator VECT(EUR) constructs an object of VECTEUR type (VECT1 and VECT2) from the components of a field (CHA1 and REA1). The amplication coefficient must be given along with the names of the components (FX, FY, FZ).
The operator DEFO can be used by associating an object of VECTEUR type (VECT1 ET VECT2) with the object of DEFORME type. The result will represent the field of reactions by means of vectors in blue and the field of loads in red on the deformed shape drawing (in green).
CHAM1 = SIGM MODL1 MATR1 DEP1;
CHAM2 = CALP CHAM1 MATR1 MODL1 MOYEN;
CHAM3 = CHAN NOEUD CHAM2 MODL1;
CHPO3 = CHAN CHPO CHAM3 MODL1 ;
PA = SUR1 POIN PROC (2.5 0 0);
SMXXA2 = EXTR CHPO3 SMYY PA;
The operator SIGMA calculates a stress field (CHAM1) from a displacement field (DEP1). In the case of thin shell elements it is a matter of generalized stresses which are calculated in the local basis.
The operator CALP (CALcul en Peau) calculates a stress field in terms of continuum mechanics starting from a generalized stress field (CHAM1). In the case of shell elements the calculation is carried out at points obtained by projecting supporting points either onto the shell mid-plane (option chosen here with keyword MOYEN) or onto the top or bottom layer.
The operator CHAN(GER) constructs from a field by elements (CHAM2) and from a
model object (MODL1) a new field by elements (CHAM3) of the same kind as CHAM2 but born by the nodes (option taken here with keyword NOEUD).
The operator CHAN has different functions, the keyword CHPO loads it to construct from a field by elements and a model object a new field by points (CHPO3).
Note that the names of the components of the first stress field (CHAM1) are different from the names of components of the other stress fields.
ELSUR1 = NBEL SUR1;
NOSUR1 = NBNO SUR1;
The operator NBEL supplies the number of elements contained in the geometry SUR1. In the same way, the operator NBNO supplies the number of nodes contained in the geometry SUR1.