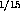Test name
rupt6
Calculation type
MECHANICS ELASTIC
Finite element type
CU20 MODE TRID
Topic
STRESS INTENSITY FACTOR FOR A CIRCULAR
PLANE CRACK IN AN INFINITE SOLID CYLINDER
SUBJECTED TO TENSILE STRESS
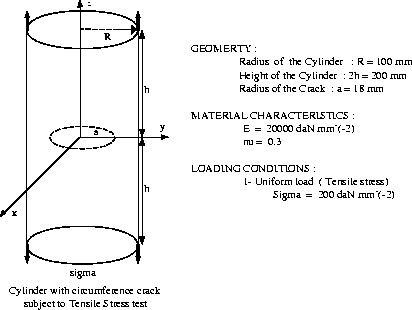
The structure is an infinite solid cylinder tube enclosing a central circular crack . This structure is subject to tensile stress.
Due to symmetry only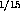 
of half of the cylinder is analysed. The CASTEM solution for the stress intensity factors K is given
with the displacement method by the relationship ( threedimensional analysis) :
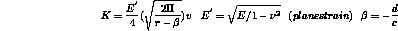
c and d are the coefficients of the line :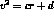 
Finally this CASTEM K value for the stress intensity factor is compared with the result obtained with the
analytical formula defined by the relationship :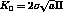 
Reference CASTEM
Test NAFEMS : D.P.Rooke and D. J. Cartwright in Copendium of Intensity Factors HMSO (1976) :
rupt6 Modélisation des structures élastiques dans CASTEM 2000.
Version
97' customer version
Model description
Test rupt6 Results
RESULTS
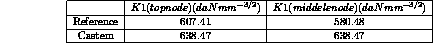
CASTEM FIGURES
* Test Rupt6.dgibi: Jeux de données *
* --------------------------------- *
* *
*******************************************************
*** CALCUL DU FACTEUR D'INTENSITE DE CONTRAINTES ****
*** PAR LA METHODE DES DEPLACEMENTS ET PAR LA ****
*** METHODE G_THETA POUR UNE FISSURE CIRCULAIRE ****
*** PLANE DANS UN MILIEU INFINI CHARGE EN ****
*** TRACTION UNIFORME ****
*** HAUTEUR DU CYLINDRE : 200 mm ; ****
*** RAYON : 100 mm ****
*** RAYON DE FISSURE : 8 mm ; ****
*** CONTRAINTE UNIFORME : 200 daN / mm2 ****
*** MODELISATION : TRANCHE DE 15° DE LA 1/2 ****
*** HAUTEUR DU CYLINDRE ****
*******************************************************
option echo 0 dime 3 elem cu20 mode trid ;
**----------------- MAILLAGE ------------------;
dens 0.5 ;
oeilz = -500 500 -500 ;
oeilx = -500 00 00 ;
a0 = 8 ;
c0 = 16. ;
b0 = 100. ;
p0 = 0 0 0 ;
pa = a0 0 0 ;
pb = 0 a0 0 ;
pa1 =(1.5*a0) 0 0 ;
pa0 =(0.5*a0) 0 0 ;
pb0 = 0 (0.5*a0) 0 ;
pb1 = 0 (1.5*a0) 0 ;
* nbrz nombre d element autour du front de fissu;
nbrz = 6 ;
*MAILLAGE DU FRONT DE FISURE ;
pbz= (0. a0 (0.5*a0)) ;
pbz1=(0. (a0 *(1.- (0.5 / nbrz))) 0.) ;
pbz2=(0. a0 (0.5*a0/ nbrz)) ;
pbz3=(0. (a0 *(1.+ (0.5 / nbrz))) 0.) ;
aa = a0*0.5 * (2**-0.5) ;
pmi1= 0. (a0 + aa) aa ;
pmi2= 0. (a0 - aa) aa ;
cc11a = c (2) pb1 pb pmi1 ;
cc11b = c (2) pmi1 pb pbz ;
cc11 = cc11a et cc11b ;
cc12a = c (2) pbz pb pmi2 ;
cc12b = c (2) pmi2 pb pb0 ;
cc12 = cc12a et cc12b ;
cc1 = cc11 et cc12 ;
cc21 = c (4) pbz1 pb pbz2 ;
cc22 = c (4) pbz2 pb pbz3 ;
cc2 = cc21 et cc22 ;
ligz = d (nbrz - 1) pb0 pbz1 ;
ligz1= d (nbrz - 1) pbz3 pb1 ;
ligz2= d (nbrz - 1) pbz pbz2 ;
scz1 = dall cc11 ligz2 cc22 ligz1 ;
scz2 = dall cc12 ligz cc21 (inve ligz2) ;
scz1=scz1 et (cout cc22 pb) ;
scz2=scz2 et (cout cc21 pb) ;
scz =scz1 et scz2 ;
elim (scz1 et scz2) 0.001 ;
* SURFACE YZ ;
pfinay = 0. b0 0. ;
pfinaz = 0. 2.5 b0 ;
pfinayz= 0. b0 b0 ;
pinter = 0. (2*c0) b0 ;
pp = 0. a0 a0 ;
pz = 0. 2.5 a0 ;
p00= 0. 2.5 0. ;
ppp= 0. (2*a0) 0. ;
ppyz= 0. (2*a0) a0 ;
l0a= d (1) pb1 ppp ;
l0b= d (6) ppp pfinay ;
l0 = l0a et l0b ;
l1 = d (2) pfinay pfinayz ;
l1bisa = d (6) pfinayz ppyz ;
l1bisb = d (1) ppyz pmi1 ;
l1bis = l1bisa et l1bisb ;
l2 = d (2) pfinayz pinter ;
l3a = d (6) pinter pp ;
l3b = d (1) pp pbz ;
l3 = l3a et l3b ;
zaa = dall (inve cc11a) l0 l1 l1bis ;
zab = dall l1bis cc11b (inve l3) (inve l2) ;
za = zaa et zab ;
g2= d (1) pb0 p00 ;
g3= d (2) p00 pz ;
g4= d (2) pz pp ;
zb =dall (g4 et g3) g2 cc12 l3b ;
h1 = d (2) pinter pfinaz ;
h2 = d (6) pfinaz pz ;
zc = dall h2 g4 l3a h1 ;
scr1 = h2 et (inve g3) ;
*CREATION DU VOLUME ;
scr1 = scr1 rota 1 (15) (0. 0 -500)
(0 0 500.) coul roug ;
geo1 = za volu 1 'ROTA' (15)
(0. 0. -500) (0. 0. 500.) ;
geo2 = (zb et zc) volu 1 'ROTA' (15)
(0. 0. -500) (0. 0. 500.) ;
geo3 = scz1 volu 1 'ROTA' (15)
(0. 0. -500) (0. 0. 500.) ;
geo4 = scz2 volu 1 'ROTA' (15)
(0. 0. -500) (0. 0. 500.) ;
i = face 3 geo3 ;
i = i et (face 3 geo4) ;
pppp = i poin cylin (0 0 -100) (0 0 100) pb ;
aa0= elem i appu larg pppp ;
aa1= poin aa0 plan p0 (0. 100 0.) (100 0 0) ;
cfis = elem aa0 appu stric aa1 ;
a1 = enve geo3 ;
a2 = enve geo4 ;
aa1= poin a1 plan p0 (0. 100 0.) (100 0 0) ;
aa2= poin a2 plan p0 (0. 100 0.) (100 0 0) ;
aa11 = elem a1 appu stric aa1 ;
aa21 = elem a2 appu stric aa2 ;
aa12 = cont aa11 ;
aa22 = cont aa21 ;
elim (aa12 et aa22) 0.001 ;
cfissure = elem aa12 appu stric aa22;
geo = geo1 et geo2 et geo3 et geo4 ;
elim (geo et scr1 et cfissure et cfis) 0.001 ;
*FINITION DU MAILLAGE ;
*pres de l axe z ;
c1 = cote (2) scr1 ;
pfi = c1 poin final ;
c1x = droi (1) pfi p0 ;
b1 = droi (1) p00 p0 ;
su0 = surf ( c1x et c1 et b1) plane ;
su1 = su0 volu (2) tran (0. 0. a0) ;
ss = su0 plus (0. 0. b0) ;
su2= ss volu (6) tran (0. 0. (a0 - b0)) ;
su = su1 et su2 coul vert ;
*le cylindre en entier ;
cub = geo et su ;
elim cub 0.001 ;
cub = rege cub ;
tot = enve cub ;
*surface yz ;
poyz = poin tot plan p0 (0. 100 100) (0. 0. 100);
suryz = elem tot appu stric poyz ;
*surface z=100 ;
poz100= poin tot plan (0. 0. 100)
(100 0. 100) (0. 100 100) ;
surzz = elem tot appu stric poz100 ;
*surfac xy ;
poxy = poin tot plan p0 (0. 100 0.) (100 0 0) ;
surxy= elem tot appu stric poxy ;
az = geo2 et geo4 et su ;
az = enve az ;
aze= az poin plan p0 (0. 100 0.) (100 0 0) ;
aze=elem az appu stric aze ;
co = cont aze;
aze = surxy incl aze;
facxy = surxy diff aze;
*--------------CONDITION DE SYMETRIE------------;
p = ((-1 * b0 * (sin 15)) (b0 * (cos 15)) 0.);
condi1 =symt depl p0 (0. 0. b0) p cub 0.01;
condi2 =symt depl p0 pfinay pfinayz suryz;
condi3 =symt depl p0 (b0 b0 0.) (b0 0. 0.) facxy;
condit = condi1 et condi2 et condi3 ;
*----------- CREATION DU MODELE ----------------;
affe1 = modl geo1 mecanique elastique isotrope;
affe2 = modl geo2 mecanique elastique isotrope;
affe3 = modl geo3 mecanique elastique isotrope;
affe4 = modl geo4 mecanique elastique isotrope;
affe5 = modl su mecanique elastique isotrope;
affetot = affe1 et affe2 et
affe3 et affe4 et affe5 ;
*---------DEFINITION DU MATERIAU ---------------;
mate1 = matr affe1
young 20000.
nu 0.3 ;
mate2 = matr affe2
young 20000.
nu 0.3 ;
mate3 = matr affe3
young 20000.
nu 0.3 ;
mate4 = matr affe4
young 20000.
nu 0.3 ;
mate5 = matr affe5
young 20000.
nu 0.3 ;
matot = mate1 et mate2 et
mate3 et mate4 et mate5 ;
*----------------RIGIDITE-----------------------;
rig1 = (rigidite matot affetot) et condit ;
rig2 = bloque uz surzz ;
fo1 = depi rig2 1. ;
*------------RESOLUTION ET CONTRAINTES----------;
dep = resou (rig1 et rig2) fo1 ;
sig = sigma matot affetot dep ;
*----CALCUL DU FACTEUR D'INTENSITE DE CONTRAINTES----*
*----initialisations des paramètres de procedure-----*
SUPTAB = TABLE;
SUPTAB.'MAILLAGE' = cub;
SUPTAB.'PSF1' = P0;
SUPTAB.'FRTFISS' = elem aa12 appu stri aa22;
*-----APPEL DE LA PROCEDURE SIF ----------------------*
SIF SUPTAB MATOT dep;
*-----APPEL DE LA PROCEDURE G_THETA ------------------*
TABG1 = TABLE;
TABG1.'OBJECTIF' = MOT 'J';
TABG1.'COUCHE' = 3;
TABG1.'FRONT_FISSURE' = cfissure;
TABG1.'LEVRE_SUPERIEURE' = aa21 ;
TABG1.'MODELE' = affetot;
TABG1.'SOLUTION_RESO' = dep;
TABG1.'CHARGEMENTS_MECANIQUES' = fo1;
TABG1.'CARACTERISTIQUES' = matot;
G_THETA TABG1;
SAUT 1 LIGNE;
*******************************************************
******** DEPOUILLEMENT PROCEDURE SIF *************
*******************************************************
T = INDEX (SUPTAB.K1);
MESS 'K1 NOEUD 1 DU FRONT DE FISSURE (NOEUD SOMMET) : '
SUPTAB.K1.(T.1);
MESS 'K1 NOEUD 2 DU FRONT DE FISSURE (NOEUD MILIEU) : '
SUPTAB.K1.(T.2);
*---------TEST D'ERREUR-----------------------------*
EC1 = ((SUPTAB.K1.(T.1)) - 638.47) /
(SUPTAB.K1.(T.1)) * 100;
EC2 = ((SUPTAB.K1.(T.2)) - 638.47) /
(SUPTAB.K1.(T.2)) * 100;
SI ((EC1 < 5.5) ET (EC2 < 11)) ;
MESS 'PROCEDURE <SIF> ERR 0';
ERRE 0;
SINON;
MESS 'PROCEDURE <SIF> ERR 5';
ERRE 5;
FINSI;
*******************************************************
******** DEPOUILLEMENT PROCEDURE G_THETA *********
*******************************************************
TBG = TABG1.'RESULTATS';
IND1 = INDE TBG;
GSOM = TBG.(IND1.1);
GMIL = TBG.(IND1.2);
EPRI = 20000. / 0.91;
KSOM = (GSOM * EPRI) ** 0.5;
KMIL = (GMIL * EPRI) ** 0.5;
SAUT 1 LIGNE;
MESS 'K1 NOEUD 1 DU FRONT DE FISSURE (NOEUD SOMMET) : '
KSOM;
MESS 'K1 NOEUD 2 DU FRONT DE FISSURE (NOEUD MILIEU) : '
KMIL;
*---------TEST D'ERREUR-----------------------------*
EC1 = ABS (((KSOM - 638.47) / KSOM) * 100);
EC2 = ABS (((KMIL - 638.47) / KMIL) * 100);
SI ((EC1 < 0.9) ET (EC2 < 0.8)) ;
MESS 'PROCEDURE <G_THETA> ERR 0';
ERRE 0;
SINON;
MESS 'PROCEDURE <G_THETA> ERR 5';
ERRE 5;
FINSI;
FIN;
Test rupt6 Comments
DESCRIPTION OF THE SIF PROCEDURE
SIF SUPTAB MATOT DEP;
Input data :
SUPTAB : TABLE type object, indexed by words, used to define
the calculation options and parameters :
MATOT : field of material properties
DEP : displacement field
SUPTAB : TABLE type object, indexed by words, used to define
the calculation options and parameters :
SUPTAB = TABLE; SUPTAB.'MAILLAGE' = cub; SUPTAB.'PSF1' = P0; SUPTAB.'FRTFISS' = elem aa12 appu stri aa22;'PSF1'=P0; : point of the crack surface that does not pertain to the front
'FRTFISS'= elem aa12 appu stri aa22; : line describing the front crack
T = INDEX (SUPTAB.K1);
MESS 'K1 NODE 1 FOR THE CRACK TIP (TOP NODE) : '
SUPTAB.K1.(T.1);
MESS 'K1 NODE 2 FOR THE CRACK TIP (MIDDEL NODE) : '
SUPTAB.K1.(T.2);
K1 : TABLE containing the values of K1 at each node of the front (here at 2 nodes T.1 and T.2)