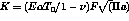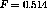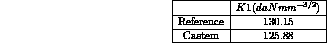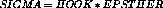Next: Test rupt3 Description
Up: FRACTURE MECHANICS
Previous: Test rupt1 Description
Test name
rupt2
Calculation type
ELASTIC MECHANICS
Finite element type
QUA8 PLANE STRAIN MODE
Topic
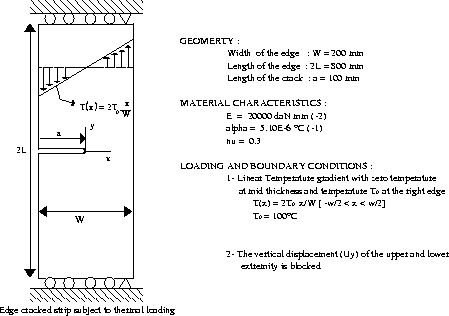
THE USE OF G-INTEGRAL IN THERMAL STRESS FOR AN EDGE CRACKED STRIP
The structure is a solid edge cracked strip which ends are constrained. It is subject to a linear temperature
gradient through the thickness with zero temperature at mid-thickness and temperature 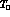 at the right edge
at the right edge
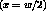 .
.
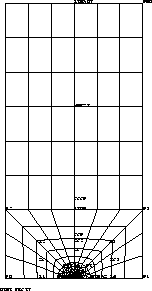
Due to symmetry only one half of the strip is analysed. The CASTEM solution for the stress intensity factor K is given
by the relationship :
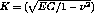
Finally the K values for 7 differente temperatures  are computed and compared with the
results obtained with WILSON and YU relationship :
are computed and compared with the
results obtained with WILSON and YU relationship :
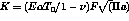
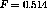
Reference CASTEM
Test NAFEMS : The use of J-integral in thermal stress crack problems International Journal of Fracture :
rupt2 Modélisation des structures élastiques dans CASTEM 2000.
Version
97' customer version
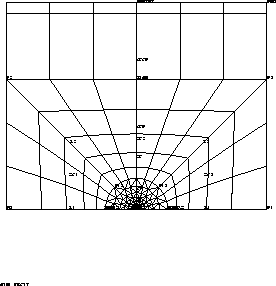
Model description
Test rupt2 Results
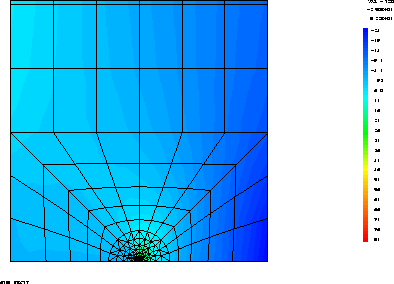
RESULTS
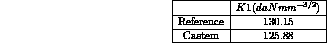
CASTEM FIGURES
Test rupt2 Results

* Test Rupt2.dgibi: Jeux de données *
* --------------------------------- *
* *
OPTION ECHO 0 ;
GRAPH = 'N' ;
SAUT PAGE ;
* ;
******************************************************;
* ;
* ;
* QUALIFICATION DU CALCUL DE G ;
* EN THERMO-ELASTICITE LINEAIRE ;
* SUR UNE PLAQUE A FISSURE LATERALE ;
* EVALUATION DU FACTEUR DE FORME ;
* ;
* ;
* le calcul est compare a celui obtenu par ;
* WILSON et YU ;
* dans The use of J-Integral in thermal stress crack ;
* problems international Journal of Fracture (1979) ;
* ;
******************************************************;
* ;
OPTION DIME 2 ELEM QUA8 MODE PLAN DEFO ;
* ;
*----------------- DEFINITION DU MAILLAGE ------------;
* ;
a = 100. ; b = 200. ; h = 400. ;t = a / 100. ;
densite t ; pf = (a 0.) ;
c1 = (c ( pf moin (t 0.)) pf ( pf plus (0. t)))
c pf ( pf plus (t 0.)) ;
sf = cout pf c1;
r1 = t ; rr1 = t ;
repeter bhomo 7;
ri = r1 + ( 0.3 * r1 ) ;
rri = rr1 + ri ;
dens ri ;
ci = ( c ( pf moin (rri 0.)) pf ( pf plus (0. rri)))
c pf ( pf plus (rri 0.)) ;
sf = sf et ( cout c1 ci ) ;
c1 = ci ; r1 = ri ; rr1 = rri ;
fin bhomo ;
dens (a / 3.) ;
p0 = (0. 0.) ; p1 = (b 0.) ;
p2 = p0 plus (0. a) ; p3 = p1 plus (0. a) ;
pi1 = ci poin 1 ; l1 = pi1 d p0 ;
n = (nbel l1) * -1 ;
pi2 = ci poin 4 ; l2 = pi2 d n p2 ;
pi3 = ci poin 10 ; l3 = pi3 d n p3 ;
pi4 = ci poin 13 ; l4 = pi4 d p1 ;
ci = inve ci ;ligh = p2 d p3 ;
sc1 = dall l1 (p0 d p2) (inve l2) (ci comp pi2 pi1) ;
sc2 = dall l2 ligh (inve l3) (ci comp pi3 pi2) ;
sc3 = dall l3 (p3 d p1) (inve l4) (ci comp pi4 pi3) ;
sc = sc1 et sc2 et sc3 ;
dens (a / 2.) ;
mrest = ligh tran (0. (h - a)) dini (a / 2.) ;
lihaut = mrest cote 3 ;
phd = lihaut poin init ;
ccp = sf et sc et mrest ;
elim ccp 0.001 ;
cccp = cont ccp ;
lifis = cccp comp pf p0 ;
libas = cccp comp p1 pf ;
* ;
*------------------- CREATION DU MODELE --------------;
* ;
objaf = modl ccp mecanique elastique isotrope ;
* ;
*---------- DEFINITION DES CARACTERISTIQUES ----------;
*---------- MATERIELLES ET GEOMETRIQUES ----------;
* ;
mat = matr objaf YOUN 2.e4 NU 0.3 ALPH 5.e-6 ;
* ;
*---------- CALCUL DES RIGIDITES ELEMENTAIRES --------;
*--------- ET DEFINITION DES BLOCAGES ---------;
* ;
rig = rigi objaf mat ;
cdl1 = bloq Uy libas ;
cdl2 = bloq Uy lihaut ;
cdl3 = bloq Ux phd ;
* ;
*-------- DEFINITION DU CHAMP DE TEMPERATURES --------;
* ;
chx = coor 1 ccp ;
cha = manu chpo ccp 1 scal a ;
chx = nomc 'T' (chx - cha) ;
cht = chx * (100. / a) ;
ch0 = 0 * cht ;
sigth = thet MAT objaf cht ;
* ;
*-------- RESOLUTION ET CALCUL DES CONTRAINTES -------;
* ;
U = reso (rig et cdl1 et cdl2 et cdl3 )
(bsig objaf sigth) ;
SIG = sigm mat objaf U ;
SIG = SIG - sigth ;
sigy = exco SIG smyy ;
SI ( NEG GRAPH 'N' ) ;
TRAC CCP ;
TRAC SIGY OBJAF CCP ;
FINSI ;
* ;
*------ INITIALISATION DE LA TABLE EN ENTREE ---------;
*---- DE LA PROCEDURE G_THETA ----------;
* ;
SUPTAB = TABLE ;
SUPTAB.'OBJECTIF' = MOT 'J';
SUPTAB.'LEVRE_SUPERIEURE' = lifis;
SUPTAB.'FRONT_FISSURE' = PF ;
SUPTAB.'MODELE' = objaf;
SUPTAB.'CARACTERISTIQUES' = mat;
SUPTAB.'SOLUTION_RESO' = u;
SUPTAB.'TEMPERATURES' = cht;
SUPTAB.'COUCHE' = 4;
* ;
*----------- APPEL A LA PROCEDURE G_THETA ------------;
* ;
SAUT PAGE ;
G_THETA suptab ;
* ;
*------ RECUPERATION DU RESULTAT ET COMPARAISONS -----;
* ;
G = suptab.'RESULTATS' ;
K = (20000. * G / (1 - (0.3**2)))**0.5 ;
F = K * (1 - 0.3) /
( 20000 * 5.e-6 * 100 * ((100*pi)**0.5)) ;
mess 'taux de restitution energetique G :' G ;
mess 'coefficient d intensite de contrainte K :' K ;
mess 'facteur de forme calcule Fcal :' F ;
mess
'facteur de forme analytique Fthe :' 0.514 ;
* CODE FONCTIONNEMENT ;
RESI = abs (( F - 0.514 ) / 0.514 ) ;
SI (RESI < 5E-2) ;
ERRE 0 ;
SINO ;
ERRE 5 ;
FINSI ;
fin;
Test rupt2 Comments
- DEFINITION OF THE LINEAR TEMPERATURE GRADIENT
chx = coor 1 ccp ;
cha = manu chpo ccp 1 scal a ;
chx = nomc 'T' (chx - cha) ;
cht = chx * (100. / a) ;
ch0 = 0 * cht ;
sigth = thet MAT objaf cht ;
- COOR OPERATOR :
The COOR operator enables the user to recover the Nith coordinate (for this example it is the first coordinate N=1)
of a POINT, MAILLAGE, CHPOINT or MCHAML object type (here CCP is a MAILLAGE (MESH) type).
For a CCP mesh object type, the operator supplies the coordinates of the nodes supporting the mesh.
- MANU OPERATOR :
The MANU operator enables the user to simply create objets of the following types : MAILLAGE, CHPOINT, SOLUTION,
RIGIDITE. here the MANU operator constructs a field by point by means of the key word 'CHPO'. :
CCP is the geometrical support (MAILLAGE type)
1 is the number of components of the field by points (ENTIER type)
SCAL is a name of components (MOT type) not exceeding 4 characters
a is a list of the value allocated to each node of CCP.
- NOMC OPERATOR :
The NOMC operator enables the user either to change the component na of a field by points
or to replace a sublist of components by a second one :
(chx - cha) is CHPO1 field by points (CHPOINT type) and 'T' (Temperature) is a new name allocated
to the component (MOT type) . CHX is the generated object (CHPOINT type) .
NOTE :
The field by points CHPO1 must be composed of a single component
which name is arbitrary.
- THET OPERATORS :
The THETA operator calculates the stresses associated with a
temperature field, i.e. :
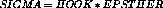
in which HOOK is Hooke's matrix and EPSTHER corresponds to the strains of thermal origin :
sigth = thet MAT objaf cht
MAT is a field of material and geometrical properties (MCHAML type, CARACTERISTIQUES subtype)
OBJAF is a model object (MMODEL type)
CHT is a temperature field (CHPOINT type).
SIGTH is a stress field (MCHAML type, CONTRAINTES subtype).
Note :
For the shell elements, the temperature field must have three
components with the following names : TINF ,T, and TSUP which
define respectively the temperature on the bottom , mid-surface
and top layers. For the other elements, the temperature field must have one
component with the following name : T. You may recover the thermal strains from the thermal stresses
using the ELAS operator.
- RESOLUTION G_THETA PROCEDURE
The CASTEM solution for the stress intensity factors K is given by the G_THETA PROCEDURE
from the relationship :
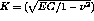
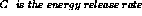




Next: Test rupt3 Description
Up: FRACTURE MECHANICS
Previous: Test rupt1 Description
ven 3 nov 04:14:58 NFT 2000
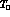 at the right edge
at the right edge
 .
.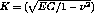
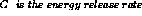
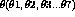 are computed and compared with the
results obtained with WILSON and YU relationship :
are computed and compared with the
results obtained with WILSON and YU relationship :