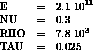
Test name
preston1
Calculation type
ISOTROPIC ELASTOPLASTIC MECHANICS
Finite element type
CUB8
Topic
Preston Tonks Wallace model
The structure is a beam embedded at the lower and
upper surface. It is subjected to tensile strength
(imposed displacements) at the end. The beam follows
an elastoplastic law according to the
Preston-Tonks-Wallace model.
Goal
Test the Preston Tonks Wallace model for BCC 3
structure.
Version
97' customer release
Model description
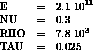
* Test Preston1.dgibi: Jeux de données *
* ------------------------------------ *
* *
complet = faux;
*
*************************************************
* pour calcul complet mettre complet à : vrai;
*************************************************
**************************************************
* *
* TEST DE VALIDATION D'UNE LOI DE COMPORTEMENT *
* -------------------------------------------- *
* DE MATERIAU *
* ----------- *
* *
* LOI DE COMPORTEMENT DE: *
* PRESTON TONKS WALLACE *
* CAS CUBIQUE CENTRE ( C.C. ) *
* *
* MAILLAGE: *
* UNE BARRE DE SECTION CARREE *
* LONGUEUR L=.5 M *
* LARGEUR l=.001 M *
* *
* CHARGEMENT: *
* ESSAI DE TRACTION *
* DEPLACEMENTS IMPOSES *
* *
**************************************************
*
opti echo 0 dime 3 elem cub8 ;
*
*
* Maillage
*
l1 = .5 ;
l2 = .001 ;
l3 = .001 ;
n1 = 50 ;
n2 = 1 ;
n3 = 1 ;
p1 = 0. 0. 0. ;
p2 = l1 0. 0. ;
p3 = l1 l2 0. ;
p4 = 0. l2 0. ;
p5 = 0. 0. l3 ;
p6 = l1 0. l3 ;
p7 = l1 l2 l3 ;
p8 = 0. l2 l3 ;
d1 = d p1 n3 p5 ;
d2 = d p5 n2 p8 ;
d3 = d p8 n3 p4 ;
d4 = d p4 n2 p1 ;
sur1 = 'DALL' d1 d2 d3 d4 ;
d5 = d p2 n3 p6 ;
d6 = d p6 n2 p7 ;
d7 = d p7 n3 p3 ;
d8 = d p3 n2 p2 ;
sur2 = 'DALL' d5 d6 d7 d8 ;
vol1 = sur1 'VOLU' n1 sur2 ;
*
* Modele de calcul
*
mod0 = 'MODE' vol1 'MECANIQUE' 'ELASTIQUE' 'ISOTROPE'
'PLASTIQUE' 'PRESTON' ;
mat0 = 'MATE' mod0 'YOUN' 2.1E11 'NU' 0.3
'RHO' 7.8E3 'TAU' 0.025
'P' 0. 'S0' 0.0085 'SINF' 0.00055
'K' 0. 'G' 0.00001
'Y0' 0.0001 'YINF' 0.0001 'Y1' 0.094 'Y2' 0.575
'BETA' 0.25 'GP' 3.00 'GT' 0. 'MU' 1.97
'TMO' 1220. ;
*
* Conditions aux limites
*
cl1 = 'BLOQ' sur1 'UX' ;
cl2 = 'BLOQ' sur2 'UX' ;
cl3 = 'BLOQ' p1 'UX' 'UY' 'UZ' ;
cl4 = 'BLOQ' p5 'UX' 'UY' ;
cl0 = cl1 'ET' cl2 'ET' cl3 'ET' cl4 ;
*
* Chargement
*
dep1 = 'DEPI' cl2 .1 ;
ev0 = 'EVOL' 'MANU' temps ( 'PROG' 0. 5.E-4 ) y
( 'PROG' 0. 1. ) ;
cha0 = 'CHAR' 'DIMP' dep1 ev0 ;
*
* Temps du calcul
*
dt0 = 1.E-5 ;
si complet;
tfin0 = 5.E-4 ;
sinon;
tfin0 = 4.e-5;
finsi;
*
*
* Resolution par PASAPAS
*---------------------------------------
*
ta1 = 'TABLE' ;
ta1 .'MODELE' = mod0 ;
ta1 .'CARACTERISTIQUES' = mat0 ;
ta1 .'BLOCAGES_MECANIQUES' = cl0 ;
ta1 .'CHARGEMENT' = cha0 ;
*ta1 .'PRECISION' = 1.E-8 ;
ta1 .'TEMPS_CALCULES' = 'PROG' 0. 'PAS' dt0 tfin0 ;
*
PASAPAS ta1 ;
*
*
* Post-traitement
*-----------------------------------------
*
sig_3dy = 'PROG' 0. ;
sig_3dz = 'PROG' 0. ;
sigx1 = 'PROG' 0. ;
sigx2 = 'PROG' 0. ;
depx1 = 'PROG' 0. ;
depx2 = 'PROG' 0. ;
sig_1 = 'PROG' 0. ;
def_1 = 'PROG' 0. ;
epsp1 = 'PROG' 0. ;
err1 = 'PROG' 0. ;
err2 = 'PROG' 0. ;
sig1 = 'PROG' 0. ;
temp1 = 'PROG' 0. ;
epst1 = 'PROG' 0. ;
dim0 = 'DIME' ta1 .'TEMPS' - 1 ;
mod0 = ta1 .'MODELE' ;
YOUNG0 = 'EXCO' mat0 'YOUNG' 'SCAL' ;
YOUNG1 = 'MAXI' YOUNG0 ;
XNU0 = 'EXCO' mat0 'NU' 'SCAL' ;
XNU1 = 'MAXI' XNU0 ;
RHO0 = 'MAXI' ( 'EXCO' mat0 'RHO' 'SCAL' ) ;
TAU0 = 'EXCO' mat0 'TAU' 'SCAL' ;
TAU1 = 'MAXI' TAU0 ;
P1 = 'EXCO' mat0 'P' 'SCAL' ;
P11 = 'MAXI' P1 ;
S0 = 'EXCO' mat0 'S0' 'SCAL' ;
S01 = 'MAXI' S0 ;
SINF0 = 'EXCO' mat0 'SINF' 'SCAL' ;
SINF1 = 'MAXI' SINF0 ;
K0 = 'EXCO' mat0 'K' 'SCAL' ;
K1 = 'MAXI' K0 ;
G0 = 'EXCO' mat0 'G' 'SCAL' ;
G1 = 'MAXI' G0 ;
Y00 = 'EXCO' mat0 'Y0' 'SCAL' ;
Y01 = 'MAXI' Y00 ;
YINF0 = 'EXCO' mat0 'YINF' 'SCAL' ;
YINF1 = 'MAXI' YINF0 ;
Y10 = 'EXCO' mat0 'Y1' 'SCAL' ;
Y11 = 'MAXI' Y10 ;
Y20 = 'EXCO' mat0 'Y2' 'SCAL' ;
Y21 = 'MAXI' Y20 ;
BETA0 = 'EXCO' mat0 'BETA' 'SCAL' ;
BETA1 = 'MAXI' BETA0 ;
GP0 = 'EXTR' ( 'EXCO' mat0 'GP' 'SCAL' ) 'SCAL' 1 1 1 ;
GT0 = 'EXTR' ( 'EXCO' mat0 'GT' 'SCAL' ) 'SCAL' 1 1 1 ;
A1 = 2. * ( 1. + XNU1 ) ;
B1 = A1 / ( 3. * ( 1. - ( 2. * XNU1 ) ) ) ;
'REPETER' bloc1 dim0 ;
i1 = &bloc1 ;
depl0 = ta1 .'DEPLACEMENTS'.i1 ;
temp0 = ta1 .'TEMPS'.i1 ;
temp1 = temp1 'ET' ( 'PROG' temp0 ) ;
dex1 = 'EXCO' depl0 'UX' 'SCAL' ;
dex0 = 'EXCO' ta1 .'DEPLACEMENTS'.( i1 - 1 )
'UX' 'SCAL' ;
reac0 = ta1 .'REACTIONS'.i1 ;
reac1 = 'MAXI' ( 'EXCO' reac0 'FX' 'SCAL' ) ;
dep0 = 'MAXI' dex0 ;
dep1 = 'MAXI' dex1 ;
eps1 = 'EPSI' mod0 depl0 ;
epsx1 = 'EXCO' eps1 'EPXX' 'SCAL' ;
epsy1 = 'EXCO' eps1 'EPYY' 'SCAL' ;
epsz1 = 'EXCO' eps1 'EPZZ' 'SCAL' ;
treps0 = 'MAXI' ( epsx1 + epsy1 + epsz1 ) ;
epsx10 = 'MAXI' epsx1 ;
sigm0 = ta1 .'CONTRAINTES'.i1 ;
depeq0 = ta1 .'VARIABLES_INTERNES'.i1 ;
def0 = ta1 .'DEFORMATIONS_INELASTIQUES'.i1 ;
t1 = ta1 .'TEMPS'.i1 ;
t0 = ta1 .'TEMPS'.(i1 - 1) ;
dt0 = t1 - t0 ;
dt0 = 0. ;
'SI' ( ( 'ABS' dt0 ) < 1.E-10 ) ;
deps0 = 0. ;
'SINON' ;
deps0 = ( dep1 - dep0 ) / ( dt0 * l1 ) ;
'FINSI' ;
*
sigx0 = 'MAXI' ( 'VMIS' mod0 sigm0 ) ;
sigx00 = 'MINI' ( 'VMIS' mod0 sigm0 ) ;
depx0 = 'MAXI' ( 'EXCO' depeq0 'EPSE' 'SCAL' ) ;
depx00 = 'MINI' ( 'EXCO' depeq0 'EPSE' 'SCAL' ) ;
sig_00 = 'EXCO' sigm0 'SMXX' 'SCAL' ;
sig_0 = 'MAXI' sig_00 ;
eps_el0 = sig_0 / YOUNG1 ;
sig_y = 'MAXI' ( 'EXCO' sigm0 'SMYY' 'SCAL' ) ;
sig_z = 'MAXI' ( 'EXCO' sigm0 'SMZZ' 'SCAL' ) ;
def_00 = 'EXCO' def0 'EIXX' ;
def_0 = 'MAXI' def_00 ;
def1 = 'MAXI' ( 'EXCO' def0 'EIXX' ) ;
def2 = 'MAXI' ( 'EXCO' def0 'EIYY' ) ;
def3 = 'MAXI' ( 'EXCO' def0 'EIZZ' ) ;
def4 = 'MAXI' ( 'EXCO' def0 'GIXY' ) ;
def5 = 'MAXI' ( 'EXCO' def0 'GIXZ' ) ;
def6 = 'MAXI' ( 'EXCO' def0 'GIYZ' ) ;
defp1 = ( def1 * def1 ) + ( def2 * def2 ) +
( def3 * def3 ) ;
defp1 = defp1 - ( def1 * def2 ) - ( def2 * def3 ) -
( def1 * def3 ) ;
defp2 = ( def4 * def4 ) + ( def5 * def5 ) +
( def6 * def6 ) ;
defp0 = defp1 + ( 3. * defp2 ) ;
defp0 = ( defp0 ** .5 ) * 2. / 3. ;
sigx1 = sigx1 'ET' ( 'PROG' sigx0 ) ;
sigx2 = sigx2 'ET' ( 'PROG' sigx00 ) ;
depx1 = depx1 'ET' ( 'PROG' depx0 ) ;
depx2 = depx2 'ET' ( 'PROG' depx00 ) ;
sig_1 = sig_1 'ET' ( 'PROG' sig_0 ) ;
def_1 = def_1 'ET' ( 'PROG' def_0 ) ;
sig_3dy = sig_3dy 'ET' ( 'PROG' ( sig_y / sig_0 ) ) ;
sig_3dz = sig_3dz 'ET' ( 'PROG' ( sig_y / sig_0 ) ) ;
epst1 = epst1 'ET' ( 'PROG' epsx10 ) ;
*
* Densite RHO1
*
RHO1 = RHO0 / ( 1. + treps0 ) ;
eta = RHO1 / RHO0 ;
*
* Module de cisaillement G00
*
G00 = YOUNG1 / ( 2. * ( 1. + XNU1 ) ) ;
*
* Pulsation de Debye W0
*
W0 = ( G00 / RHO1 ) ** ( .5 ) ;
DTETA0 = ( 4. / 3.1416 ) ** ( .5 ) ;
DTETA0 = DTETA0 * W0 / 6. ;
DTETA0 = deps0 / DTETA0 ;
*
* Contrainte de saturation
*
'SI' ( ( 'ABS' dt0 ) < 1.E-10 ) ;
YS1 = SINF1 ;
'SINON' ;
YS1 = 'ERF' ( K1 * ( 'LOG' ( G1 / DTETA0 ) ) ) ;
YS1 = S01 - ( ( S01 - SINF1 ) * YS1 ) ;
'FINSI' ;
YS2 = S01 * ( ( DTETA0 / G1 ) ** ( BETA1 ) ) ;
YS0 = ( 'ABS' ( YS1 - YS2 ) ) + YS1 + YS2 ;
YS0 = YS0 / 2. ;
*
* Limite d'élasticité
*
'SI' ( ( 'ABS' dt0 ) < 1.E-10 ) ;
YL1 = YINF1 ;
'SINON' ;
YL1 = 'ERF' ( K1 * ( 'LOG' ( G1 / DTETA0 ) ) ) ;
YL1 = Y01 - ( ( Y01 - YINF1 ) * YL1 ) ;
'FINSI' ;
YL2 = Y11 * ( ( DTETA0 / G1 ) ** ( Y21 ) ) ;
YL3 = ( 'ABS' ( YL2 - YS2 ) ) - YL2 - YS2 ;
YL3 = -1. * YL3 / 2. ;
YL0 = ( 'ABS' ( YL1 - YL3 ) ) + YL1 + YL3 ;
YL0 = YL0 / 2. ;
*
'SI' ( sig_0 '>' ( YL0 * G00 ) ) ;
*
* Materiau C.C.
*
'SI' ( P11 'EGA' 0. ) ;
*
x0 = 0. ;
x2 = x0 ;
tr1 = treps0 - ( A1 * ( epsx10 - x2 ) /
( 3. * B1 ) ) ;
tr1 = tr1 / 3. ;
y2 = 'EXP' ( -1. * TAU1 * ( x2 - tr1 ) /
( YS0 - YL0 ) ) ;
y2 = YS0 - ( ( YS0 - YL0 ) * y2 ) ;
y2 = y2 * G00 ;
y2 = y2 + ( YOUNG1 * x2 ) ;
y2 = y2 - ( YOUNG1 * epsx10 ) ;
*
x1 = epsx10 ;
x2 = x1 ;
tr1 = treps0 - ( A1 * ( epsx10 - x2 ) /
( 3. * B1 ) ) ;
tr1 = tr1 / 3. ;
y2 = 'EXP' ( -1. * TAU1 * ( x2 - tr1 ) /
( YS0 - YL0 ) ) ;
y2 = YS0 - ( ( YS0 - YL0 ) * y2 ) ;
y2 = y2 * G00 ;
y2 = y2 + ( YOUNG1 * x2 ) ;
y2 = y2 - ( YOUNG1 * epsx10 ) ;
*
'REPETER' bloc2 ;
x2 = ( x1 + x0 ) / 2. ;
tr1 = treps0 - ( A1 * ( epsx10 - x2 ) /
( 3. * B1 ) ) ;
tr1 = tr1 / 3. ;
y2 = 'EXP' ( -1. * TAU1 * ( x2 - tr1 ) /
( YS0 - YL0 ) ) ;
y2 = YS0 - ( ( YS0 - YL0 ) * y2 ) ;
y2 = y2 * G00 ;
y2 = y2 + ( YOUNG1 * x2 ) ;
y2 = y2 - ( YOUNG1 * epsx10 ) ;
*
'SI' ( y2 > 1.E-5 ) ;
x1 = x2 ;
'SINON' ;
'SI' ( y2 < -1.E-5 ) ;
x0 = x2 ;
'SINON' ;
epsp0 = x2 ;
epsp1 = epsp1 'ET' ( 'PROG' epsp0 ) ;
den0 = A1 * GP0 * ( epsx10 - x2 ) / 3. ;
den0 = den0 / ( eta ** ( 1. / 3. ) ) ;
sup0 = A1 * ( G00 + GT0 ) *
( epsx10 - x2 ) ;
sig0 = sup0 / ( 1. + den0 ) ;
sig1 = sig1 'ET' ( 'PROG' sig0 ) ;
'QUITTER' bloc2 ;
'FINSI' ;
'FINSI' ;
'FIN' bloc2 ;
*
'SINON' ;
*
* autres materiaux
*
x0 = 0. ;
x2 = x0 ;
ex0 = P11 * ( YS0 - YL0 ) / ( S01 - YL0 ) ;
ex1 = ( S01 - YL0 ) * ( ( 'EXP' ex0 ) - 1. ) ;
tr1 = treps0 - ( A1 * ( epsx10 - x2 ) /
( 3. * B1 ) ) ;
tr1 = tr1 / 3. ;
y2 = 'EXP' ( -1. * P11 * TAU1 *
( x2 - tr1 ) / ex1 ) ;
y2 = ( 1. - ( 'EXP' ( -1. * ex0 ) ) ) * y2 ;
y2 = 'LOG' ( 1. - y2 ) ;
y2 = ( ( S01 - YL0 ) * y2 / P11 ) + YS0 ;
y2 = y2 * G00 ;
y2 = y2 + ( YOUNG1 * x2 ) ;
y2 = y2 - ( YOUNG1 * epsx10 ) ;
y0 = y2 ;
*
x1 = epsx10 ;
x2 = x1 ;
tr1 = treps0 - ( A1 * ( epsx10 - x2 ) /
( 3. * B1 ) ) ;
tr1 = tr1 / 3. ;
y2 = 'EXP' ( -1. * P11 * TAU1 *
( x2 - tr1 ) / ex1 ) ;
y2 = ( 1. - ( 'EXP' ( -1. * ex0 ) ) ) * y2 ;
y2 = 'LOG' ( 1. - y2 ) ;
y2 = ( ( S01 - YL0 ) * y2 / P11 ) + YS0 ;
y2 = y2 * G00 ;
y2 = y2 + ( YOUNG1 * x2 ) ;
y2 = y2 - ( YOUNG1 * epsx10 ) ;
y1 = y2 ;
*
'REPETER' bloc2 ;
x2 = ( x0 + x1 ) / 2. ;
tr1 = treps0 - ( A1 * ( epsx10 - x2 ) /
( 3. * B1 ) ) ;
tr1 = tr1 / 3. ;
y2 = 'EXP' ( -1. * P11 * TAU1 *
( x2 - tr1 ) / ex1 ) ;
y2 = ( 1. - ( 'EXP' ( -1. * ex0 ) ) ) * y2 ;
y2 = 'LOG' ( 1. - y2 ) ;
y2 = ( ( S01 - YL0 ) * y2 / P11 ) + YS0 ;
y2 = y2 * G00 ;
y2 = y2 + ( YOUNG1 * x2 ) ;
y2 = y2 - ( YOUNG1 * epsx10 ) ;
*
'SI' ( y2 > ( 1.E-8 * ( 'ABS' ( y1 - y0 ))));
x1 = x2 ;
'SINON' ;
'SI' (y2 < ( -1.E-8 * ('ABS'( y0 - y1 ))));
x0 = x2 ;
'SINON' ;
epsp0 = x2 ;
epsp1 = epsp1 'ET' ( 'PROG' epsp0 ) ;
den0 = A1 * GP0 * ( epsx10 - x2 ) / 3. ;
den0 = den0 / ( eta ** ( 1. / 3. ) ) ;
sup0 = A1 * ( G00 + GT0 ) *
( epsx10 - x2 ) ;
sig0 = sup0 / ( 1. + den0 ) ;
sig1 = sig1 'ET' ( 'PROG' sig0 ) ;
'QUITTER' bloc2 ;
'FINSI' ;
'FINSI' ;
'FIN' bloc2 ;
'FINSI' ;
*
'SINON' ;
epsp0 = 0. ;
epsp1 = epsp1 'ET' ( 'PROG' epsp0 ) ;
sig0 = sig_0 ;
sig1 = sig1 'ET' ( 'PROG' sig0 ) ;
'FINSI' ;
*
err_s0 = 'ABS' ( sig0 - sig_0 ) ;
err_s0 = err_s0 / sig0 ;
err_s0 = err_s0 * 100. ;
err1 = err1 'ET' ( 'PROG' err_s0 ) ;
err_e0 = 'ABS' ( epsp0 - def_0 ) ;
'SI' (def_0 '>' ( 1.E-1 * eps_el0 ) ) ;
err_e0 = err_e0 / def_0 ;
'SINON' ;
err_e0 = 0. ;
'FINSI' ;
err_e0 = err_e0 * 100. ;
'SI' ( err_e0 '>' 5.E-2 ) ;
'ERRE' 5 ;
'FINSI' ;
'SI' ( err_s0 '>' 5.E-2 ) ;
'ERRE' 5 ;
'FINSI' ;
err2 = err2 'ET' ( 'PROG' err_e0 ) ;
*
'FIN' bloc1 ;
*
*
'FIN' ;
Test preston1 Comments
MOD0 = MODE VOL1 MECANIQUE ELASTIQUE ISOTROPE
PLASTIQUE PRESTON ;
MAT0 = MATE MOD0 YOUN 2.1E11 NU 0.3
RHO 7.8E3 TAU 0.025
P 0. S0 0.0085 SINF 0.00055
K 0. G 0.00001
Y0 0.0001 YINF 0.0001 Y1 0.094 Y2 0.575
BETA 0.25 GP 3.00 GT 0. MU 1.97
TMO 1220. ;
Preston, Tonks and Wallace propose a mathematical
formulation of the Von Mises's yielding stress based
on the theory of the dislocations and the dimensional
analysis. The constitutive equations of the model are:
