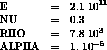
Test name
zeril1
Calculation type
ISOTROPIC ELASTOPLASTIC MECHANICS
Finite element type
CUB8
Topic
Zerilli-Armstrong model
The structure is a beam embedded at the lower and
at the upper surface. It is subjected to tensile
strength (imposed displacements) at the end. The
beam follows an elastoplastic law according to the
Zerilli-Armstrong's model.
Goal
Test the Zerilli-Armstrong model for BCC structure.
Version
97' customer version
Model description
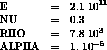
* Test Zeril.dgibi: Jeux de données *
* --------------------------------- *
* *
**************************************************
* *
* TEST DE VALIDATION D'UNE LOI DE COMPORTEMENT *
* -------------------------------------------- *
* DE MATERIAU *
* ----------- *
* *
* LOI DE COMPORTEMENT DE: *
* ZERILLI-ARMSTRONG *
* CAS CUBIQUE CENTRE ( C.C. ) *
* *
* MAILLAGE: *
* UNE BARRE DE SECTION CARREE *
* LONGUEUR L=.5 M *
* LARGEUR l=.01 M *
* *
* CHARGEMENT: *
* ESSAI DE TRACTION *
* DEPLACEMENTS IMPOSES *
* *
**************************************************
*
*
*
opti echo 0 dime 3 elem cub8 ;
*
*
* Maillage
*
l1 = .5 ;
l2 = .01 ;
l3 = .01 ;
n1 = 50 ;
n2 = 1 ;
n3 = 1 ;
p1 = 0. 0. 0. ;
p2 = l1 0. 0. ;
p3 = l1 l2 0. ;
p4 = 0. l2 0. ;
p5 = 0. 0. l3 ;
p6 = l1 0. l3 ;
p7 = l1 l2 l3 ;
p8 = 0. l2 l3 ;
d1 = d p1 n3 p5 ;
d2 = d p5 n2 p8 ;
d3 = d p8 n3 p4 ;
d4 = d p4 n2 p1 ;
sur1 = 'DALL' d1 d2 d3 d4 ;
d5 = d p2 n3 p6 ;
d6 = d p6 n2 p7 ;
d7 = d p7 n3 p3 ;
d8 = d p3 n2 p2 ;
sur2 = 'DALL' d5 d6 d7 d8 ;
vol1 = sur1 'VOLU' n1 sur2 ;
*
* Modele de calcul
*
mod0 = 'MODE' vol1 'MECANIQUE' 'ELASTIQUE' 'ISOTROPE'
'PLASTIQUE' 'ZERILLI' ;
mat0 = 'MATE' mod0 'YOUN' 2.1E11 'NU' 0.3
'RHO' 7.8E3 'ALPHA' 1.E-5 'DYG' 46.5E6
'C1' 1033.E6 'C2' 890.E6 'C3' (300. * 698.E-5)
'C4' ( 300. * 415.E-6 ) 'C5' 266.E6
'N' 0.289 'K' 6.957E5 'L' 1E-3 'TYPE' 1. ;
*
* Conditions aux limites
*
cl1 = 'BLOQ' sur1 'UX' ;
cl2 = 'BLOQ' sur2 'UX' ;
cl3 = 'BLOQ' p1 'UX' 'UY' 'UZ' ;
cl4 = 'BLOQ' p5 'UX' 'UY' ;
cl0 = cl1 'ET' cl2 'ET' cl3 'ET' cl4 ;
*
* Chargement
*
dep1 = 'DEPI' cl2 .1 ;
ev0 = 'EVOL' 'MANU' temps ( 'PROG' 0. .01 ) y
( 'PROG' 0. 1. ) ;
cha0 = 'CHAR' 'DIMP' dep1 ev0 ;
*
* Temps du calcul
*
dt0 = .00005 ;
tfin0 = .0005 ;
*
*
* Resolution par PASAPAS
*---------------------------------------
*
ta1 = 'TABLE' ;
ta1 .'MODELE' = mod0 ;
ta1 .'CARACTERISTIQUES' = mat0 ;
ta1 .'BLOCAGES_MECANIQUES' = cl0 ;
ta1 .'CHARGEMENT' = cha0 ;
ta1 .'TEMPS_CALCULES' = 'PROG' 0. 'PAS' dt0 tfin0 ;
*
PASAPAS ta1 ;
*
* Post-traitement
*-----------------------------------------
*
dim0 = 'DIME' ta1 .'TEMPS' - 1 ;
YOUNG0 = 'EXCO' mat0 'YOUNG' 'SCAL' ;
YOUNG1 = 'MAXI' YOUNG0 ;
DYG0 = 'EXCO' mat0 'DYG' 'SCAL' ;
DYG1 = 'MAXI' DYG0 ;
C1 = 'EXCO' mat0 'C1' 'SCAL' ;
C11 = 'MAXI' C1 ;
C2 = 'EXCO' mat0 'C2' 'SCAL' ;
C21 = 'MAXI' C2 ;
C3 = 'EXCO' mat0 'C3' 'SCAL' ;
C31 = 'MAXI' C3 ;
C4 = 'EXCO' mat0 'C4' 'SCAL' ;
C41 = 'MAXI' C4 ;
C5 = 'EXCO' mat0 'C5' 'SCAL' ;
C51 = 'MAXI' C5 ;
XK0 = 'EXCO' mat0 'K' 'SCAL' ;
XK1 = 'MAXI' XK0 ;
XL0 = 'EXCO' mat0 'L' 'SCAL' ;
XL1 = 'MAXI' XL0 ;
XN0 = 'EXCO' mat0 'N' 'SCAL' ;
XN1 = 'MAXI' XN0 ;
TYPE0 = 'EXCO' mat0 'TYPE' 'SCAL' ;
TYPE1 = 'MAXI' TYPE0 ;
eps_el0 = ( DYG1 + ( XK1 * ( XL1 ** (-.5) ) ) ) /
YOUNG1 ;
err_e1 = 0. ;
err_s1 = 0. ;
'REPETER' bloc1 dim0 ;
i1 = &bloc1 ;
depl1 = 'EXCO' ta1 .'DEPLACEMENTS'.i1 'UX' 'SCAL' ;
depl0 = 'EXCO' ta1 .'DEPLACEMENTS'.(i1 - 1 ) 'UX'
'SCAL' ;
dep1 = 'MAXI' depl1 ;
eps1 = dep1 / l1 ;
dep0 = 'MAXI' depl0 ;
sigm0 = ta1 .'CONTRAINTES'.i1 ;
depeq0 = ta1 .'VARIABLES_INTERNES'.i1 ;
def0 = ta1 .'DEFORMATIONS_INELASTIQUES'.i1 ;
t1 = ta1 .'TEMPS'.i1 ;
t0 = ta1 .'TEMPS'.(i1 - 1) ;
dt0 = t1 - t0 ;
dt0 = 0. ;
'SI' ( ( 'ABS' dt0 ) < 1.E-10 ) ;
deps0 = 0. ;
'SINON' ;
deps0 = ( dep1 - dep0 ) / ( dt0 * l1 ) ;
'FINSI' ;
*
sigx0 = 'MAXI' ( 'VMIS' mod0 sigm0 ) ;
sigx00 = 'MINI' ( 'VMIS' mod0 sigm0 ) ;
depx0 = 'MAXI' depeq0 ;
depx00 = 'MINI' depeq0 ;
sig_00 = 'EXCO' sigm0 'SMXX' 'SCAL' ;
sig_0 = 'MAXI' sig_00 ;
sig_y = 'MAXI' ( 'EXCO' sigm0 'SMYY' 'SCAL' ) ;
sig_z = 'MAXI' ( 'EXCO' sigm0 'SMZZ' 'SCAL' ) ;
def_00 = 'EXCO' def0 'EIXX' ;
def_0 = 'MAXI' def_00 ;
*
* Materiau cfc
*
'SI' ( TYPE1 'EGA' 0. ) ;
*
'SI' ( sigx0 '>EG'
( DYG1 + ( XK1 * ( XL1 ** (-.5) ) ) ) ) ;
'SI' ( ( 'ABS' deps0 ) < 1.E-10 ) ;
B0 = 0. ;
'SINON' ;
B0 = C21 * ( EXP ( ( C41 * ( LOG deps0 ) )
- C31 ) ) ;
'FINSI' ;
A0 = YOUNG1 ;
C0 = DYG1 + ( XK1 * ( XL1 ** (-.5) ) )
- ( YOUNG1 * eps1 ) ;
*
DELTA = ( B0 * B0 ) - ( 4. * A0 * C0 ) ;
X1 = ( -1. * B0 - ( ( DELTA ) ** ( 0.5) ) ) /
( 2. * A0 ) ;
X2 = ( -1. * B0 + ( ( DELTA ) ** ( 0.5) ) ) /
( 2. * A0 ) ;
epsp0 = X2 * X2 ;
sig0 = YOUNG1 * ( eps1 - epsp0 ) ;
*
'SINON' ;
epsp0 = 0. ;
sig0 = sig_0 ;
'FINSI' ;
*
'SINON' ;
*
* materiau CC
*
LIM0 = DYG1 + ( XK1 * ( XL1 ** (-.5) ) ) ;
'SI' ( ( 'ABS' deps0 ) < 1.E-10 ) ;
LIM0 = LIM0 + 0. ;
'SINON' ;
LIM0 = LIM0 +
( C11 * ( EXP ( ( C41 * ( LOG deps0 ) )
- C31 ) ) ) ;
'FINSI' ;
'SI' ( sig_0 > LIM0 ) ;
A0 = YOUNG1 ;
'SI' ( ( 'ABS' deps0 ) < 1.E-10 ) ;
B0 = 0. ;
'SINON' ;
B0 = C11 * ( EXP ( ( C41 * ( LOG deps0 ) )
- C31 ) ) ;
'FINSI' ;
B0 = B0 + DYG1 + ( XK1 * ( XL1 ** (-.5) ) )
- ( YOUNG1 * eps1 ) ;
C0 = C51 ;
*
x0 = 0. ;
x2 = x0 ;
y2 = A0 * x2 ;
y2 = y2 + ( C0 * ( x2 ** XN1 ) ) ;
y2 = y2 + B0 ;
*
x1 = eps1 ;
x2 = x1 ;
y2 = A0 * x2 ;
y2 = y2 + ( C0 * ( x2 ** XN1 ) ) ;
y2 = y2 + B0 ;
*
'REPETER' bloc2 ;
*
x2 = ( x0 + x1 ) / 2. ;
y2 = A0 * x2 ;
y2 = y2 + ( C0 * ( x2 ** XN1 ) ) ;
y2 = y2 + B0 ;
*
'SI' ( y2 > 1.E-5 ) ;
x1 = x2 ;
'SINON' ;
'SI' ( y2 < -1.E-5 ) ;
x0 = x2 ;
'SINON' ;
epsp0 = x2 ;
sig0 = YOUNG1 * ( eps1 - x2 ) ;
'QUITTER' bloc2 ;
'FINSI' ;
'FINSI' ;
*
'FIN' bloc2 ;
*
'SINON' ;
epsp0 = 0. ;
sig0 = sig_0 ;
'FINSI' ;
*
'FINSI' ;
*
err_s0 = 'ABS' ( sig0 - sig_0 ) ;
err_s0 = err_s0 / sig0 ;
err_s0 = err_s0 * 100. ;
err_e0 = 'ABS' ( epsp0 - def_0 ) ;
'SI' (def_0 '>' ( 1.E-1 * eps_el0 ) ) ;
err_e0 = err_e0 / def_0 ;
'SINON' ;
err_e0 = 0. ;
'FINSI' ;
err_e0 = err_e0 * 100. ;
*
* Erreur trop grande ?
*
'SI' ( err_e0 > 1. ) ;
'ERRE' 5 ;
err_e1 = 100. ;
'SINON' ;
err_e1 = err_e1 + 0. ;
'FINSI' ;
'SI' ( err_s0 > 1. ) ;
'ERRE' 5 ;
err_s1 = 100. ;
'SINON' ;
err_s1 = err_s1 + 0. ;
'FINSI' ;
*
'FIN' bloc1 ;
*
'SI' ( ( err_e1 < 1. ) 'ET' ( err_s1 < 1. ) ) ;
'ERRE' 0 ;
'FINSI' ;
*
*
'FIN' ;
Test zeril1 Comments
MOD0 = MODE VOL1 MECANIQUE ELASTIQUE ISOTROPE
PLASTIQUE ZERILLI ;
MAT0 = MATE MOD0 YOUN 2.1E11 NU 0.3
RHO 7.8E3 ALPHA 1.E-5 DYG 46.5E6
C1 1033.E6 C2 890.E6 C3 (300. * 698.E-5)
C4 ( 300. * 415.E-6 ) C5 266.E6
N 0.289 K 6.957E5 L 1E-3 TYPE 1. ;
The Zerilli-Armstrong model proposes a mathematical
formulation of the Von Mises's yielding stress
based on the theory of dislocations. The constitutive
equations of this model are as follow: