Test name
plas1
Calculation type
MECHANICS PLASTICITY 2D PLANE STRESS
Finite element type
COQ4
Topic
A rectangular-plate subjected to simple bending.
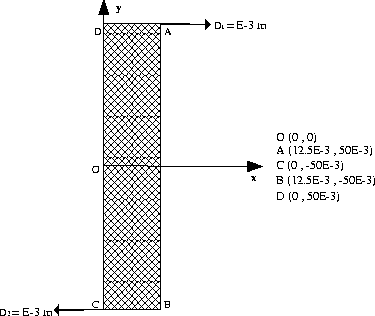
The structure is a rectangular-plate subjected to a simple bending. This bending is
obtained by the fixed displacement (D) at the tips (see figure), wich is a function of
time (T).
At the first step of time (0.02875), the strain range is elastic, at the second
one (0.05), it is plastic. At both time steps, the
elastic and the plastic theoretical bending moments are compared to the
CASTEM computed values. These values are computed from the reactions.
Goal
Find the computed elastic and plastic bending moment M1 and M2. The theoreticals values
are :
M1 = 805 kN M2 = 1074 kN
Reference CASTEM
Test NAFEMS : Analytical-Solution : MP1 Modélisation des structures élastiques dans CASTEM 2000.
Version
97' customer version
Model description

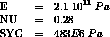
Test plas1 Results
RESULTS

CASTEM FIGURES
* Test Plas1.dgibi: Jeux de données *
* --------------------------------- *
* *
* CAS TEST DU 91/10/24 PROVENANCE : MILL
* CAS TEST DU 91/10/15 PROVENANCE : STRU
OPTION ECHO 0;
GRAPH='N';
SAUT PAGE ;
*
*******************************************************
* TEST PLAS1
*
* Sortie du domaine élastique et phase plastique
* (comportement élasto-plastique parfait)
*
* Une plaque rectangulaire est soumise à une flexion
* pure. La flexion est imposée par le déplacement des
* extrémités de la plaque (voir schéma ci-dessous) en
* fonction du temps.
*
* Au premier pas de temps (0.02875) on se trouve dans
* le domaine élastique et au deuxième pas de temps
* (0.05) on se trouve dans le domaine plastique. Au
* deux pas de temps, les moments fléchissants calculés
* à partir des forces de réaction sont comparés avec
* les résultats théoriques.
*
*******************************************************
*
* D .____. A ----> D1
* | |
* | |
* .____. A1
* | |
* | |
* .____. A2
* | |
* | |
* .____. A3
* | |
* | |
* O .____. A4
* | |
* | |
* .____. A5
* | |
* | |
* .____. A6
* | |
* | |
* .____. A7
* | |
* | |
* C .____. B <---- D2
*
*------------------------------------------------------
* LES POINTS A1 A A7 SERVIRONT A FAIRE VARIER LE
* DEPLACEMENT IMPOSE LINEAIREMANT DE A (D1) A B (D2)
*------------------------------------------------------
*
*******************************************************
TITRE 'PLAQUE RECTANGULAIRE EN FLEXION PURE' ;
OPTION ECHO 1 ;
OPTION DIME 2 ELEM QUA4 MODE PLAN CONT ;
TEMPS ;
*
*-------------- D{finition de la g{om{trie ------------
*
O = 0 0 ;
A = 12.5E-3 50E-3 ;
B = 12.5E-3 -50E-3 ;
C = 0 -50E-3 ;
D = 0 50E-3 ;
*
A1 = 12.5E-3 37.5E-3 ;
A2 = 12.5E-3 25E-3 ;
A3 = 12.5E-3 12.5E-3 ;
A4 = 12.5E-3 0 ;
A5 = 12.5E-3 -12.5E-3 ;
A6 = 12.5E-3 -25E-3 ;
A7 = 12.5E-3 -37.5E-3 ;
*
L1 = A DROIT 1 A1 ;
L2 = A1 DROIT 1 A2 ;
L3 = A2 DROIT 1 A3 ;
L4 = A3 DROIT 1 A4 ;
L5 = A4 DROIT 1 A5 ;
L6 = A5 DROIT 1 A6 ;
L7 = A6 DROIT 1 A7 ;
L8 = A7 DROIT 1 B ;
*
L14 = L1 ET L2 ET L3 ET L4 ET L5 ET L6 ET L7 ET L8 ;
*
L9 = B DROIT 1 C ;
L10 = C DROIT 4 O ;
L11 = O DROIT 4 D ;
L12 = L10 ET L11 ;
L13 = D DROIT 1 A ;
*
SU = L14 L9 L12 L13 DALL PLAN ;
ELIM 0.01 SU ;
SI(NEG GRAPH 'N');
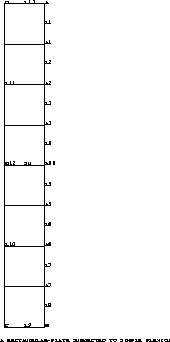
TRACE SU ;
FINSI;
*
*------- Définition des conditions aux limites --------
*----------- et des déplacements imposés --------------
*
CL1 = BLOQ L12 UX ;
CL1B = BLOQ O UY ;
CL2 = BLOQ A UX ;
CL3 = BLOQ B UX ;
CL = CL1 ET CL1B ET CL2 ET CL3 ;
*
D1 = DEPI CL2 1E-3 ;
D2 = DEPI CL3 -1E-3 ;
DEP = D1 ET D2 ;
*
*--------------------------------------
* Exemple : EN A1 , D = 7/8 D1 + 1/8 D2
*--------------------------------------
*
*--------- Les déplacements en chaque noeud -----------
*----------- est une relation linéaire des ------------
*------------ d{éplacements des extrémités ------------
*------- Création de la rigidité correspondante -------
*
R1 = RELA 8 UX A1 - 7 UX A - 1 UX B ;
R2 = RELA 8 UX A2 - 6 UX A - 2 UX B ;
R3 = RELA 8 UX A3 - 5 UX A - 3 UX B ;
R4 = RELA 8 UX A4 - 4 UX A - 4 UX B ;
R5 = RELA 8 UX A5 - 3 UX A - 5 UX B ;
R6 = RELA 8 UX A6 - 2 UX A - 6 UX B ;
R7 = RELA 8 UX A7 - 1 UX A - 7 UX B ;
R = R1 ET R2 ET R3 ET R4 ET R5 ET R6 ET R7 ;
*
*-------- Utilisation de l'opérateur NONLIN -----------
*-- Les objets utilisés par la procédure NONLIN sont --
*------- définis dans les lignes qui suivent ----------
*
MO= MODL SU MECANIQUE ELASTIQUE PLASTIQUE PARFAIT QUA4;
*
*----- Définition du matériau et de la rigidité -------
*----------- SIGY est la limite élastique -------------
*
MAT1 = MATR MO YOUN 2.1E11 SIGY 483E6 NU 0.3 ;
RI1 = RIGI MO MAT1 ;
RIG1 = RI1 ET CL ET R ;
*
*------- Création d'une relation linéaire entre -------
*------------- le déplacement et le temps -------------
*
LI1 = PROG 0. 1. ;
LI2 = PROG 0. 1. ;
EV = EVOL MANU T LI1 F(T) LI2 ;
*
* Remarque : au temps T, le d{placement vaut F(T)*D .
*----------------------------------------------------
*
CHA1 = CHAR 'DIMP' DEP EV ;
*
*------- Création de la liste des pas de calcul -------
*----- 0.02875 est le dernier incrément élastique -----
*- 0.05 est un incrément plastique (calcul analytique)
*
LIS1 = PROG 0.02875 0.05 ;
*
*----------- Calcul par l'op{rateur NONLIN ------------
*
TAB1 = TABLE ;
TAB1.'BLOCAGES_MECANIQUES' = CL 'ET' R;
TAB1.'MODELE' = MO;
TAB1.'CHARGEMENT' = CHA1;
TAB1.'CARACTERISTIQUES' = MAT1;
TAB1.'TEMPS_CALCULES' = LIS1;
PASAPAS TAB1 ;
*
*--------- calcul et impression des résultats ---------
*
REA1 = REAC RIG1 (TAB1.DEPLACEMENTS.1) ;
REA2 = REAC RIG1 (TAB1.DEPLACEMENTS.2) ;
*
R11 = EXTR REA1 FX A ;
R21 = EXTR REA2 FX A ;
R12 = EXTR REA1 FX A1 ;
R22 = EXTR REA2 FX A1 ;
R13 = EXTR REA1 FX A2 ;
R23 = EXTR REA2 FX A2 ;
R14 = EXTR REA1 FX A3 ;
R24 = EXTR REA2 FX A3 ;
*
* Pour obtenir les moments fléchissants, les réactions
* - obtenues sont multipliées par leur bras de levier -
*
M1 = (2.E-3)*((0.050*R11)+(0.0375*R12)+(0.025*R13)
+(0.0125*R14)) ;
M2 = (2.E-3)*((0.050*R21)+(0.0375*R22)+(0.025*R23)
+(0.0125*R24)) ;
*
SAUT PAGE ; SAUT 2 LIGN ;
*
MESS ' MOMENT THEORIQUE
MOMENT CALCULE';
SAUT 1 LIGN ;
MESS 'INCREMENT ELASTIQUE M1= 805 KN
M1= 'M1 'KN';
SAUT 1 LIGN ;
MESS 'INCREMENT PLASTIQUE M2= 1074 KN
M2= 'M2 'KN';
*
TEMPS ;
* CODE FONCTIONNEMENT
MR1=805. ;
MR2=1074. ;
RESI1=ABS((M1-MR1)/MR1);
RESI2=ABS((M2-MR2)/MR2);
SI((RESI1 <EG 5E-2) ET (RESI2 <EG 5E-2));
ERRE 0;
SINO;
ERRE 5;
FINSI;
FIN ;
Test plas1 Comments
CL1 = BLOQ L12 UX ; CL1B = BLOQ O UY ; CL2 = BLOQ A UX ; CL3 = BLOQ B UX ; CL = CL1 ET CL1B ET CL2 ET CL3 ;The BLOQUE operator constructs the RIGIDITE stiffness, which is associated to conditions of imposed values on the unknowns of a discretized problem. Later, this stiffness will have to be added to that of the structure.
D1 = DEPI CL2 1E-3 ; D2 = DEPI CL3 -1E-3 ; DEP = D1 ET D2 ;Thus, The DEPI operator specifies the value of certain relationships. CL2 and CL3 are the RIGIDITE, type object, of BLOCAGE subtype, defining the conditions imposed on the degrees of freedom . Here 1E-3 and -1E-3 , are the values to be imposed on certain displacement relations.
R1 = RELA 8 UX A1 - 7 UX A - 1 UX B ; R2 = RELA 8 UX A2 - 6 UX A - 2 UX B ; R3 = RELA 8 UX A3 - 5 UX A - 3 UX B ; R4 = RELA 8 UX A4 - 4 UX A - 4 UX B ; R5 = RELA 8 UX A5 - 3 UX A - 5 UX B ; R6 = RELA 8 UX A6 - 2 UX A - 6 UX B ; R7 = RELA 8 UX A7 - 1 UX A - 7 UX B ; R = R1 ET R2 ET R3 ET R4 ET R5 ET R6 ET R7 ;The RELATION operator enables the user to construct the stiffness associated with a linear relation between the unknowns named Ui, weighted by (possible) coefficients, for respective mesh nodes (here it is UX A1, UX B , UX A2, UX B,.......). The DEPIMP operator allows the user to impose a non-zero value on the relation. For example here at a point A1 the displacement D is :
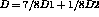
TAB1 = TABLE ; TAB1.'BLOCAGES_MECANIQUES' = CL 'ET' R; TAB1.'MODELE' = MO; TAB1.'CHARGEMENT' = CHA1; TAB1.'CARACTERISTIQUES' = MAT1; TAB1.'TEMPS_CALCULES' = LIS1; PASAPAS TAB1 ;The (NONLIN) PASAPAS procedure enables the user to carry out an incremental non linear calculation. The non linearity can result either from the material (plasticity) or from the large displacements, or else from both. Here the non linearity resut from the material.
REA1 = REAC RIG1 (TAB1.DEPLACEMENTS.1) ; REA2 = REAC RIG1 (TAB1.DEPLACEMENTS.2) ;The reaction operator REAC constructs the reaction force from the solution field TAB1.DEPLACEMENT.1 and TAB1.DEPLACEMENTS.2, of CHPOINT types, resulting from a linear system on the first member of which conditions have been imposed. allowing the verification of these conditions.
M1 = (2.E-3)*((0.050*R11)+(0.0375*R12)+(0.025*R13)+(0.0125*R14)) ; M2 = (2.E-3)*((0.050*R21)+(0.0375*R22)+(0.025*R23)+(0.0125*R24)) ;