Equation de la chaleur

Cette équation modélise les transferts thermiques par conduction et s'écrit

$$\rho c_p \frac{\partial T}{\partial t} = div ( \lambda \vec{\nabla} T)$$

où $T$ désigne la température (en $K$) ; $\rho$ la densité (en $kg/m^3$) ; $c_p$ la chaleur spécifique à pression constante (en $J/kg/K$) ; $\lambda$ la conductivité thermique (en $W/m/K$).

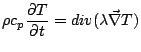
En supposant que les propriétés matérielles sont indépendantes du temps et de l'espace et que le matériau est isotrope, l'équation de la chaleur s'écrit

$$\frac{\partial T}{\partial t} = \alpha \Delta T$$

où $\alpha = \lambda / (\rho c_p)$ désigne la diffusivité thermique (en $m^2/s$).

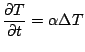
Pour pouvoir résoudre ce problème, on doit connaître le champ de température à l'instant initial ainsi que l'évolution au cours du temps de la température (ou de son flux) à la frontière du domaine -- le problème est elliptique en espace et parabolique en temps.

Si on s'intéresse au régime permanent, $T$ est solution de

$$\Delta T = 0$$

Le problème est alors bien posé à condition de connaître les valeurs de la température (ou de son flux) à la frontière du domaine à l'état stationnaire -- caractéristique d'un problème elliptique en espace. Si le flux est imposé sur l'ensemble de la frontière la solution est connue à une constante près. En instationnaire par contre, si le flux est imposé sur l'ensemble de la frontière la solution est parfaitement connue, les conditions initiales fixant la valeur de la constante.