*
*-------------------------------------------------------------------------------
* Convection/Diffusion : CAS SMITH ET HUTTON
* REFERENCE : NUMERICAL HEAT TRANSFER, VOL.5, p.439, 1982
*-------------------------------------------------------------------------------
* Les faces latérales et supérieure d'une boite rectangulaire sont
* imperméables. Le fluide rentre et sort de la boite par la face
* inférieure. Il rentre par la moitié gauche de la face inférieure
* et sort par la moitié droite de cette même face.
*
* Le champ de vitesse est connu et donné par :
* v(x,y) = 2y(1-x2) i - 2x(1-y2) j
* la taille de la boite étant [-1,1]x[0,1]
*
* L'écoulement transporte un scalaire passif qui est injecté en entrée
* suivant le profil :
* c(x,0) = 1 + tanh(10(2x+1))
* avec x variant de -1 à 0 (entrée du domaine).
* Sur les frontières imperméables du domaine, la concentration est
* constante et égale à 1-tanh(10).
*
* On cherche la solution stationnaire du transport par diffusion et
* convection du champ scalaire passif. On compare la solution en sortie
* avec la solution de référence. Plusieurs solutions sont calculées
* suivant le Peclet (rapport entre la convection et la diffusion).
*-------------------------------------------------------------------------------
*
'OPTI' 'DIME' 2 'ISOV' 'SULI' ;
*
* Pe : Peclet (convection sur diffusion)
* Les cas traités dans la référence sont 10, 100, 500, 1000 et 1000000
Pe = 10 ;
*
* KSUPG : Option de décentrement (CENTREE/SUPG/SUPGDC)
* GRAPH : Booleen pour l'affichage des tracés à l'issue du calcul
* POST1 : Booleen pour affichage Résidu à chaque pas
* POST2 : Booleen pour affichage C(x,t) à chaque pas
* COMPLET : Booleen modifiant la finesse du maillage et la précision des calculs
* NX : Nombre de maille suivant x
* NY : Nombre de maille suivant y
* nbiter : Nombre de pas de temps
* tolera : Tolérance pour la comparaison avec la solution de référence
KSUPG = 'SUPG' ;
GRAPH = VRAI ;
POST1 = FAUX ;
POST2 = 'NON' POST1 ;
COMPLET = FAUX ;
'SI' ( COMPLET ) ;
'OPTI' 'ELEM' 'TRI3' ;
NY = 20 ;
NX = 2 * NY ;
nbiter = 2000 ;
tolera = 0.006 ;
'SINON' ;
'OPTI' 'ELEM' 'QUA4' ;
NY = 10 ;
NX = 2 * NY ;
nbiter = 100 ;
tolera = 0.012 ;
'FINSI' ;
*
*==================================================================
* Calcul du résidu en température et arrêt suivant un critère
*==================================================================
* E/ : RVX : TABLE : TABLE des données créées par EQEX
* ARG1 : Fréquence d'impression
* ARG2 : Critère d'arrêt
* /S : MAT1 : MATRIK : Objet vide
* /S : CHP1 : CHPO : Objet vide
*------------------------------------------------------------------
*
'DEBPROC' residu rvx*table ;
RV = rvx . 'EQEX' ;
FREQ = RVX . 'ARG1' ;
EPS0 = RVX . 'ARG2' ;
NITER = RV . 'NITER' ;
DD = RV . 'PASDETPS' . 'NUPASDT' ;
NN = DD '/' FREQ ;
L0 = 'EGA' (DD '-' (FREQ*NN)) 0 ;
'SI' L0 ;
RANG0 = RV . 'PASDETPS' . 'NUPASDT' ;
TIME0 = RV . 'PASDETPS' . 'TPS' ;
CN0 = RV . 'INCO' . 'CN' ;
CNM0 = RV . 'INCO' . 'CN2' ;
ERR0 = ('MAXIMUM' ('ABS' (CN0 '-' CNM0))) '+' 1.D-20 ;
ERR10 = ('LOG' ERR0 ) '/' ('LOG' 10.) ;
'MESSAGE' 'Résidu en Température au pas'
RANG0 '(' TIME0 ') :' ERR0 ':' ERR10 ;
RV . 'INCO' . 'IT' = RV . 'INCO' . 'IT' 'ET' ('PROG' RANG0) ;
RV . 'INCO' . 'TI' = RV . 'INCO' . 'TI' 'ET' ('PROG' TIME0) ;
RV . 'INCO' . 'ER' = RV . 'INCO' . 'ER' 'ET' ('PROG' ERR10) ;
EV1 = 'EVOL' 'MANUEL' (RV . 'INCO' . 'IT') (RV . 'INCO' . 'ER') ;
Y1 = ('LOG' EPS0) '/' ('LOG' 10) ;
'SI' POST1 ;
X1 = 0. ; X2 = RV . 'ITMA' ;
'DESSIN' EV1 'YBOR' Y1 0. 'NCLK'
'TITR' 'Evolution du résidu' ;
'FINSI' ;
'SI' POST2 ;
L1 = (PROG 0. PAS 100. 2000.)* 1.D-3 ;
trace L1 cn0 DOMTOT CNT1 'TITR' 'Concentration' 'NCLK' ;
'FINSI' ;
'SI' ((ERR10 < Y1) 'ET' (DD > 10)) ;
RV . 'TFINAL' = RV . 'PASDETPS' . 'TPS' ;
'FINSI' ;
'FINSI' ;
RV . 'INCO' . 'CN2' = 'COPIER' RV . 'INCO' . 'CN' ;
mat1 chp1 = 'KOPS' 'MATRIK' ;
'FINP' mat1 chp1 ;
*------------------------------------------------------------------
*
*
*- MAILLAGE
*
*
* Points
A1 = -1.0 0.0 ;
A2 = 1.0 0.0 ;
A3 = 1.0 1.0 ;
A4 = -1.0 1.0 ;
A0 = 0.0 0.0 ;
*
* Lignes
LIN = A1 'DROI' NY A0 ;
LOUT = A0 'DROI' NY A2 ;
FBAS = LIN 'ET' LOUT ;
FDRO = A2 'DROI' NY A3 ;
FHAU = A3 'DROI' NX A4 ;
FGAU = A4 'DROI' NY A1 ;
LIMP = FDRO 'ET' FHAU 'ET' FGAU ;
*
* Maillage
DOMTOT = 'DALL' FBAS FDRO FHAU FGAU 'PLAN' ;
CNT1 = 'CONT' DOMTOT ;
*
* Modèles et sous-modèles
DOM2 = 'CHAN' 'QUAF' DOMTOT ;
LIN2 = 'CHAN' 'QUAF' LIN ;
LIMP2 = 'CHAN' 'QUAF' LIMP ;
$DOMTOT = 'MODE' DOM2 'NAVIER_STOKES' 'LINE' ;
$LIN = 'MODE' LIN2 'NAVIER_STOKES' 'LINE' ;
$LIMP = 'MODE' LIMP2 'NAVIER_STOKES' 'LINE' ;
*
* Récupération des maillages et fusion des supports
DOMTOT = 'DOMA' $DOMTOT 'MAILLAGE' ;
LIN = 'DOMA' $LIN 'MAILLAGE' ;
LIMP = 'DOMA' $LIMP 'MAILLAGE' ;
FDOMTOT = 'DOMA' $DOMTOT 'FACE' ;
CLIN = 'DOMA' $LIN 'CENTRE' ;
CLIMP = 'DOMA' $LIMP 'CENTRE' ;
'ELIM' FDOMTOT (CLIN 'ET' CLIMP) 1.D-3 ;
*
* Champ de vitesse
XX YY = 'COOR' DOMTOT ;
VXSH = (2.*YY)*(1.0-(XX*XX)) ;
VYSH = (-2.*XX)*(1.0-(YY*YY)) ;
VX0 = 'NOMC' 'UX' VXSH ;
VY0 = 'NOMC' 'UY' VYSH ;
VX = 'KCHT' $DOMTOT 'SCAL' 'SOMMET' 'COMP' 'UX' VX0 ;
VY = 'KCHT' $DOMTOT 'SCAL' 'SOMMET' 'COMP' 'UY' VY0 ;
CHVIT = 'KCHT' $DOMTOT 'VECT' 'SOMMET' 'COMP' 'UX' 'UY' (VX 'ET' VY) ;
*
* Diffusion (1/Pe)
DIF = 1.0 / ('FLOT' Pe) ;
*
* Profil de concentration à l'entrée
XBAS = 'COOR' 1 LIN ;
TOTO = 2.0*XBAS + 1.0 * 10. ;
SOLUTION = 'TANH' TOTO ;
SOLUTION = 1.0 + SOLUTION ;
CHP1 = 'KCHT' $LIN 'SCAL' 'SOMMET' 0. SOLUTION ;
CHP1 = 'NOMC' 'CN' CHP1 ;
*
* Conditions aux limites en concentration sur les frontières imperméables
C1 = (1.0 - (TANH 10.0)) ;
*
* Description du problème de transport
RV1 = 'EQEX' $DOMTOT 'ITMA' nbiter 'ALFA' 0.7
'ZONE' $DOMTOT 'OPER' residu 1 1.D-7
'OPTI' KSUPG 'EFM1' 'EXPL'
'ZONE' $DOMTOT 'OPER' 'TSCAL' DIF 'VITESSE' 0. 'INCO' 'CN'
'OPTI' 'CENTREE'
'ZONE' $DOMTOT 'OPER' 'DFDT' 1. 'CN' 'DELTAT' 'INCO' 'CN' ;
*
* Description des conditions aux limites
RV1 = 'EQEX' RV1
'CLIM' 'CN' 'TIMP' LIN CHP1
'CLIM' 'CN' 'TIMP' LIMP C1 ;
*
* Description des conditions initiales
RV1 . 'INCO' = TABLE 'INCO' ;
RV1 . 'INCO' . 'CN' = 'KCHT' $DOMTOT 'SCAL' 'SOMMET' 0. ;
*
* Autres data
RV1 . 'INCO' . 'VITESSE' = CHVIT ;
RV1 . 'INCO' . 'CN2' = 'KCHT' $DOMTOT 'SCAL' 'SOMMET' 0. ;
RV1 . 'INCO' . 'IT' = 'PROG' ;
RV1 . 'INCO' . 'TI' = 'PROG' ;
RV1 . 'INCO' . 'ER' = 'PROG' ;
*
*
*- CALCUL
*
*
EXEC RV1 ;
*
*
*- ANALYSE DES RESULTATS
*
*
EVOL1 = 'EVOL' 'CHPO' (RV1 . 'INCO' . 'CN') 'SCAL' FBAS ;
EVOL2 = 'EVOL' 'CHPO' XX 'SCAL' FBAS ;
LIX = 'EXTR' EVOL2 'ORDO' ;
LIU = 'EXTR' EVOL1 'ORDO' ;
EVOL3 = 'EVOL' 'MANU' 'X' LIX 'C(X,0)' LIU ;
*
* Solutions de référence
LIXT = PROG 0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 ;
SI ( Pe 'EGA' 10 ) ;
LIUT = PROG 1.989 1.402 1.146 0.946 0.775 0.621 0.480 0.349
0.227 0.111 0.000 ;
FINSI ;
SI ( Pe 'EGA' 100 ) ;
LIUT = PROG 2.000 1.940 1.836 1.627 1.288 0.869 0.480 0.209
0.070 0.017 0.000 ;
FINSI ;
SI ( Pe 'EGA' 500 ) ;
LIUT = PROG 2.000 2.000 1.998 1.965 1.702 0.947 0.242 0.023
0.001 0.000 0.000 ;
FINSI ;
SI ( Pe 'EGA' 1000 ) ;
LIUT = PROG 2.000 2.000 2.000 1.985 1.841 0.951 0.154 0.001
0.000 0.000 0.000 ;
FINSI ;
SI ( Pe 'EGA' 1000000 ) ;
LIUT = PROG 2.000 2.000 2.000 1.999 1.964 1.000 0.036 0.001
0.000 0.000 0.000 ;
FINSI ;
EVOL4 = EVOL 'MANU' 'X' LIXT 'Uref(X,0)' LIUT ;
LIUC = IPOL LIXT LIX LIU ;
NP = DIME LIXT ;
ERR0 = 0. ;
REPETER BLOC1 NP ;
UCAL = EXTRAIRE LIUC &BLOC1 ;
UREF = EXTRAIRE LIUT &BLOC1 ;
ERR0 = ERR0 + ((UCAL-UREF)*(UCAL-UREF)) ;
FIN BLOC1 ;
ERR0 = ERR0/NP ;
ERR0 = ERR0 '**' 0.5 ;
MESSAGE 'ERREUR ' ERR0 ;
SI ( ERR0 > tolera ) ;
* ERREUR 5 ;
FINSI ;
*
*
*- POST-TRAITEMENT
*
*
'SI' GRAPH ;
*
* Maillage
'TRAC' DOMTOT 'TITR' 'Maillage' ;
*
* Vitesse
UNCH = 'VECT' CHVIT 0.1 'UX' 'UY' 'ROUGE' ;
'TRAC' UNCH DOMTOT CNT1 'TITR' 'Vitesse transportante' ;
*
* Concentration
'TRAC' DOMTOT (RV1 . 'INCO' . 'CN') CNT1 'TITR' 'Concentration' ;
*
* Convergence vers la solution stationnaire
EV1 = 'EVOL' 'MANU' 'ITERATIONS' (RV1 . 'INCO' . 'IT')
'LOG|E|inf' (RV1 . 'INCO' . 'ER') ;
'DESS' EV1 'XBOR' 0. ('FLOT' NBITER) 'YBOR' -20.0 0.0
'TITR' 'Evolution du résidu' ;
*
* Comparaison avec la solution analytique
TAB1 = TABLE ;
TAB1 . TITRE = TABLE ;
TAB1. TITRE . 1 = 'MOT' 'CAST3M' ;
TAB1. TITRE . 2 = 'MOT' 'REFERENCE' ;
TAB1. 2 = 'MARQ LOSA NOLI' ;
'TITR' 'Comparaison CAST3M/Référence' ;
'DESS' (EVOL3 ET EVOL4) 'LEGE' TAB1
'MIMA' 'XBOR' -1.0 1.0 'YBOR' -1.0 3.0 ;
*
FINSI ;
*FIN ;

|

|
|
Fig 13 - Maillage 40x20 constitué de triangles et champ de vitesse
pour le cas-test de Smith et Hutton
|
|

|
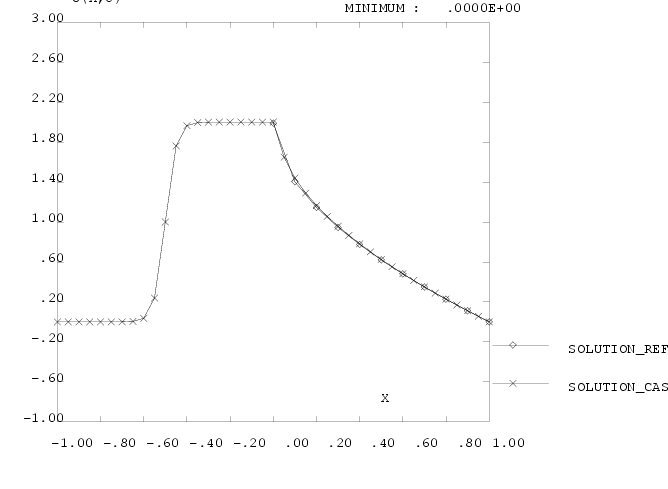
|
Fig 14 - Cas 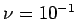 , TSCAL option SUPG , TSCAL option SUPG
|
|

|
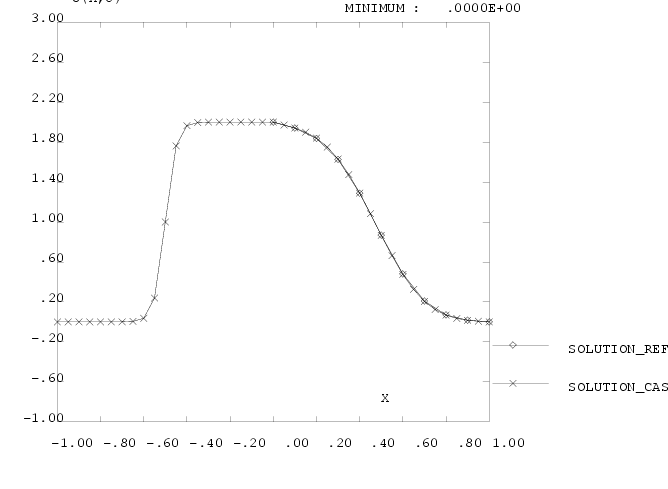
|
Fig 14 - Cas 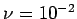 , TSCAL option SUPG , TSCAL option SUPG
|
|

|
|
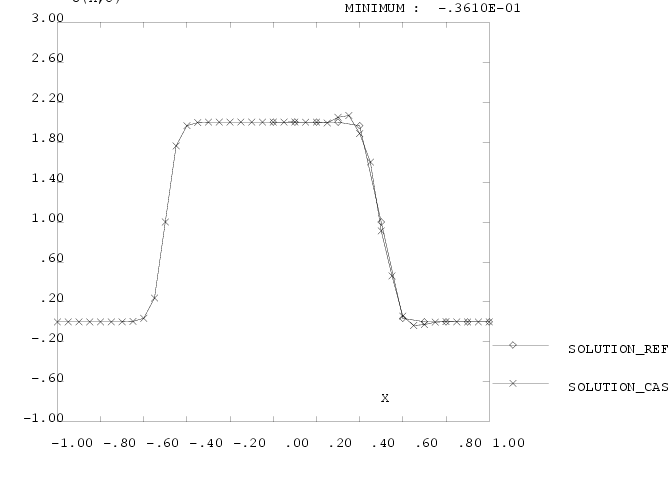
Fig 14 - Cas 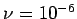 , TSCAL option SUPG , TSCAL option SUPG
|
|

|
|
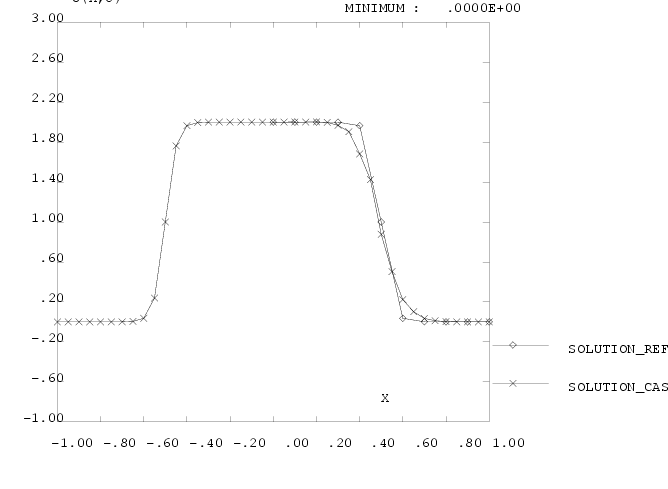
Fig 14 - Cas 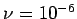 , TSCAL option SUPG-CC , TSCAL option SUPG-CC
|




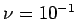 , TSCAL option SUPG
, TSCAL option SUPG


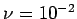 , TSCAL option SUPG
, TSCAL option SUPG


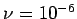 , TSCAL option SUPG
, TSCAL option SUPG


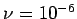 , TSCAL option SUPG-CC
, TSCAL option SUPG-CC