Test name
vibr2
Calculation type
MECHANICS DYNAMICS 2D AXISYMMETRICAL
Finite element type
QUA8
Topic
Uniform radial mode shapes of a thick sphere.
Eigen frequencies and shapes of a thick sphere are calculated. Only the uniform radial vibration shapes are studied.
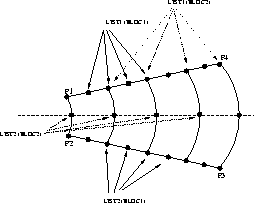
Only a sector of the sphere is meshed and computation is done with axisymmetrical mode.
Boundary conditions corresponding to this meshing are obtained by using the operator RELA : nodes of similar radius have similar displacements.
Goal
Find the eigen frequencies of the sphere.
Reference
Test NAFEMS number fv42.
Version
97' customer version
Model description

Test vibr2 Results
Results

CASTEM figures
* Test Vibr2.dgibi: Jeux de données *
* --------------------------------- *
* *
* CAS TEST DU 91/06/13 PROVENANCE : TEST
SAUT PAGE;
*
*******************************************************
* *
* TEST VIBR2 *
* *
* SPHERE EPAISSE : VIBRATION RADIALE UNIFORME *
* *
* Test NAFEMS , test numero fv42 *
* *
* On se propose de calculer les frequences et *
* modes propres d'une sphere epaisse. On ne s'inte- *
* resse qu'aux modes de vibration radiale uniforme. *
* *
* On ne maille qu'un secteur de la sphere et l'on *
* travaille en mode axisymetrique. *
* *
* Pour obtenir les conditions aux limites corres- *
* pondantes, on utilise l'operateur RELA (les noeuds *
* ayant le meme rayon ont le meme deplacement radial)*
* *
*******************************************************
*
OPTI ECHO 1;
*
OPTI DIME 2;
OPTI MODE AXIS;
OPTI ELEM QUA8;
*
GRAPH = 'N';
*-----------------------------------------------------*
* geometrie - maillage *
*-----------------------------------------------------*
*
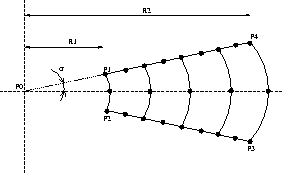
ALPHA = 5.; COSALPHA = COS ALPHA; SINALPHA = SIN ALPHA;
*
P0 = 0. 0.;
P1 = 1.8 ( 1.8 * SINALPHA);
P2 = 1.8 (-1.8 * SINALPHA);
P3 = 6.0 (-6.0 * SINALPHA);
P4 = 6.0 ( 6.0 * SINALPHA);
*
D23 = P2 DROI 5 P3;
*
SUR1 = D23 ROTA 1 (2 * ALPHA) P0;
D41 = COTE 3 SUR1;
*
ELIM (SUR1 ET D23 ET D41) 0.001;
*
SI (NEG GRAPH 'N');
TITR 'VIBR2 : MAILLAGE';
TRAC QUAL SUR1;
FINSI;
*
*-----------------------------------------------------*
* modl - materiau - rigidite - masse *
*-----------------------------------------------------*
*
MOD1 = MODL SUR1 MECANIQUE QUA8;
MAT1 = MATR MOD1 YOUN 2.E11 NU 0.3 RHO 8E3;
RIG1 = RIGI MOD1 MAT1;
MAS1 = MASS MOD1 MAT1;
*
*-----------------------------------------------------*
* conditions aux limites *
*-----------------------------------------------------*
DIR1 = (-1 * SINALPHA) (-1 * COSALPHA);
DIR2 = (-1 * SINALPHA) COSALPHA;
*
CL1 = BLOQ DEPL DIRECTION DIR1 D23;
CL2 = BLOQ DEPL DIRECTION DIR2 D41;
CLI1 = CL1 ET CL2;
*
DIR3 = COSALPHA (-1 * SINALPHA);
DIR4 = COSALPHA SINALPHA;
*
LIST1 = LECT 27 22 17 23 18 24 19 25 20 26 21;
LIST2 = LECT 1 6 2 7 3 8 4 9 5 10 11;
*
I = 0;
REPETER BLOC1 11;
I = I + 1;
J = EXTR LIST1 I;
K = EXTR LIST2 I;
CL3 = RELA 1 DEPL DIRECTION DIR4 (NOEUD J)
- 1 DEPL DIRECTION DIR3 (NOEUD K);
CLI1 = CLI1 ET CL3;
FIN BLOC1;
*
LIST1 = LECT 27 17 18 19 20 21;
LIST2 = LECT 28 12 13 14 15 16;
*
I = 0;
REPETER BLOC2 6;
I = I + 1;
J = EXTR LIST1 I;
K = EXTR LIST2 I;
CL4 = RELA 1 DEPL DIRECTION DIR4 (NOEUD J)
- 1 UR (NOEUD K);
CLI1 = CLI1 ET CL4;
FIN BLOC2;
*
RIG1 = RIG1 ET CLI1;
*
*-----------------------------------------------------*
* calcul des frequences propres *
*-----------------------------------------------------*
*
* Utilisation de l'operateur VIBR.
*
FRE1 = TABLE;
FRE1.1 = 369.91;
FRE1.2 = 838.03;
FRE1.3 = 1451.2;
FRE1.4 = 2117.0;
FRE1.5 = 2795.8;
*
LIST1 = PROG FRE1.1 FRE1.2 FRE1.3 FRE1.4 FRE1.5;
*
RESUL = VIBR PROC LIST1 RIG1 MAS1;
*
*-----------------------------------------------------*
* extraction des resultats
*-----------------------------------------------------*
*
MESS ' RESULTATS FV42.DGIBI';
MESS ' --------------------';
SAUT 2 LIGN;
MESS ' SPHERE EN VIBRATION RADIALE';
SAUT 2 LIGN;
*
FRE2 = TABLE; ERG = TABLE;
DEP = TABLE; DEF = TABLE; EVO = TABLE;
*
I = 0;
REPETER BLOC3 5;
*
I = I + 1;
FRE2.I = TIRE RESUL FREQ RANG I;
ERG.I = 100 * (ABS ((FRE1.I - FRE2.I) / FRE1.I));
MESS ' MODE ' I;
MESS ' ----------';
MESS ' Frequence propre theorique :' FRE1.I 'Hz';
MESS ' Frequence propre calculee :' FRE2.I 'Hz';
MESS ' Soit un ecart de : ' ERG.I '%';
SAUT 1 LIGN;
*
* Trace facultatif des modes propres
*
SI (NEG GRAPH 'N');
DEP.I = TIRE RESUL DEPL RANG I;
DEF0 = DEFO SUR1 DEP.I 0. ROUGE;
DEF.I = DEFO SUR1 DEP.I VERT;
TITR ' Mode propre : Deplacement radial';
TRAC (DEF0 ET DEF.I);
EVO.I = EVOL VERT CHPO DEP.I UR D23;
DESSIN EVO.I;
FINSI;
*
FIN BLOC3;
*
*-----------------------------------------------------*
* code fonctionnement *
*-----------------------------------------------------*
*
ERGMAX = MAXI (PROG ERG.1 ERG.2 ERG.3 ERG.4 ERG.5);
*
SAUT 2 LIGN;
SI (ERGMAX <EG 5.);
ERRE 0;
SINON;
ERRE 5;
FINSI;
*
SAUT 2 LIGN;
TEMPS;
SAUT 2 LIGN;
*
FIN;
*
Test vibr2 Comments
Only the radial vibrations are studied, so the normal displacements are constrained : DIR1 is the normal to D23 and DIR2 to D41.
Nodes of similar radius have similar radial displacements : this condition is given in loops BLOC1 and BLOC2. The different lists of integers correspond to the numbers of nodes (display the number of nodes when drawing the meshing). The loop BLOC1 is relative to nodes on D41 and D23. The loop BLOC2 is relative to nodes on D41 and middle nodes.