Test name
elas8
Calculation type
MECHANICS ELASTICITY 2D PLANE STRESS
Finite element type
QUA8
Topic
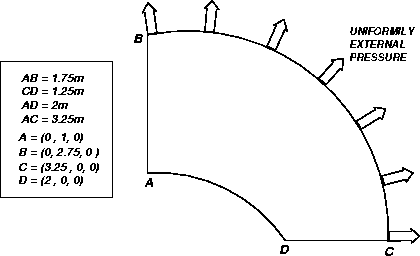
solid : ELLIPTICAL MEMBRANE SUBJECTED TO LINEAR LOAD.
The model is an elliptical membrane, obtained by a projection of one arc of circle onto one plane. This structure is subjected to linear load in one sides. On grounds of symmetry, we solve this problem in axisymmetrical mode.
Goal
Find the stress at a point D(2, 0; 0). The analytical value is Smyy = 92.7 MPa.
Reference CASTEM
Test NAFEMS : ME12 : Modélisation des structures élastiques dans CASTEM 2000.
Version
97' customer releas
Model description

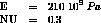
Test elas8 Results
RESULTS
CASTEM figures
* Test Elas8.dgibi: Jeux de données * * --------------------------------- * * * CAS TEST DU 91/06/13 PROVENANCE : TEST SAUT PAGE; * ******************************************************* * * * TEST ELAS8 * * * * MEMBRANE ELLIPTIQUE (Contraintes planes) * * * * cas-test NAFEMS : test numero LE1 * * * * * * Une membrane elliptique obtenue par projection * * d'arcs de cercles sur un plan, est soumis a une * * force lineique sur l'un de ces cotes. * * * * Vue les symetries le probleme est traite en * * contraintes planes. * * * * On se propose de calculer la contrainte smyy * * au point D. * * * ******************************************************* * OPTI ECHO 0; * OPTI DIME 3; OPTI ELEM QUA8; * GRAPH = 'N'; * *=====================================================* * geometrie : maillage * *=====================================================* * * Dimension en metres * * Points * PB = 0. 2.75 0.; PB1 = 0. 2.75 (((3.25 ** 2) - (2.75 ** 2)) ** 0.5); PC = 3.25 0. 0.; * C1 = PC CERC 6 (0. 0. 0.) PB1; C2 = C1 PROJ CYLI (0. 0. 1) PLAN (0 0 0) (1 0 0) (0 1 0); * PA = 0. 1. 0.; PA1 = 0. 1. (((2. ** 2) - (1. ** 2)) ** 0.5); PD = 2. 0. 0.; * C3 = PD CERC 6 (0. 0. 0.) PA1; C4 = C3 PROJ CYLI (0. 0. 1) PLAN (0 0 0) (1 0 0) (0 1 0); * D1 = PA DROI 2 (0. 1.583 0.) DROI 2 PB; D3 = PC DROI 2 (2.417 0. 0.) DROI 2 PD; * ELIM (D1 ET C2 ET D3 ET C4) 0.0001; SUR1 = DALL D1 C2 D3 C4 PLAN; * SI (NEG GRAPH 'N'); TITR 'ELAS8 : MAILLAGE'; TRAC (0 0 1000) QUAL SUR1; FINSI; * OPTI DIME 2; OPTI MODE PLAN CONT; * *=====================================================* * modele - affecte - materiau - caracteristique * * rigidite - conditions aux limites * *=====================================================* * MODL1 = MODL SUR1 MECANIQUE ELASTIQUE ISOTROPE QUA8; MATR1 = MATR MODL1 YOUN 210E9 NU 0.3; RI1 = RIGI MODL1 MATR1; * * Conditions aux limites * - droite d1: symetrie par rapport a l'axe des ordo. * - droite d2: symetrie par rapport a l'axe des absc. * CL1 = SYMT DEPL ROTA (0 0) (0 1) SUR1 0.0001; CL2 = SYMT DEPL ROTA (0 0) (1 0) SUR1 0.0001; * RIG1 = RI1 ET CL1 ET CL2; * *=====================================================* * Chargement * *=====================================================* * * Pression externe uniforme de 10e6Pa. * CHA1 = PRES MASS MODL1 -10.E6 C2; * *=====================================================* * resolution : champs de deplacements * *=====================================================* * DEP1 = RESO RIG1 CHA1; * * Trace facultatif de la deformee et des reactions * SI (NEG GRAPH 'N'); AMPVEC = 1.E-7; REA1 = REAC DEP1 RIG1; VECT1 = VECT CHA1 AMPVEC FX FY ROUGE; VECT2 = VECT REA1 AMPVEC FX FY BLEU; DEF0 = DEFO 0. DEP1 SUR1; DEF1 = DEFO 150. DEP1 SUR1 (VECT1 ET VECT2) VERT; TITR 'ELAS8 : DEFORMEE, CHARGEMENT, REACTIONS'; TRAC SUR1 (DEF0 ET DEF1); FINSI; * *=====================================================* * champs de contraintes * *=====================================================* * CHAM1 = SIGM MODL1 MATR1 DEP1; * * Interpolation aux noeuds du maillage * CHAM2 = CHAN NOEUD CHAM1 MODL1; CHP2 = CHAN CHPO CHAM2 MODL1; * *=====================================================* * extraction et affichage d'une contrainte * *=====================================================* * * On cherche la contrainte smyy a point D. * SMYYD = EXTR CHP2 SMYY PD;SMYYD = SMYYD / 1.E6; * SMYYD1 = 92.7; ERG = 100 * (ABS ((SMYYD - SMYYD1) / SMYYD1)); * MESS ' RESULTATS '; MESS ' --------- '; SAUT 1 LIGN; MESS ' CONTRAINTE SMYY THEORIQUE AU POINT D :' SMYYD1 'MPA'; MESS ' CONTRAINTE SMYY CALCULEE AU POINT D :' SMYYD 'MPA'; MESS ' SOIT UN ECART DE :' ERG '%'; SAUT 1 LIGN; * NBNOSUR1 = NBNO SUR1; NBELSUR1 = NBEL SUR1; MESS ' NOMBRE D ELEMENTS :' NBELSUR1 'QUA8'; MESS ' NOMBRE DE NOEUDS ;' NBNOSUR1 ; SAUT 1 LIGN; * *=====================================================* * code fonctionnement * *=====================================================* * SI (ERG <EG 5.); ERRE 0; SINON; ERRE 5; FINSI; * SAUT 1 LIGN; TEMPS; SAUT 1 LIGN; * FIN;
Test elas8 Comments
C4 = C3 PROJ CYLI (0. 0. 1) PLAN (0 0 0) (1 0 0) (0 1 0);
The operator PROJ(ETER) constructs the object C4 which results from the projection of the object C3 with respect of the vector (0. 0. 1.). The projection is done onto a plane support defined by 3 points (keyword PLAN followed by 3 points).
CL1 = SYMT DEPL ROTA (0 0) (0 1) SUR1 0.0001;
CL2 = SYMT DEPL ROTA (0 0) (1 0) SUR1 0.0001;
The operator SYMT imposes boundary conditions of symmetry type on the degrees of freedom in rotation (keyword ROTA). The two points define the axis of symmetry, SUR1 is the geometry on which are imposed the conditions and the real 0.0001 is the criterion of selection of the points.
CHA1 = PRES MASS MODL1 -10.E6 C2;
The operator PRES calculates the nodal forces equivalent to the pressure applied on the model object MODL1. The keyword MASS indicates that the type of the elements are massive (QUA4).