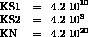
Test name
joi45
Calculation type
ORTHOTROPIC ELASTIC MECHANICS
Finite element type
QUA4, JOI4
Topic
Calculation of the thermal stresses on a 3D joint.
The structure is a parallelepipedic joint embedded from the lower
surface. The upper surface is free. The joint is subjected to a
shear load applied on the whole circumference of the upper surface
in the direction O-P1.
Goal
Calculate the displacements in the direction of the load, the
deformations, the stresses and the nodal force field resulting
from a stress field integration.
Version
97' customer version
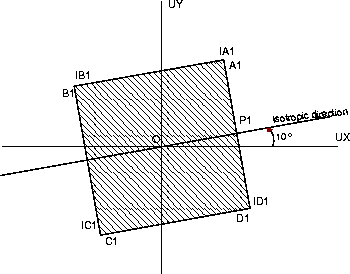
Model description
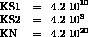
Angle (OX,OP1) = 55 degrees
O-P1 axis : first orthotropic direction
Test joi45 Results
RESULTS
Analytical solution:
F
delta = --------
K * A
where
F is the total load on the upper surface in the
direction OP1
K is the stiffness in the first orthotropic
direction
A is the surface of the joint
Projection of the solution in the axis X and Y:
deltax = delta * cos(55)
deltay = delta * sin(55)
Numerical application:
F = 100000
K = 4.2 E20
A = 4.0
deltax = 3.416 E-7
deltay = 4.875 E-7
* Test Joi45.dgibi: Jeux de données *
* --------------------------------- *
* *
OPTI ECHO 0 ;
SAUT PAGE ;
*=====================================================*
* *
* TEST JOI45 *
* *
* ESSAI DE CISAILLEMENT SUR UN JOINT 3 *
* ORTHOTROPE *
* *
* Un joint 3D JOI4 a sa surface inferieure *
* encastree. Sa surface superieure est libre. *
* Un effort de cisaillement est exerce sur le *
* pourtour de sa surface superieure, suivant la *
* direction O-P1. *
* *
* Y ! *
* .!. *
* . ! . *
* . ! . P1 *
* . ! / . *
* . ! / . *
* . ! / . *
* . O ! / . *
* ------------------------------------- X *
* . ! . *
* . ! . *
* . ! . *
* . ! . *
* . ! . *
* . ! . *
* .!. *
* ! *
* *
* Angle (OX,OP1) = 55 degres *
* L axe OP1 definit la premiere direction *
* d orthotropie *
* *
* Calcul de la solution analytique : *
* *
* F *
* delta = ------------- *
* K * A *
* ou *
* *
* delta = deplacement suivant la direction *
* de la force *
* F = Force totale exercee sur la surface *
* superieure, suivant la direction OP1 *
* K = raideur dans la premiere direction *
* d orthotropie *
* A = surface du joint *
* *
* Projection de la solution suivant les axes X et Y : *
* *
* deltax = delta * cos(55) *
* *
* deltay = delta * sin(55) *
*=====================================================*
OPTION DIME 3 ;
OPTION ELEM QUA4 MODE TRID ;
*
OO = 00.00 0.00 0.00 ;
ON = 00.00 0.00 1.00 ;
AN = 10.00 ;
*
* -------- DEFINITION DU POINT P1 --------------
* ----- POUR LES DIRECTIONS D'ORTHOTROPIE ------
*
P1 = 0.707106781 0.707106781 0.00 ;
P1 = P1 TOUR AN OO ON ;
*
* ------ DEFINITION DE LA SURFACE BOT DU JOINT --------
*
A1 = 1.414213562 0.000000000 0.00 ;
B1 = 0.000000000 1.414213562 0.00 ;
C1 =-1.414213562 0.000000000 0.00 ;
D1 = 0.000000000 -1.414213562 0.00 ;
*
A1 = A1 TOUR AN OO ON ;
B1 = B1 TOUR AN OO ON ;
C1 = C1 TOUR AN OO ON ;
D1 = D1 TOUR AN OO ON ;
*
* ---------- MAILLAGE ----------
*
H1 = A1 DROIT 1 B1 ;
H2 = B1 DROIT 1 C1 ;
H3 = C1 DROIT 1 D1 ;
H4 = D1 DROIT 1 A1 ;
*
L1 = H1 ET H2 ET H3 ET H4 ;
S1 = SURF L1 PLAN ;
*
* ------- DEFINITION DE LA SURFACE TOP DU JOINT -------
*
IA1 = 1.414213562 0.000000000 0.00 ;
IB1 = 0.000000000 1.414213562 0.00 ;
IC1 =-1.414213562 0.000000000 0.00 ;
ID1 = 0.000000000 -1.414213562 0.00 ;
*
IA1 = IA1 TOUR AN OO ON ;
IB1 = IB1 TOUR AN OO ON ;
IC1 = IC1 TOUR AN OO ON ;
ID1 = ID1 TOUR AN OO ON ;
*
* ---------- MAILLAGE ----------
*
IH1 = IA1 DROIT 1 IB1 ;
IH2 = IB1 DROIT 1 IC1 ;
IH3 = IC1 DROIT 1 ID1 ;
IH4 = ID1 DROIT 1 IA1 ;
*
IL1 = IH1 ET IH2 ET IH3 ET IH4 ;
IS1 = SURF IL1 PLAN ;
*
* ---------- CREATION DU JOINT JOI4 ----------
*
OPTION ELEM LIA4 ;
VOL = LIAISON 0.00001 S1 IS1 ;
*
* -------- DEFINITION DES CONDITIONS LIMITES ----------
*
CL11 = BLOQ A1 UX ;
CL12 = BLOQ A1 UY ;
CL13 = BLOQ A1 UZ ;
CL1 = CL11 ET CL12 ET CL13 ;
*
CL21 = BLOQ B1 UX ;
CL22 = BLOQ B1 UY ;
CL23 = BLOQ B1 UZ ;
CL2 = CL21 ET CL22 ET CL23 ;
*
CL31 = BLOQ C1 UX ;
CL32 = BLOQ C1 UY ;
CL33 = BLOQ C1 UZ ;
CL3 = CL31 ET CL32 ET CL33 ;
*
CL41 = BLOQ D1 UX ;
CL42 = BLOQ D1 UY ;
CL43 = BLOQ D1 UZ ;
CL4 = CL41 ET CL42 ET CL43 ;
*
CL = CL1 ET CL2 ET CL3 ET CL4 ;
*
* ------- DEFINITION DU MODELE DU JOINT ---------
*
MOD1 = MODL VOL 'MECANIQUE' 'ELASTIQUE' 'ORTHOTROPE'
JOI4 ;
MA1 = MATR MOD1 'DIRECTION' P1 'PARALLELE' KS1 4.2E10
KS2 4.2E08
KN 4.2E20 ;
**********************************************
FLOT1 = 0.0 ;
P3 = 3.0 1.0 1.0 ;
***MA1 = MATR MOD1 'DIRECTION' P1 'INCLINE' FLOT1 P3
*** KS1 4.2E10 KS2 4.2E08 KN 4.2E20 ;
**********************************************
**MA1 = MATR MOD1 'RADIAL' P1 KS1 4.2E10 KS2 4.2E08 KN
* 4.2E20 ;
*
* ---------- MATRICE DE RIGIDITE ---------
*
RI1 = RIGI MOD1 MA1 ;
RI2 = RI1 ET CL ;
* ---------- FORCE DE TRACTION ---------
*
FO1 = FORCE ( 57358.00 81915.00 0.00 ) IL1 ;
*
* ---------- RESOLUTION ---------
*
RE = RESO RI2 FO1 ;
SAUT PAGE ;
MESS ' ' ;
MESS ' ' ;
MESS ' ' ;
MESS'!==============================================!';
MESS'! !';
MESS'! TEST JOI45 !';
MESS'! !';
MESS'! ESSAI DE CISAILLEMENT SUR UN JOINT 3D !';
MESS'! ORTHOTROPE !';
MESS'! !';
MESS'! Un joint 3D JOI4 a sa surface inferieure !';
MESS'! encastree. Sa surface superieure est libre. !';
MESS'! Un effort de cisaillement est exerce sur le !';
MESS'! pourtour de sa surface superieure, suivant !';
MESS'! la direction O-P1. !';
MESS'! !';
MESS'! Y ! !';
MESS'! .!. !';
MESS'! . ! . !';
MESS'! . ! . P1 !';
MESS'! . ! / . !';
MESS'! . ! / . !';
MESS'! . ! / . !';
MESS'! . O ! / . !';
MESS'! ------------------------------------- X !';
MESS'! . ! . !';
MESS'! . ! . !';
MESS'! . ! . !';
MESS'! . ! . !';
MESS'! . ! . !';
MESS'! . ! . !';
MESS'! .!. !';
MESS'! ! !';
MESS'! !';
MESS'! Angle (OX,OP1) = 55 degres !';
MESS'! L axe OP1 definit la premiere direction !';
MESS'! d orthotropie !';
MESS'! !';
MESS'! !';
MESS'! Calcul de la solution analytique : !';
MESS'! !';
MESS'! F !';
MESS'! delta = ------------- !';
MESS'! K * A !';
MESS'! ou !';
MESS'! !';
MESS'! delta = deplacement suivant la direction !';
MESS'! de la force !';
MESS'! F = Force totale exercee sur la surface !';
MESS'! superieure,suivant la direction OP1 !';
MESS'! K = raideur dans la premiere direction !';
MESS'! d orthotropie !';
MESS'! A = surface du joint !';
MESS'! !';
MESS'! Projection de la solution suivant !';
MESS'! les axes X et Y : !';
MESS'! !';
MESS'! deltax = delta * cos(55) !';
MESS'! !';
MESS'! deltay = delta * sin(55) !';
MESS'! !';
MESS'! Application numerique : !';
MESS'! !';
MESS'! F = 100000 !';
MESS'! K = 4.2E20 !';
MESS'! A = 4.0 !';
MESS'! !';
MESS'! deltax = 3.416E-7 !';
MESS'! deltay = 4.875E-7 !';
MESS'! !';
MESS'!==============================================!';
MESS ' ' ;
MESS ' ' ;
SAUT PAGE ;
MESS ' Solution Calculee :' ;
MESS ' ' ;
*
SOLAX=3.416E-7 ;
SOLAY=4.875E-7 ;
*
LIST RE ;
*
* ---------- CODE DE FONCTIONNEMENT ----------
*
DEPIAX = EXTR RE UX IA1 ;
RESI1 = ABS( (DEPIAX-SOLAX)/SOLAX ) ;
*
DEPIAY = EXTR RE UY IA1 ;
RESI2 = ABS( (DEPIAY-SOLAY)/SOLAY ) ;
*
SI ( (RESI1 <EG 1E-3 ) ET (RESI2 <EG 1E-3 ) ) ;
ERRE 0 ;
SINO;
ERRE 5 ;
FINSI ;
*
* ---------- CALCUL DES DEFORMATIONS ----------
*
EPS1 = EPSI MOD1 MA1 RE ;
LIST EPS1 ;
*
* ---------- CALCUL DES CONTRAINTES ----------
*
SIG1 = SIGMA MOD1 MA1 RE ;
LIST SIG1 ;
*
* ---------- CALCUL DE BSIGMA ----------
*
BSI1 = BSIGMA MOD1 SIG1 ;
LIST BSI1 ;
*
FIN ;
Test joi45 Comments
BSI1 = BSIGMA MOD1 SIG1 ;The BSIGMA operator calculates the nodal force field (BST1) resulting from a stress field (SIG1) integration.