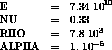
Test name
ohno2
Calculation type
ISOTROPIC VISCOPLASTIC MECHANICS - 2D AXIS
Finite element type
QUA8
Topic
Ohno -modified Chaboche-model for viscoplastic behaviour.
The structure is an axisymmetrical hollow cylinder
embedded at the lower surface. It is subjected to
imposed load at the upper surface: the radial strength
outwards. The cylinder follows Ohno's viscoplastic law
.
Goal
Test the Ohno's model for solid structures.
Version
97' customer version
Model description
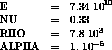
Test ohno2 Results
CASTEM FIGURES
* Test Ohno2.dgibi: Jeux de données *
* --------------------------------- *
* *
*
**************************************************
* *
* TEST DE VALIDATION D'UNE LOI DE COMPORTEMENT *
* -------------------------------------------- *
* DE MATERIAU *
* ----------- *
* *
* LOI DE COMPORTEMENT VISCOPLASTIQUE DE: *
* OHNO (CHABOCHE MODIFIE OHNO) *
* *
* TEST POUR DES ELEMENTS COQUE MINCE *
* ---------------------------------- *
* *
* MAILLAGES: *
* PREMIER MAILLAGE: ELEMENTS MASSIFS *
* DEUXIEME MAILLAGE: ELEMENTS COQUE MINCE *
* UN CYLINDRE CREUX AXISYMETRIQUE *
* LONGUEUR L =.1 M *
* RAYON INTERNE R =.05 M *
* EPAISSEUR E =.0005 M *
* *
* CHARGEMENT: *
* CYLINDRE ENCASTRE EN SON EXTREMITE BASSE *
* FORCES IMPOSEES SUR L'EXTREMITE DU HAUT: *
* FORCES RADIALES DIRIGEES VERS L'EXTERIEUR *
* *
**************************************************
*
opti echo 0 dime 2 elem qua8 mode axis ;
*
*
* Maillage
*
rayon0 = .05 ;
epais0 = .0005 ;
l1 = epais0 + rayon0 ;
l2 = .1 ;
n1 = 1 ;
n2 = 200 ;
p1 = rayon0 0. ;
p2 = l1 0. ;
p3 = l1 l2 ;
p4 = rayon0 l2 ;
d1 = d p1 n1 p2 ;
d2 = d p2 n2 p3 ;
d3 = d p3 n1 p4 ;
d4 = d p4 n2 p1 ;
vol1 = 'DALL' d1 d2 d3 d4 ;
*
* Modele de calcul
*
mod0 = 'MODE' vol1 'MECANIQUE' 'ELASTIQUE' 'ISOTROPE'
'VISCOPLASTIQUE' 'OHNO' ;
mat0 = 'MATE' mod0 'YOUN' 7.34E10 'NU' 0.33
'RHO' 7.8E3 'ALPHA' 1.E-5 'N' 24
'KK' 10.E6 'K0' 116.E6 'ALFK' 1.5 'ALFR' 0.35
'ALF' 2.E6 'A1' 67.5E6 'C1' 1300 'BET1' 4807.E6
'R1' 4 'A2' 80.E6 'C2' 45 'BET2' 58480.E6
'R2' 4 'PHI' 1. 'B' 12 'GAMA' 2.E-7 'M' 2
'QMAX' 455.E6 'QSTA' 200.E6 'MU' 19 'ETA' 0.06
'EXP1' 2. 'EXP2' 2. ;
*
* Conditions aux limites
*
cl1 = 'BLOQ' d1 'UR' 'UZ' 'RT' 'RZ' ;
cl0 = cl1 ;
*
* Chargement
*
pres0 = 1.E4 ;
p01 = ( rayon0 + ( epais0 / 2. ) ) l2 ;
p00 = vol1 'POIN' 'PROC' p01 ;
dep1 = 'FORCE' 'FR' pres0 p00 ;
ev0 = 'EVOL' 'MANU' temps ( 'PROG' 0. 10000. ) y
( 'PROG' 0. 1. ) ;
cha0 = 'CHAR' 'MECA' dep1 ev0 ;
vec1 = 'VECT' dep1 1.E-5 'FR' 'FZ' 'ROUG' ;
*
* Temps du calcul
*
dt0 = 20. ;
tfin0 = 700. ;
*
*
* Resolution par PASAPAS
*---------------------------------------
*
ta1 = 'TABLE' ;
ta1 .'MODELE' = mod0 ;
ta1 .'CARACTERISTIQUES' = mat0 ;
ta1 .'BLOCAGES_MECANIQUES' = cl0 ;
ta1 .'CHARGEMENT' = cha0 ;
ta1 .'TEMPS_CALCULES' = 'PROG' 0. 'PAS' dt0 tfin0 ;
*
PASAPAS ta1 ;
*
*
* Post-traitement
*-----------------------------------------
*
dim0 = 'DIME' ( ta1 .'TEMPS' ) ;
char2 = 'PROG' 0. ;
depl2 = 'PROG' 0. ;
defi2 = 'PROG' 0. ;
cont1 = 'PROG' 0. ;
*
reac0 = ta1 .'REACTIONS'.( dim0 - 1 ) ;
depl0 = ta1 .'DEPLACEMENTS'.( dim0 - 1 ) ;
vec2 = 'VECT' reac0 1.E-2 'FR' 'FZ' 'ROUG' ;
defo0 = 'DEFO' vol1 depl0 0. 'ROUG' ;
defo1 = 'DEFO' vol1 depl0 1. ;
reac1 = 'REDU' reac0 p1 ;
reac2 = 'REDU' reac0 p2 ;
vec01 = 'VECT' reac1 1.E-2 'FR' 'FZ' 'ROUG' ;
vec02 = 'VECT' reac2 1.E-2 'FR' 'FZ' 'VERT' ;
*
'REPETER' bloc0 ( dim0 - 1 ) ;
i0 = &bloc0 ;
reac0 = ta1 .'REACTIONS'.i0 ;
depl0 = ta1 .'DEPLACEMENTS'.i0 ;
sigm0 = ta1 .'CONTRAINTES'.i0 ;
defi0 = ta1 .'VARIABLES_INTERNES'.i0 ;
temp0 = ta1 .'TEMPS'.i0 ;
depl1 = 'EXTR' depl0 'UR' p3 ;
depl2 = depl2 'ET' ( 'PROG' depl1 ) ;
defi1 = 'MAXI' ( 'EXCO' defi0 'EPSE' ) ;
defi2 = defi2 'ET' ( 'PROG' defi1 ) ;
* cont0 = 'MAXI' ( 'EXCO' 'SMXX' sigm0 ) ;
* cont1 = cont1 'ET' ( 'PROG' cont0 ) ;
char1 = pres0 * temp0 / tfin0 ;
char2 = char2 'ET' ( 'PROG' char1 ) ;
'FIN' bloc0 ;
*
opti echo 0 dime 2 elem seg2 mode axis ;
*
*
* Maillage
*
epais0 = .0005 ;
rayon0 = .05 ;
l10 = .1 ;
n10 = 400 ;
p10 = rayon0 0. ;
p20 = rayon0 l10 ;
mail1 = d p10 n10 p20 ;
*
* Modele de calcul
*
mod00 = 'MODE' mail1 'MECANIQUE' 'ELASTIQUE' 'ISOTROPE'
'VISCOPLASTIQUE' 'OHNO' 'COQ2' ;
mat00 = 'MATE' mod00 'YOUN' 7.34E10 'NU' 0.33
'RHO' 7.8E3 'N' 24
'KK' 10.E6 'K0' 116.E6 'ALFK' 1.5 'ALFR' 0.35
'ALF' 2.E6 'A1' 67.5E6 'C1' 1300 'BET1' 4807.E6
'R1' 4 'A2' 80.E6 'C2' 45 'BET2' 58480.E6
'R2' 4 'PHI' 1. 'B' 12 'GAMA' 2.E-7 'M' 2
'QMAX' 455.E6 'QSTA' 200.E6 'MU' 19 'ETA' 0.06
'EXP1' 2. 'EXP2' 2. ;
car00 = 'CARA' mod00 'EPAI' epais0 'ALFA' ( 2. / 3. ) ;
*
* Conditions aux limites
*
cl10 = 'BLOQ' p10 'UR' 'UZ' 'RT' 'RZ' ;
cl00 = cl10 ;
*
* Chargement
*
pres0 = 1.E4 ;
dep10 = 'FORCE' 'FR' pres0 p20 ;
ev00 = 'EVOL' 'MANU' temps ( 'PROG' 0. 10000. ) y
( 'PROG' 0. 1. ) ;
cha00 = 'CHAR' 'MECA' dep10 ev00 ;
vec1 = 'VECT' dep10 1.E-5 'FR' 'FZ' ;
*
* Temps du calcul
*
dt00 = 20. ;
tfin00 = 700. ;
*
*
* Resolution par PASAPAS
*---------------------------------------
*
ta10 = 'TABLE' ;
ta10 .'MODELE' = mod00 ;
ta10 .'CARACTERISTIQUES' = mat00 'ET' car00 ;
ta10 .'BLOCAGES_MECANIQUES' = cl00 ;
ta10 .'CHARGEMENT' = cha00 ;
ta10 .'TEMPS_CALCULES' = 'PROG' 0. 'PAS' dt00 tfin00 ;
*
PASAPAS ta10 ;
*
*
* Post-traitement
*-----------------------------------------
*
dim10 = 'DIME' ta10 .'TEMPS' ;
depl12 = 'PROG' 0. ;
*
reac0 = ta10 .'REACTIONS'.( dim10 - 1 ) ;
depl0 = ta10 .'DEPLACEMENTS'.( dim10 - 1 ) ;
vec2 = 'VECT' reac0 1.E-2 'FR' 'FZ' 'ROUG' ;
defo0 = 'DEFO' mail1 depl0 0. ;
defo1 = 'DEFO' mail1 depl0 100. ;
*
'REPETER' bloc0 ( dim10 - 1 ) ;
i10 = &bloc0 ;
depl10 = ta10 .'DEPLACEMENTS'.i10 ;
temp10 = ta10 .'TEMPS'.i10 ;
depl11 = 'EXTR' depl10 'UR' p20 ;
depl12 = depl12 'ET' ( 'PROG' depl11 ) ;
'FIN' bloc0 ;
*
* Erreur
*
prob1 = faux ;
'REPETER' bloc0 ( dim10 - 1 ) ;
i10 = &bloc0 ;
depl1 = 'EXTR' depl2 i10 ;
depl11 = 'EXTR' depl12 i10 ;
*
'SI' (depl1 'NEG' 0. ) ;
err_e0 = 'ABS' ( ( depl1 - depl11 ) / depl1 ) ;
err_e0 = err_e0 * 100. ;
'SINON' ;
err_e0 = 0. ;
'FINSI' ;
*
*
'SI' ( err_e0 '>' 3.E-1 ) ;
prob0 = vrai ;
'SINON' ;
prob0 = faux ;
'FINSI' ;
'SI' (prob0 'EGA' vrai ) ;
prob1 = vrai ;
'FINSI' ;
*
'FIN' bloc0 ;
*
'SI' ( prob1 'EGA' vrai ) ;
'ERRE' 5 ;
'SINON' ;
'ERRE' 0 ;
'FINSI' ;
*
*
'FIN' ;
Test ohno2 Comments
MOD0 = MODE VOL1 MECANIQUE ELASTIQUE ISOTROPE
VISCOPLASTIQUE OHNO ;
MAT0 = MATE MOD0
YOUN 7.34E10 NU 0.33
RHO 7.8E3 ALPHA 1.E-5
N 24 KK 10.E6 K0 116.E6
ALFK 1.5 ALFR 0.35 ALF 2.E6
A1 67.5E6 C1 1300 BET1 4807.E6 R1 4
A2 80.E6 C2 45 BET2 58480.E6 R2 4
PHI 1. B 12 GAMA 2.E-7 M 2
QMAX 455.E6 QSTA 200.E6 MU 19
ETA 0.06 EXP1 2. EXP2 2. ;
The Ohno model is close to the Chaboche viscoplastic one.
The equations for this model are as follows: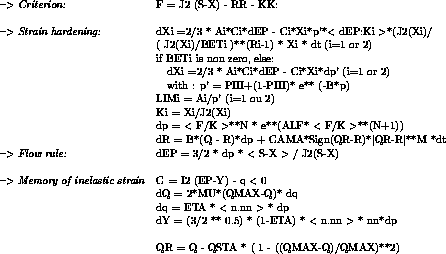
The initial value of Q is Q0 and must be initialized:
Q = Q0 = 30 MPa (steel 316). For this purpose, a field
of internal variables must be created, with a component
named 'QQ' , its value being Q0. This field will be
passed into the table of PASAPAS.
The parameter values for the steel 316L at 600°C are given for
information only. The data to be input are the following:

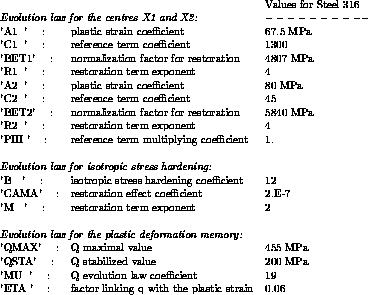
The following parameters will have to be specified with the elastic
behavior.
