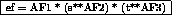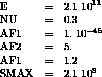
Test name
norton_cis1
Calculation type
ISOTROPIC ELASTIC MECHANICS - 2D - PLANE STRAIN
Finite element type
QUA4
Topic
Norton creep model for shear stresses.
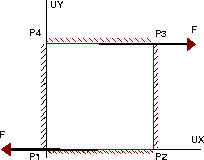
The structure is a square plate subjected to
shear stress (imposed load). It is embedded
at each side. The plate follows Norton creep model.
Goal
Test the Norton model for solid plates.
Version
97' customer version
Model description
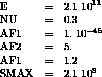
Test norton_cis1 Results
CASTEM FIGURES
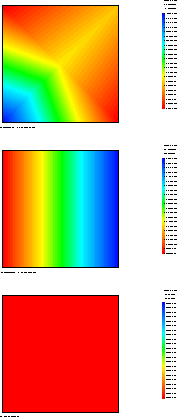
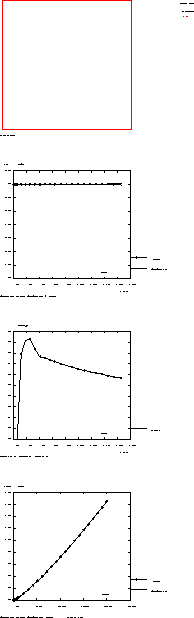
* Test Norton_cis1.dgibi: Jeux de données *
* --------------------------------------- *
* *
*
**************************************************
* *
* TEST DE VALIDATION D'UNE LOI DE COMPORTEMENT *
* -------------------------------------------- *
* DE MATERIAU *
* ----------- *
* *
* LOI DE COMPORTEMENT DE FLUAGE DE : *
* NORTON *
* *
* TEST POUR DES ELEMENTS MASSIFS *
* ------------------------------ *
* *
* MAILLAGE: *
* UNE PLAQUE CARREE DE COTE L=1 M *
* *
* CHARGEMENT: *
* CISAILLEMENT PUR *
* FORCES IMPOSEES *
* DEFORMATIONS PLANES *
* *
**************************************************
opti echo 0 dime 2 elem qua4 ;
*
* Maillage
*
p1 = 0. 0. ;
p2 = 1. 0. ;
p3 = 1. 1. ;
p4 = 0. 1. ;
li1 = d p1 1 p2 ;
li2 = d p2 1 p3 ;
li3 = d p3 1 p4 ;
li4 = d p4 1 p1 ;
mail1 = 'SURF' ( li1 'ET' li2 'ET' li3 'ET' li4 ) 'PLAN' ;
*
* Modele
*
AF1 = 1.E-45 ;
AF2 = 5. ;
AF3 = 1.2 ;
SMAX = 2.1E8 ;
youn0 = 2.1E11 ;
nu0 = .3 ;
mod0 = 'MODE' mail1 'MECANIQUE' 'ELASTIQUE' 'ISOTROPE'
'FLUAGE' 'NORTON' ;
mat0 = 'MATE' mod0 'YOUN' youn0 'NU' nu0 'AF1' AF1
'AF2' AF2 'AF3' AF3 'SMAX' SMAX ;
*
* Conditions aux limites
*
cl1 = 'BLOQ' mail1 'UY' ;
cl2 = 'BLOQ' li1 'UX' ;
cl0 = cl1 'ET' cl2 ;
*
* Chargement
*
depmax = 7.E7 ;
*chp1 = 'COOR' 2 mail1 ;
*chp1 = chp1 * depmax / 1. ;
*chp1 = 'NOMC' chp1 'UX' ;
*titr ' Champ de forces impose' ;
*trace chp1 mail1 ;
*chp2 = 'MANU' 'CHPO' mail1 1 'UY' 0. ;
*chp0 = chp1 + chp2 ;
dep1 = 'FORCE' li1 'FX' ( -1. * depmax ) 'FY' 0. ;
dep2 = 'FORCE' li3 'FX' depmax 'FY' 0. ;
dep0 = dep1 'ET' dep2 ;
ev0 = 'EVOL' 'MANU' temps ( 'PROG' 0. 1.E-4 1000. )
y ( 'PROG' 0. 1. 1. ) ;
cha0 = 'CHAR' 'MECA' dep0 ev0 ;
*
dt0 = .020 ;
dt1 = 2. * dt0 ;
dt2 = 5. * dt1 ;
dt3 = 5. * dt2 ;
tfin0 = 20. ;
*
* Appel à PASAPAS
*
ta1 = 'TABLE' ;
ta1 .'MODELE' = mod0 ;
ta1 .'CARACTERISTIQUES' = mat0 ;
ta1 .'CHARGEMENT' = cha0 ;
ta1 .'BLOCAGES_MECANIQUES' = cl0 ;
ta1 .'TEMPS_CALCULES' = ( 'PROG' 0. 'PAS' 1.E-4 2.E-4 ) 'ET'
( 'PROG' 3.E-4 'PAS' dt0 dt0 ) 'ET'
( 'PROG' ( dt0 + dt0 ) 'PAS' dt0 dt1 ) 'ET'
( 'PROG' ( dt1 + dt0 ) 'PAS' dt1 dt2 ) 'ET'
( 'PROG' ( dt2 + dt1 ) 'PAS' dt2 dt3 ) 'ET'
( 'PROG' ( dt3 + dt2 ) 'PAS' dt3 tfin0 ) ;
*
PASAPAS ta1 ;
*
* Post traitement
*
dim0 = 'DIME' ta1 .'TEMPS' ;
eps10 = 'PROG' 0. ;
sigm10 = 'PROG' 0. ;
def10 = 'PROG' 0. ;
def_th2 = 'PROG' 0. ;
sig_th2 = 'PROG' 0. ;
err_e2 = 'PROG' 0. ;
err_s2 = 'PROG' 0. ;
temp2 = 'PROG' 0. ;
rac0 = ( 3. ) ** ( .5 ) ;
H0 = youn0 / ( 2. * ( 1. + nu0 ) ) ;
*
prob0 = vrai ;
'REPETER' bloc0 ( dim0 - 1 ) ;
i1 = &bloc0 ;
*
* Résultats calculés
*
def0 = ta1 .'DEFORMATIONS_INELASTIQUES'.i1 ;
depl0 = ta1 .'DEPLACEMENTS'.i1 ;
sigm0 = ta1 .'CONTRAINTES'.i1 ;
temp0 = ta1 .'TEMPS'.i1 ;
var0 = ta1 .'VARIABLES_INTERNES'.i1 ;
eps0 = 'EPSI' mod0 depl0 ;
eps1 = 'EXTR' ( 'EXCO' eps0 'GAXY' 'SCAL' ) 'SCAL' 1 1 1 ;
sigm1 = 'EXTR' ( 'EXCO' sigm0 'SMXY' 'SCAL' ) 'SCAL' 1 1 1 ;
def1 = 'EXTR' ( 'EXCO' def0 'GIXY' 'SCAL' ) 'SCAL' 1 1 1 ;
eps10 = eps10 'ET' ( 'PROG' eps1 ) ;
sigm10 = sigm10 'ET' ( 'PROG' sigm1 ) ;
sigeq0 = 'VMIS' sigm0 mod0 ;
sigeq1 = 'EXTR' sigeq0 'SCAL' 1 1 1 ;
def10 = def10 'ET' ( 'PROG' def1 ) ;
temp2 = temp2 'ET' ( 'PROG' temp0 ) ;
var1 = 'EXTR' ( 'EXCO' var0 'EPSE' 'SCAL' ) 'SCAL' 1 1 1 ;
sig0 = 'CHAN' 'CHPO' eps0 mod0 ;
sigx = 'EXCO' sig0 'EPXX' ;
sigy = 'EXCO' sig0 'EPYY' ;
sigxy = 'EXCO' sig0 'GAXY' ;
*titr ' Contraintes suivant X' ;
*trace sigx mail1 ;
*titr ' Contraintes suivant Y' ;
*trace sigy mail1 ;
*titr ' Contraintes de cisaillement' ;
*trace sigxy mail1 ;
*
* Résultats analytiques
*
y2 = ( ( rac0 * depmax ) ** ( AF2 ) ) ;
y2 = y2 * ( temp0 ** AF3 ) ;
x2 = y2 * AF1 * rac0 ;
*
def_th1 = x2 ;
sig_th1 = H0 * ( eps1 - x2 ) ;
*
def_th2 = def_th2 'ET' ( 'PROG' def_th1 ) ;
sig_th2 = sig_th2 'ET' ( 'PROG' sig_th1 ) ;
*mess ' sig calculée =' sigm1 ;
*mess ' sig theorique =' sig_th1 ;
*mess ' def calculée =' def1 ;
*mess ' def théorique =' def_th1 ;
*
* Erreurs
*
'SI' ( def1 '>' ( 1.E-1 * eps1 ) ) ;
err_e1 = ( 'ABS' ( def1 - def_th1 ) ) / def1 ;
err_e1 = err_e1 * 100. ;
'SINON' ;
err_e1 = 0. ;
'FINSI' ;
'SI' ( sigm1 '>' 0. ) ;
err_s1 = ( 'ABS' ( sigm1 - sig_th1 ) ) / sigm1 ;
err_s1 = err_s1 * 100. ;
'SINON' ;
err_s1 = 0. ;
'FINSI' ;
*
'SI' ( ( err_e1 '>' .25 ) 'OU' ( err_s1 '>' .25 ) ) ;
prob0 = faux ;
mess 'err_e1 err_s1' err_e1 err_s1 ;
'FINSI' ;
err_e2 = err_e2 'ET' ( 'PROG' err_e1 ) ;
err_s2 = err_s2 'ET' ( 'PROG' err_s1 ) ;
*
'MESS' ' Fin du calcul de restitution au temps ' temp0 ;
*mess ' ' ;
*
'FIN' bloc0 ;
*
defo0 = 'DEFO' mail1 depl0 0. ;
defo1 = 'DEFO' mail1 depl0 1. 'ROUG' ;
*titr ' deformee finale' ;
*trace ( defo0 'ET' defo1 ) ;
*
'SI' ( prob0 'EGA' faux ) ;
'ERRE' 5 ;
'SINON' ;
'ERRE' 0 ;
'FINSI' ;
*
* Tracés
*
evo1 = 'EVOL' 'MANU' 'epsp' def10 'sigm' sigm10 ;
evo2 = 'EVOL' 'MANU' 'epsp' def_th2 'sigm' sig_th2 ;
evo3 = 'EVOL' 'MANU' 'epsp' def10 'erreur_%' err_e2 ;
evo4 = 'EVOL' 'MANU' 'epsp' def10 'erreur_%' err_s2 ;
evo5 = 'EVOL' 'MANU' 'temps' temp2 'epsp' def10 ;
evo6 = 'EVOL' 'MANU' 'temps' temp2 'epsp' def_th2 ;
TAB = 'TABLE' ;
TAB. 1 = 'MARQ CROI ' ;
TAB. 2 = 'MARQ PLUS ' ;
TAB.'TITRE' = 'TABLE' ;
TAB.'TITRE'. 1 = MOT 'CALCUL' ;
TAB.'TITRE'. 2 = MOT 'THEORIE' ;
*'DESSIN' ( evo1 'ET' evo2 )
*'TITR' ' Comparaison calcul theorie'
*'LEGE' TAB ;
TAB = 'TABLE' ;
TAB. 1 = 'MARQ CROI ' ;
*TAB. 2 = 'MARQ PLUS ' ;
TAB.'TITRE' = 'TABLE' ;
TAB.'TITRE'. 1 = MOT 'DEFORMATION' ;
*TAB.'TITRE'. 2 = MOT 'CONTRAINTE' ;
*'DESSIN' ( evo3 )
*'TITR' ' Evolution des erreurs (en pourcentage) '
*'LEGE' TAB ;
TAB = 'TABLE' ;
TAB. 1 = 'MARQ CROI ' ;
TAB. 2 = 'MARQ PLUS ' ;
TAB.'TITRE' = 'TABLE' ;
TAB.'TITRE'. 1 = MOT 'CALCUL' ;
TAB.'TITRE'. 2 = MOT 'THEORIE' ;
*'DESSIN' ( evo5 'ET' evo6 )
*'TITR' ' Comparaison calcul theorie, deformation-temps'
*'LEGE' TAB ;
*
'FIN' ;
Test norton_cis1 Comments
MOD0 = MODE MAIL1 MECANIQUE ELASTIQUE ISOTROPE
FLUAGE NORTON ;
MAT0 = MATE MOD0 YOUN YOUN0 NU NU0 'AF1' AF1
'AF2' AF2 'AF3' AF3 'SMAX' SMAX ;
Several creep models are available in CASTEM2000.
In each case we have to specify the elastic
behavio,r the equivalent creep deformation (ef),
the equivalent stress (s) and the time (t).