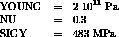
Test name
plas6
Calculation type
MECHANICS ELASTIC PLASTIC - PLANE STRESS
Finite element type
QUA4
Topic
Rectangle subjected to pure bending.
A rectangle is embedded from two adjacent sides.
Linear imposed displacements are applied to one
side. Calculations are performed for plane stresses and
with a pure plastic model.
Goal
Calculate the pure bending moment along the side
where the displacements are applied.
Reference CASTEM
R. Hill, Mathematical theory of plasticity, Oxford,
Oxford Clavendon Press, 1950.
Test V.P.C.S. numero SSNP11/89
Version
97' customer version
Model description
Elastic and pure plastic material
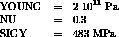
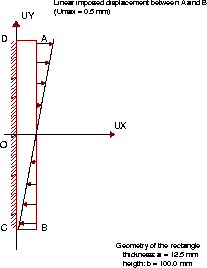
Test plas6 Results
CASTEM FIGURES


* Test Plas6.dgibi: Jeux de données *
* --------------------------------- *
* *
* CAS TEST DU 91/07/23 PROVENANCE : BIRET
SAUT PAGE;
*
*******************************************************
* *
* TEST PLAS6 *
* *
* RECTANGLE EN FLEXION PURE (CONTRAINTES PLANES, *
* PLASTICITE PARFAITE) *
* *
* Test V.P.C.S. numero SSNP11/89 *
* *
* References : R. Hill, Mathematical theory of *
* plasticity, Oxford, Oxford Clavendon Press, 1950. *
* *
* Description : *
* ----------- *
* *
* axe y *
* D | A *
* |----- ---- UA epaisseur a = 12.5 mm *
* | | / hauteur b = 100.0 mm *
* | | / *
* | | / *
* | |/ *
* O |-----/-----> axe x *
* | /| *
* | / | *
* | / | *
* | / | *
* ----- *
* C UB B *
* *
* Chargement : Deplacement impose variant *
* lineairement de UA a -UA entre A et B, *
* UA croissant jusqu'a : UAmax = 0.5 mm . *
* *
* Conditions aux limites : *
* sur CD : u = 0. *
* au point O : v = 0. *
* *
* Proprietes des materiaux : *
* Materiau elastique, parfaitement plastique *
* E = 210 000 MPa , NU = 0.3 , SIGY = 483 MPa *
* *
*******************************************************
*
OPTI ECHO 1;
*
OPTI DIME 2;
OPTI MODE PLAN CONT;
OPTI ELEM QUA4;
OPTI ISOV LIGNE;
*
GRAPH = 'N';
GRAPH2 = 'N';
*
TEMPS;
*******************************************************
* geometrie : maillage *
*******************************************************
*
PA = 12.5E-3 50.E-3;
PB = 12.5E-3 -50.E-3;
PC = 0. -50.E-3;
PD = 0. 50.E-3;
*
NB1 = 32; NB2 = 4;
D1 = PA DROI NB1 PB;
D2 = PB DROI NB2 PC;
D3 = PC DROI NB1 PD;
D4 = PD DROI NB2 PA;
*
SUR1 = DALL D1 D2 D3 D4 PLAN;
*
SI (NEG GRAPH 'N');
TITR 'PLAS6 : MAILLAGE';
TRAC QUAL SUR1;
FINSI;
*
NBNO1 = NBNO SUR1;
NBEL1 = NBEL SUR1;
*
*******************************************************
* calcul du modele,caracteristiques *
*******************************************************
*
MOD1 = MODL SUR1 MECANIQUE ELASTIQUE PLASTIQUE
PARFAIT QUA4;
MAT1 = MATR MOD1 YOUN 2.1E11 NU 0.3 SIGY 483.E6;
*
*******************************************************
* conditions aux limites *
*******************************************************
*
CL1 = BLOQ UX D3;
CL2 = BLOQ UY (SUR1 POIN PROC (0. 0.));
CL3 = BLOQ UX D1;
CL = CL1 ET CL2 ET CL3;
*
* Creation du chpoint de deplacement impose variable :
* deplacement impose variant lineairement de u a -u
* entre A et B, u croissant jusqu'a 0.5 mm .
*
I = 0.;
LISD1 = PROG 1.;
REPETER BLOC10 NB1;
I = I + 1.;
YY = 1. - (2. * (I / NB1));
LISD1 = LISD1 ET (PROG YY);
FIN BLOC10;
*
LISD1 = LISD1 * 1.E-3;
CHPO1 = MANU CHPO D1 1 UX LISD1;
*
CHA1 = DEPI CL3 CHPO1;
*
*******************************************************
* objets relatifs a la procedure PASAPAS *
*******************************************************
*
TAB1 = TABLE;
*
*On prend comme liste des pseudo-temps le deplacement u
*
LREEL1= PROG 0.02875 0.05 0.1 0.15 0.2 0.3 0.4 0.5 1.0;
*
* Chargement
*
EVOL1 = EVOL MANU UA LREEL1 COEFF LREEL1;
CHAR1 = CHAR DIMP CHA1 EVOL1;
*
*******************************************************
* resolution *
*******************************************************
*
TAB1.'CARACTERISTIQUES' = MAT1;
TAB1.'CHARGEMENT' = CHAR1;
TAB1.'MODELE' = MOD1;
TAB1.'TEMPS_CALCULES' = LREEL1;
TAB1.'BLOCAGES_MECANIQUES' = CL;
PASAPAS TAB1;
*
*******************************************************
* extraction des resultats *
*******************************************************
*
* Initialisation
*
MOM1 = TABLE;
LISD2 = LISD1 * 50.;
MOM2 = TABLE;
ERG = TABLE;
*
MOM2.1 = 805.0; MOM2.2 = 1074.;
MOM2.3 = 1174.; MOM2.4 = 1193.;
MOM2.5 = 1199.; MOM2.6 = 1204.;
MOM2.7 = 1205.; MOM2.8 = 1206.;
MOM2.9 = 1207.5;
*
*Boucle pour chaque pas de chargement : fonction de UA.
*
I = 0;
REPETER BLOC1 9;
I = I + 1;
CONT1 = TAB1.CONTRAINTES.I;
DEPL1 = TAB1.DEPLACEMENTS.I;
*
* Passage du champs de contrainte en chpoints
* (utilisation des nouveaux chamelems)
*
CHPO10 = CHAN CHPO MOD1 CONT1;
*
* Trace facultatif de la repartition
* de la contrainte SMXX
*
SI (I EGA 9);
SI (NEG GRAPH2 'N');
TITR 'PLAS6 : CONTRAINTE SMXX';
BB = EXCO 'SMXX' CONT1;
TRAC BB SUR1;
FINSI;
FINSI;
*
* Trace facultatif de la deformee
* (verification du chargement)
*
SI (I EGA 9);
SI (NEG GRAPH2 'N');
TITR 'PLAS6 : DEFORMEE';
DEF0 = DEFO SUR1 DEPL1 0.;
DEF1 = DEFO SUR1 DEPL1 2. VERT;
TRACE SUR1 (DEF0 ET DEF1);
FINSI;
FINSI;
*
* Calcul du moment de flexion du aux contraintes
* smxx s'exercant le long de AB.
*
LIST2 = PROG;
J = 0;
NB = NB1 + 1;
REPETER BLOC4 NB;
J = J + 1;
D = EXTR LISD2 J;
POI1 = SUR1 POIN PROC (12.5E-3 D);
SM = EXTRA CHPO10 SMXX POI1;
LIST2 = LIST2 ET (PROG SM);
FIN BLOC4;
*
LIST3 = LIST2 * LISD2;
TITR 'CONTRAINTE SMXX';
ESMXX = EVOL MANU Y LISD2 SMXX LIST2;
TITR 'PRODUIT Y * SMXX';
EYSMXX = EVOL MANU Y LISD2 YSMXX LIST3;
*
SI (I EGA 9);
SI (NEG GRAPH2 'N');
DESSIN ESMXX;
DESSIN EYSMXX;
FINSI;
FINSI;
MOM1.I = SOMME EYSMXX;
MOM1.I = EXTR MOM1.I 1;
*
MOM1.I = -1.E-3 * MOM1.I;
*
ERG.I = 100. * (ABS ((MOM1.I - MOM2.I) / MOM2.I));
*
FIN BLOC1;
*
*******************************************************
* affichage des resultats *
*******************************************************
*
MESS 'RESULTATS : PLAS6';
MESS '-------------------';
SAUT LIGN;
*
MESS 'Moment de flexion du aux contraintes SMXX
le long de AB.';
MESS '--------------------------------------------------------';
SAUT LIGN;
*
MESS ' UAmax = 0.02875 mm :';
MESS ' ------------------';
MESS ' Moment theorique :' MOM1.1 'N.m';
MESS ' Moment calcule :' MOM2.1 'N.m';
MESS ' Soit un ecart de :' ERG.1 '%';
SAUT LIGN;
*
MESS ' UAmax = 0.05 mm :';
MESS ' --------------- ';
MESS ' Moment theorique :' MOM1.2 'N.m';
MESS ' Moment calcule :' MOM2.2 'N.m';
MESS ' Soit un ecart de :' ERG.2 '%';
SAUT LIGN;
*
MESS ' UAmax = 0.1 mm :';
MESS ' --------------';
MESS ' Moment theorique :' MOM1.3 'N.m';
MESS ' Moment calcule :' MOM2.3 'N.m';
MESS ' Soit un ecart de :' ERG.3 '%';
SAUT LIGN;
*
MESS ' UAmax = 0.15 mm :';
MESS ' ---------------';
MESS ' Moment theorique :' MOM1.4 'N.m';
MESS ' Moment calcule :' MOM2.4 'N.m';
MESS ' Soit un ecart de :' ERG.4 '%';
SAUT LIGN;
*
MESS ' UAmax = 0.2 mm :';
MESS ' --------------';
MESS ' Moment theorique :' MOM1.5 'N.m';
MESS ' Moment calcule :' MOM2.5 'N.m';
MESS ' Soit un ecart de :' ERG.5 '%';
SAUT LIGN;
*
MESS ' UAmax = 0.3 mm :';
MESS ' --------------';
MESS ' Moment theorique :' MOM1.6 'N.m';
MESS ' Moment calcule :' MOM2.6 'N.m';
MESS ' Soit un ecart de :' ERG.6 '%';
SAUT LIGN;
*
MESS ' UAmax = 0.4 mm :';
MESS ' --------------';
MESS ' Moment theorique :' MOM1.7 'N.m';
MESS ' Moment calcule :' MOM2.7 'N.m';
MESS ' Soit un ecart de :' ERG.7 '%';
SAUT LIGN;
*
MESS ' UAmax = 0.5 mm :';
MESS ' --------------';
MESS ' Moment theorique :' MOM1.8 'N.m';
MESS ' Moment calcule :' MOM2.8 'N.m';
MESS ' Soit un ecart de :' ERG.8 '%';
SAUT LIGN;
*
MESS ' UAmax = 1.0 mm :';
MESS ' --------------';
MESS ' Moment theorique :' MOM1.9 'N.m';
MESS ' Moment calcule :' MOM2.9 'N.m';
MESS ' Soit un ecart de :' ERG.9 '%';
SAUT LIGN;
*
MESS 'Donnees sur le maillage';
MESS '-----------------------';
MESS ' Nombre d elements :' NBEL1 'QUA4';
MESS ' Nombre de noeuds :' NBNO1 ;
SAUT LIGN;
*
*******************************************************
* code fonctionnement *
*******************************************************
*
ERGMAX = MAXI (PROG ERG.1 ERG.2 ERG.3 ERG.4 ERG.5 ERG.6
ERG.7 ERG.8 ERG.9);
*
SI (ERGMAX <EG 5.);
ERRE 0;
SINON;
ERRE 5;
FINSI;
SAUT LIGN;
*
TEMPS;
*
FIN;
*