Les principales méthodes de discrétisation des équations de
Navier-Stokes sont dans le jeu de données associé au TP
d'aujourd'hui. Nous allons passer en revue la manière de coder
dans CAST3M ces différentes méthodes ainsi que les éléments finis
en vitesse/pression associés. On consultera le cours associé à ce
TP pour plus de détails sur ces algorithmes. La variable IRESO (resp. ICHOI) pilote le choix de l'algorithme (resp.
de l'élément fini en vitesse/pression). L'inconnue en température
est discrétisée dans le même espace que la vitesse.
Les algorithmes de résolution
Algorithme implicite : Les équations en vitesse, pression
et température sont discrétisées et résolues simultanément.
Méthode de projection semi-explicite : Les équations en vitesse, pression et
température sont découplées : elles sont au sein d'un pas de temps résolues les
unes après les autres. L'équation de quantité de mouvement est résolue
explicitement si bien que le schéma est stable sous conditions -- le pas de
temps est limité par des contraintes de stabilités linéaires (conditions sur le
nombre CFL et le nombre de Fourier). La pression est solution d'un
pseudo-Laplacien. La température est aussi résolue explicitement. L'algorithme semi-explicite est la variante la plus explicite des méthodes de
projection.
Méthode de projection semi-implicite : Les équations en vitesse, pression
et température sont, comme précédemment, découplées. Cependant, elles sont
résolues par une approche implicite. De ce fait, le pas de temps n'est pas
soumis à des contraintes de stabilités linéaires. Pour obtenir une solution
physique aux équations découplées, il doit cependant rester dans des limites
raisonnables.
Mise en oeuvre dans CAST3M
Pour décrire le système d'équation, on utilise comme pour la description d'une
équation scalaire l'opérateur EQEX. Après avoir créé le maillage du
domaine de calcul et le modèle Navier-Stokes associé -- cf les deux premiers
TP -- on précise dans EQEX un certain nombre de paramètres. Pour cela,
on fixe une valeur après un mot clef :
- ITMA : Nombre de pas de temps (type ENTIER)
-- ce champ est intéressant lorsque le pas de
temps est calculé automatiquement afin d'éviter les calculs sans
fin ;
- NITER : Nombre d'itérations de point fixe à réaliser
à chaque pas de temps (type ENTIER) -- à n'utiliser que dans le
cas de problème non linéaire (mettre à 1 sinon) ;
- OMEGA : Coefficient de relaxation utilisé dans le
cas d'itérations de point fixe (type FLOTTANT) -- à n'utiliser
que dans le cas où on réalise un point fixe (mettre à 1. dans le
cas où NITER=1) ;
- FIDT : Fréquence d'impression des informations sur le
listing (type ENTIER) ;
- ALFA : Abusivement appelé CFL, ce paramètre multiplie
le pas de temps de stabilité trouvé par le code (type FLOTTANT)
-- utilisé uniquement lorsque le pas de temps n'est pas imposé
par l'utilisateur (voir la notice de l'opérateur DFDT).
- TFINAL : Fixe la valeur maximale de la chronologie
au delà de laquelle le calcul s'arrête (type FLOTTANT).
Ainsi dans l'exemple suivant :
- RV = 'EQEX' DOMTOT 'ITMA' 500 'NITER' 1
'OMEGA' 1. 'FIDT' 5000
on va résoudre un problème décrit sur le domaine DOMTOT
pendant 500 pas de temps sans réaliser d'itérations de point fixe.
On limite le volume des impressions sur le listing du calcul en
donnant à FIDT une valeur supérieure à ITMA.
Pour décrire les équations, on opère aussi comme dans le cas de la
résolution du problème de transport d'un champ scalaire passif par
diffusion et convection. On appelle les opérateurs associés à
chacun des monomes des équations :
-
- On choisit de nommer l'inconnue de vitesse
'UN', l'inconnue de pression 'PRES' et l'inconnue de
température 'TN'.
-
- On discrétise l'équation de quantité de
mouvement via l'opérateur 'NS'. Les arguments de cet
opérateur sont le coefficient de viscosité cinématique
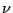 (coefficient devant le monome
(coefficient devant le monome
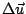 qui correspond à
qui correspond à
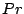 dans la forme adimensionnée des équations), le
``coefficient'' de flottabilité
dans la forme adimensionnée des équations), le
``coefficient'' de flottabilité
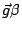 (correspond au
vecteur (0, -
(correspond au
vecteur (0, - 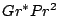 )), le nom de l'inconnue de température
(ici ''TN') et enfin la valeur de la température de
référence en adimensionné (ici 0.) soit :
)), le nom de l'inconnue de température
(ici ''TN') et enfin la valeur de la température de
référence en adimensionné (ici 0.) soit :
- 'ZONE' DOMTOT 'OPER' 'NS' NU GB 'TN' 0. 'INCO' 'UN'
- avec NU=Pr ; GB=0. (-1.*Gr*Pr*Pr).
- Les trois derniers arguments de l'opérateur NS modélisent le
terme de flottabilité. Dans le cas où on ne s'interesse qu'à la résolution
des équations de Navier-Stokes, sans effet thermique, donc sans terme de
flottabilité, l'opérateur NS a un ou deux arguments (la viscosité
cinématique et un éventuel terme source).
-
- On discrétise l'équation de transport du champ de
température en utilisant soit l'opérateur TSCAL (transport d'un champ
scalaire), soit les opérateurs LAPN, KONV et FIMP : ils
discrétisent le terme diffusif, le terme convectif et le terme source. Les
arguments de l'opérateur TSCAL sont le coefficient de diffusion, le
champ de vitesse et le terme source. L'argument de l'opérateur LAPN est
le coefficient de diffusion (ici 1.). Les trois arguments de l'opérateur KONV sont un coefficient multiplicateur (ici 1.), le nom du champ de
vitesse (ici 'UN') et le coefficient de diffusion afin de pouvoir si on
le souhaite décentrer le schéma numérique (méthode 'SUPG' par exemple).
L'argument de l'opérateur FIMP est la densité de source de chaleur (ici
1.) :
- 'ZONE' DOMTOT 'OPER' 'TSCAL' ALFA 'UN' Q 'INCO' 'TN'
- ou
- 'ZONE' DOMTOT 'OPER' 'LAPN' ALFA 'INCO' 'TN'
- 'ZONE' DOMTOT 'OPER' 'KONV' COEF 'UN' ALFA 'INCO'
'TN'
- 'ZONE' DOMTOT 'OPER' 'FIMP' Q 'INCO' 'TN'
- avec ALFA=1. ; Q=1. ; COEF=1. ;
-
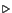
- On discrétise les termes en pression dans un troisième
temps. L'opérateur KBBT discrétise le terme en gradient de pression de
l'équation de quantité de mouvement (terme qui n'est pas discrétisé par
l'opérateur NS) ainsi que le terme en divergence
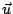 . Dans un
contexte de résolution implicite, c'est cet opérateur qui couple les
inconnues de vitesse et de pression. En méthode de projection, les matrices
associées aux opérateurs gradient et divergence -- l'une est la transposée
de l'autre d'où le nom de l'opérateur -- permettent d'évaluer le
pseudo-laplacien en pression. L'argument de cet opérateur est un éventuel
coefficient multiplicateur. Ce coefficient vaut 1. si l'opérateur est appelé
en implicite et -1. sinon.
. Dans un
contexte de résolution implicite, c'est cet opérateur qui couple les
inconnues de vitesse et de pression. En méthode de projection, les matrices
associées aux opérateurs gradient et divergence -- l'une est la transposée
de l'autre d'où le nom de l'opérateur -- permettent d'évaluer le
pseudo-laplacien en pression. L'argument de cet opérateur est un éventuel
coefficient multiplicateur. Ce coefficient vaut 1. si l'opérateur est appelé
en implicite et -1. sinon.
- 'ZONE' DOMTOT 'OPER' 'KBBT' C1 'INCO' 'UN' 'PRES'
- avec C1=1. en implicite et -1. en explicite.
Les espaces de discrétisation
Le choix des espaces de discrétisation se fait en deux étapes. On
indique dans l'objet modèle Navier-Stokes l'espace de
discrétisation choisi pour les inconnues autres que la vitesse. On
dispose des choix suivants :
- LINE : Les espaces d'approximation sont
linéaires (éléments dits P1 et Q1) ;
- MACRO : Les éléments linéaires sont stabilisés par
la technique des macro-éléments, les espaces d'approximation étant
linéaires sur chaque micro-élément ;
- QUAF : Les espaces d'approximation sont
quadratiques (éléments dits P2 et Q2).
On indique l'espace de discrétisation de la pression après la directive OPTI de l'opérateur EQEX afin que les opérateurs de discrétisation
puissent travailler :
- CENTRE : La pression est constante sur chaque
élément ;
- CENTREP1 : La pression est linéaire sur chaque
élément et discontinue d'un élément à ses voisins ;
- MSOMMET : La pression est linéaire sur chaque
élément et continue d'un élément à ses voisins.
Comme nous l'avons vu en cours, tous les couples
vitesse/pression ne sont pas judicieux. Cinq possibilités
vous sont offertes via la variable ICHOI :
- LINE et CENTRE : Cet élément est le plus simple mais sujet
aux modes de pression parasites.
- MACRO et CENTRE : Cet élément est la version stabilisée de
l'élément précédant.
- MACRO et CENTREP1 : Cet élément est stable dans le cas de
quadrangles linéaires. Pour les triangles, il faudrait ajouter la bulle.
- QUAF et CENTREP1 : En augmentant le degré d'approximation en
vitesse on gagne en précision mais au prix d'un temps de calcul plus
important. En effet, le couplage entre les degrés de liberté en vitesse
augmente d'où des matrices moins creuses qu'en linéaire.
- LINE et MSOMMET : Bien que sujet aux modes de pression
parasites, cet élément permet d'approximer linéairement et continuement
vitesses et presions pour un coût raisonnable.
- QUAF et MSOMMET : Pour ceux qui souhaitent de la stabilité,
de la précision et des pressions continues. A noter que par rapport au choix
CENTREP1, le choix MSOMMET diminue la taille du problème en
pression (continuité des pressions).
Les couples LINE/CENTREP1 et QUAF/CENTRE sont sans
objets.
Le mot clef associé à l'espace de discrétisation en vitesse est un des
arguments du modèle Navier-Stokes. Il sert aussi à indiquer l'espace de
discrétisation des inconnues autres que la pression, ici la température.
Celui associé à la pression intervient dans les options de l'opérateur KBBT.
ATTENTION : Tous les éléments vitesse/pression ne sont pas disponibles avec tous les
algorithmes. Ainsi, on se contentera d'éléments linéaires en semi-explicite
(i.e. pas de QUAF en semi-explicite); de pressions discontinues en
implicite (i.e. pas de MSOMMET en implicite). Un jour viendra ... peut-être.
Les conditions aux limites
Le domaine de calcul est fermé et axisymétrique. La composante
horizontale de la vitesse est donc nulle sur le contour du domaine
(axe de symétrie et contour extérieur) ; la composante verticale
est nulle sur le contour extérieur ; la température est égale à la
température de référence sur le contour extérieur. C'est -- comme
dans le cas scalaire -- la directive CLIM de l'opérateur
EQEX qui permet d'imposer les conditions aux limites.
Comme le domaine est fermée, il faut supprimer une équation du
système puisque la contrainte d'incompressibilité lie les
inconnues en vitesse. C'est pourquoi on fixe la pression à 0 en
un point du support de l'inconnue de pression.
Les utilitaires
Trois procédures utilisateurs sont fournies en tête du jeu de
données : courant, calcnuss et residu. Elles permettent
respectivement de calculer les lignes de courant, le nombre de
Nusselt et l'évolution du résidu en température durant le
transitoire. Cette dernière procédure est appelé à chaque pas de
temps et l'évolution du résidu en température est tracé à chaque
pas de temps.
Les autres procédures sont appelés au moment du post-traitement à
l'issue du calcul. En plus des lignes de courant et du Nusselt,
nous y post-traitons la température, la vitesse et la pression.
Les procédures utilisateurs et le post-traitement doivent souvent
être adaptés à la situation traitée, aux évolutions du code.
Ainsi, la procédure calcnuss peut être simplifié en
calculant directement le gradient de température au sommet
(nouvelle option GRADS de KOPS). C'est pourquoi il
vous appartient de comprendre les exemples fournis afin de pouvoir
les adapter à vos futurs travaux.
traduction
2003-11-04